实例复习机器学习数学 - 1. 事件与概率

Posted 2021-08-06 干货满满张哈希

从骰子实验引出的各种概率概念

1.投骰子，出现点数为 6 的概率 $\frac{1}{6}$. 投骰子，已知出现点数为偶数，出现点数为 6 的概率则是 $\frac{1}{3}$，这个概率即 条件概率。

2.条件概率为：假设我们知道 A 事件已经发生，在此基础上我们想知道 B 事件发生的概率，这个概率为条件概率，记作 $P(B|A)$

3.古典概率模型：假设一个实验，有 $\Omega$ 个等可能性的结果，事件 A 包含其中 $X$ 个结果，事件 B 包含其中 $Y$ 个结果，$Z$ 代表其中交叉的事件：

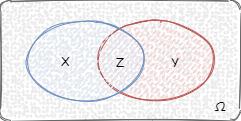
事件 A 发生的概率：$P(A)=\frac{X}{\Omega }$；事件 B 发生的概率：$P(B)=\frac{Y}{\Omega }$；事件 A、B 都发生的概率：$P(AB)=\frac{Z}{\Omega }$如果事件 A 已经发生，那么事件 B 也发生的概率是 $P(B|A)=\frac{Z}{X}$，将公式展开： 这个公式就是条件概率公式
$$P(B|A)=\frac{\frac{Z}{\Omega }}{\frac{X}{\Omega }}=\frac{P(AB)}{P(A)}$$

4.如果条件概率 $P(B|A)$ 大于 $P(B)$，代表事件 A 的发生会促进事件 B 的发生，例如上面投骰子的例子。还有可以看下图，本身 $P(B)$ 的概率是比较小的，在事件 A 已发生的情况下，由于相交部分较多，事件 B 发生的概率也提升了：

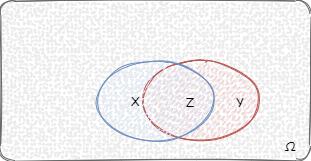
5.如果条件概率 $P(B|A)$ 小于 $P(B)$，代表事件 A 不会促进事件 B 的发生，例如事件 A 为投骰子点数为偶数，事件 B 为投骰子点数小于 < 4，事件 A 和 事件 B 发生的概率都为 $1/2$，事件 A、B 同时发生的概率是 $1/6$，条件概率 $P(B|A)$ 为 $1/3$。还有可以看下图，本身 $P(B)$ 的概率是比较大的，在事件 A 已发生的情况下，由于相交部分较少，事件 B 发生的概率被降低了：

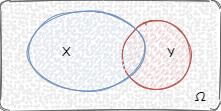
6.如果条件概率 $P(B|A)$ 等于 0，代表事件 A 与事件 B 完全不相交，即事件 A 发生则事件 B 一定不会发生，事件 A 与事件 B 是不相容事件，或者是互斥事件。如下图所示：

7.还有可能条件概率 $P(B|A)$ 等于 $P(B)$，在这种情况下其实就是事件 A、B 的发生互不相关，例如有两个骰子，事件 A 为骰子 1 投出点数 6，事件 B 为骰子 2 投出点数 2，事件 A 和 事件 B 发生的概率都为 $1/6$，那么事件 A、B 同时发生的概率是 $\frac{1}{36}$，条件概率 $P(B|A)$ 等于 $\frac{1}{6}$，我们一般称这种为独立事件。如下图所示：

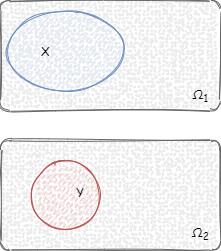
全概率公式与骰子实验验证

假设有 $A_1,A_2,...,A_n$ 这些互斥事件，包含了实验所有可能的结果：

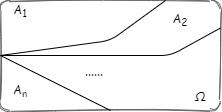
即有$P(A_1)+P(A_2)+...+P(A_n)=1$。拿刚刚的骰子举例，其实就是抛一次骰子，点数分别为 1，2，3，4，5，6.

假设再有一个事件 B，用古典概率表示如图：

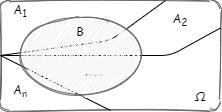
事件 B 的概率，可以通过事件 B 在 $A_1,A_2,...,A_n$ 这些互斥事件上的条件概率以及这些事件的概率进行计算，即全概率公式：
$$条件：P(A_1)+P(A_2)+...+P(A_n)=1$$
$$结果：P(B)=P(B\Omega )=P(B{A}_1)+P(B{A}_2)+...+P(B{A}_n)=P(A_1)P(B|A_1)+P(A_2)P(B|A_2)+...+P(A_n)P(B|A_n)$$
例如事件 B 就是投出的骰子为偶数，$P(B)=\frac{1}{2}$， P ( A 点 数 = 1 ) P ( B ∣ A 点 数 = 1 ) + P ( A 点 数

以上是关于实例复习机器学习数学 - 1. 事件与概率的主要内容，如果未能解决你的问题，请参考以下文章

机器学习数学基础 - 概率论

实例复习机器学习数学 - 2. 几种典型离散随机变量分布

机器学习数学基础总结

机器学习：2.机器学习相关数学基础

机器学习数学系列：机器学习与数学基础知识

2.机器学习相关数学基础