AtCoder Beginner Contest 205 E - White and Black Balls(卡特兰数变形)

Posted 2021-08-06 issue是fw

LINK

看到题目非常像卡特兰数,实际上就是

考虑以$(0,0)$为起点,选白球相当于往右下走一步,黑球相当于向右上走一步

白球$n$个,黑球$m$个,设$x=m-n$(先设$m>=n$)

放在坐标轴上,类似这样的一张图

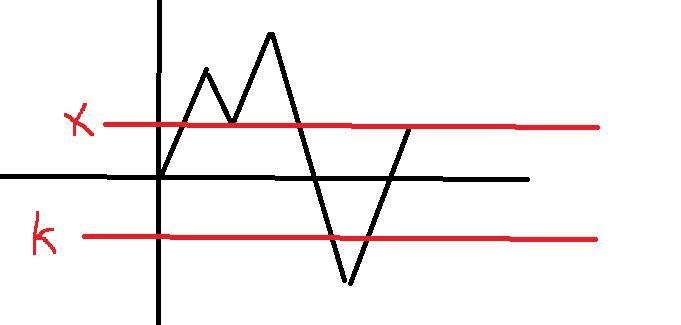
不管怎么走,最后终点都是$(n+m,x)$

总的方案是$\left(\genfrac{}{}{0ex}{}{n+m}{n}\right)$,我们需要知道不合法的方案是多少

容易看出,只要上面的折线越过了$y=-k$这根直线就不合法

我们构造另一条折现,以$y=-k-1$为对称轴翻转得到

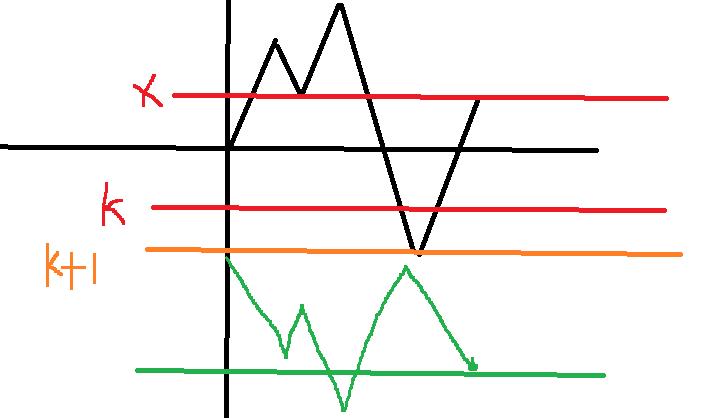
发现翻转后折线的终点变为$(n+m,2k+2+x)$

也就是不合法的方案数相当于向下走$z$步,满足$z-(n+m-z)=2k+2+x$

于是真正的方案数为$\left(\genfrac{}{}{0ex}{}{n+m}{n}\right)-\left(\genfrac{}{}{0ex}{}{n+m}{z}\right)$

当$n<m$时同理

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int mod = 1e9+7;
const int maxn = 2e6+10;
int n,m,k,fac[maxn];
int quick(int x,int n)
{
	int ans = 1;
	for( ; n ; n>>=1,x=x*x%mod )
		if( n&1 )	ans = ans*x%mod;
	return ans;
}
int C(int n,int m)
{
	if( n<m )	return 0ll;
	return fac[n]*quick( fac[m]*fac[n-m]%mod,mod-2 )%mod;
}
signed main()
{
	fac[0] = 1;
	for(int i=1;i<=2000000;i++)	fac[i] = fac[i-1]*i%mod;
	cin >> n >> m >> k;
	if( m+k<n )	puts("0");
	else
	{
		//满足m+k>=n
		int ans = 0;
		if( m>=n )
		{
			int x = m-n;
			int z = (2*k+2+x+n+m)/2;
			ans = C(n+m,m)-C(n+m,z);
		}
		else
		{
			int x = n-m;
			int z = (2*k+2-x+n+m)/2;
			ans = C(n+m,m)-C(n+m,z);	
		}
		cout << ( ans%mod+mod )%mod;
	}
}