leetcode LCP 07. 传递信息

Posted 2021-08-04 ZSYL

BFS&DFS&DP

• 题目描述
• DFS
• BFS
• DP

题目描述

小朋友 A 在和 ta 的小伙伴们玩传信息游戏，游戏规则如下：

1.有 n 名玩家，所有玩家编号分别为 0 ～ n-1，其中小朋友 A 的编号为 0
2.每个玩家都有固定的若干个可传信息的其他玩家（也可能没有）。传信息的关系是单向的（比如 A 可以向 B 传信息，但 B 不能向 A 传信息）。
3.每轮信息必须需要传递给另一个人，且信息可重复经过同一个人

给定总玩家数 n，以及按 [玩家编号,对应可传递玩家编号] 关系组成的二维数组 relation。返回信息从小 A (编号 0 ) 经过 k 轮传递到编号为 n-1 的小伙伴处的方案数；若不能到达，返回 0。

链接：https://leetcode-cn.com/problems/chuan-di-xin-xi

示例 1：

输入：n = 5, relation = [[0,2],[2,1],[3,4],[2,3],[1,4],[2,0],[0,4]], k = 3

输出：3

解释：信息从小 A 编号 0 处开始，经 3 轮传递，到达编号 4。共有 3 种方案，分别是 0->2->0->4， 0->2->1->4， 0->2->3->4。

DFS

可以把传信息的关系看成有向图，每个玩家对应一个节点，每个传信息的关系对应一条有向边。

如 x 可以向 y 传信息，则对应从节点 x 到节点 y 的一条有向边。

寻找从编号 0 的玩家经过 k 轮传递到编号 n−1 的玩家处的方案数，等价于在有向图中寻找从节点 0 到节点 n−1 的长度为 k 的路径数，同一条路径可以重复经过同一个节点。

可以使用深度优先搜索计算方案数。从节点 0 出发做深度优先搜索，每一步记录当前所在的节点以及经过的轮数，当经过 k 轮时，如果位于节点 n−1，则将方案数加 1。搜索结束之后，即可得到总的方案数。

具体实现方面，可以对传信息的关系进行预处理，使用列表存储有向边的关系，即可在 O(1) 的时间内得到特定节点的相邻节点（即可以沿着有向边一步到达的节点）。

class Solution {
    // 定义全局变量
    List<List<Integer>> edges;  // 存储有向边的关系
    int n, k, way;
    public int numWays(int n, int[][] relation, int k) {
        this.n = n;
        this.k = k;
        edges = new ArrayList<List<Integer>>();
        // 初始化边
        for(int i = 0; i < n; i++) {
            edges.add(new ArrayList<Integer>());
        }
        // 添加边
        for (int[] edge: relation) {
            int src = edge[0];
            int dst = edge[1];
            edges.get(src).add(dst);
        }
        dfs(0, 0);
        return way;
    }
    public void dfs(int src, int steps) {
        if (steps == k) {
            if (src == n-1)
                way++;
            return;
        }
        for (int nextIndex: edges.get(src)) {
            dfs(nextIndex, steps+1);
        }
    }
}

复杂度分析

• 时间复杂度：O(n^k)。最多需要遍历 k 层，每层遍历最多有 O(n) 个分支。
• 空间复杂度： O(n+m+k)。其中m为relation数组长度。空间复杂度主要取决于图的大小和递归调用栈的深度，保存有向图信息所需空间为O(n+m)，递归调用栈的深度不会超过 k。

BFS

也可以使用广度优先搜索计算方案数。从节点 0 出发做广度优先搜索，当遍历到 k 层时，如果位于节点 n−1，则将方案数加 1。搜索结束之后，即可得到总的方案数。

class Solution {
    public int numWays(int n, int[][] relation, int k) {
        List<List<Integer>> edges = new ArrayList<List<Integer>>();
        for (int i = 0; i < n; i++) {
            edges.add(new ArrayList<Integer>());
        }
        for (int[] edge : relation) {
            int src = edge[0], dst = edge[1];
            edges.get(src).add(dst);
        }

        int steps = 0;
        Queue<Integer> queue = new LinkedList<Integer>();
        queue.offer(0);
        while (!queue.isEmpty() && steps < k) {
            steps++;
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                int index = queue.poll();
                List<Integer> list = edges.get(index);
                for (int nextIndex : list) {
                    queue.offer(nextIndex);
                }
            }
        }

        int ways = 0;
        // 判断是否步数为k
        if (steps == k) {
            while (!queue.isEmpty()) {
                if (queue.poll() == n - 1) {
                    ways++;
                }
            }
        }
        return ways;
    }
}

复杂度分析

• 时间复杂度：O(n^k)。最多需要遍历 k 层，每层遍历最多有 O(n) 个分支。
• 空间复杂度：O(n+m+n^k)。其中m为relation数组的长度。空间复杂度主要取决于图的大小和队列的大小，保存有向图信息所需空间为O(n+m)，由于每层遍历最多有O(n)个分支，因此遍历k层时，队列大小O(n ^ k)。

DP

前两种方法都是通过在图中搜索计算方案数。可以换一个思路，这道题是计数问题，可以使用动态规划的方法解决。

定义动态规划的状态 dp[i][j]为经过i轮传递到编号j的玩家的方案数。

由于编号从0开始，当i=0时，一定位于编号0的玩家，不会传递到其他玩家，因此动态规划边界情况下：

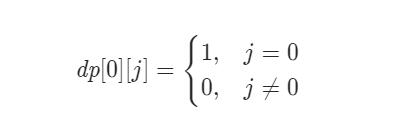
对于传信息的关系 [src, dist]，如果第i轮传递编号src的玩家，则第i+1轮可以从 src 传递到 dst 的玩家。因此在计算 dp[i+1][dst]，需要考虑可以传递到编号dst的所有玩家。

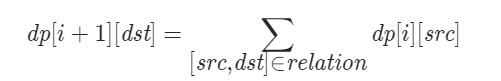
最终得到 dp[k][n−1] 即为总的方案数。

class Solution {
    public int numWays(int n, int[][] relation, int k) {
        int[][] dp = new int[k + 1][n];
        dp[0][0] = 1;
        for (int i = 0; i < k; i++) {
            for (int[] edge : relation) {
                int src = edge[0], dst = edge[1];
                dp[i + 1][dst] += dp[i][src];
            }
        }
        return dp[k][n - 1];
    }
}

dp[i][]的值只与dp[i-1][]有关，因此可以把二维数组变为一维数组.

class Solution {
    public int numWays(int n, int[][] relation, int k) {
        int[] dp = new int[n];
        dp[0] = 1;
        for (int i = 0; i < k; i++) {
            int[] next = new int[n];
            for (int[] edge : relation) {
                int src = edge[0], dst = edge[1];
                next[dst] += dp[src];
            }
            dp = next;
        }
        return dp[n - 1];
    }
}

复杂度分析

• 时间复杂度：O(km)。其中 m 为relation 数组的长度。
• 空间复杂度：O(n)。

BUG代码：

class Solution {
    public int numWays(int n, int[][] relation, int k) {
        int[][] dp = new int[2][n];
        dp[0][0] = 1;
        for (int i = 0; i < k; i++) {
            for (int[] edge: relation) {
                int src = edge[0];
                int dst = edge[1];
                dp[((i+1)&1)][dst] += dp[(i&1)][src];                
            }
        }
        return dp[1][n-1];
    }
}