二叉树的定义常见的性质及其存储结构（C语言）

Posted 2021-08-04 bfhonor

一、二叉树的定义与基本术语

（一）基本概念

• 二叉树是n（n≥0）个结点的有限集合：
  ① 或者为空二叉树，即n = 0。
  ② 或者由一个根结点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树又分别是一棵二叉树。
• 特点：①每个结点至多只有两棵子树 ②左右子树不能颠倒（二叉树是有序树）【注意区别：度为2的有序树】
  

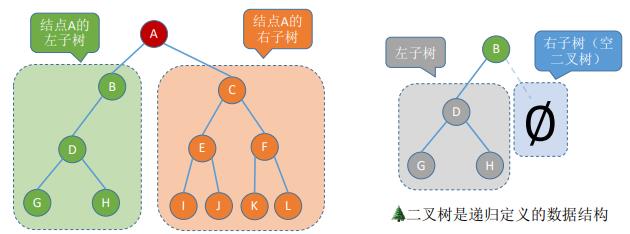
1. 二叉树的五种状态

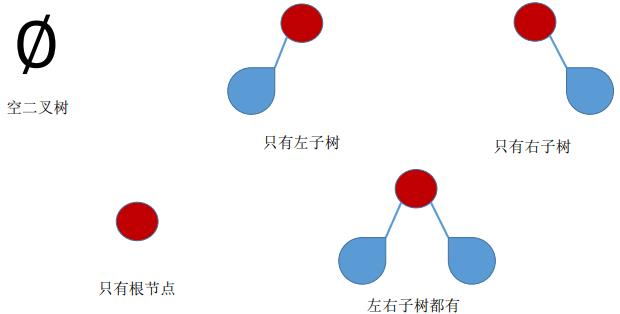
（二）几种特殊的二叉树

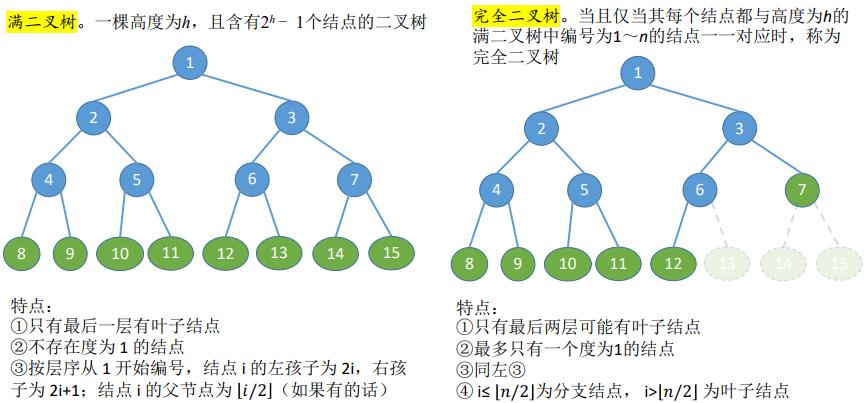
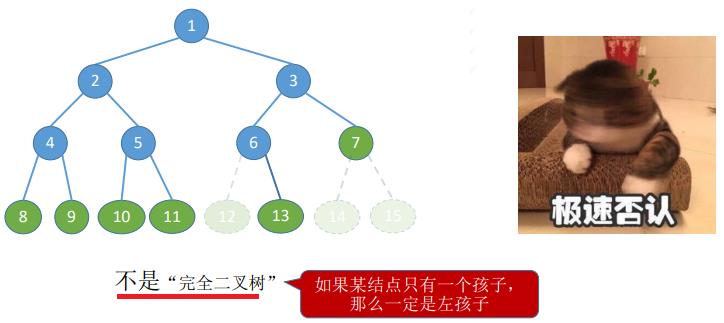
1. 满二叉树 && 完全二叉树

2. 二叉排序树

• 一棵二叉树或者是空二叉树，或者是具有如下性质的二叉树：
  ①、左子树上所有结点的关键字均小于根结点的关键字；
  ②、右子树上所有结点的关键字均大于根结点的关键字。
• 左子树和右子树又各是一棵二叉排序树。
• 二叉排序树可用于元素的排序、搜索
  

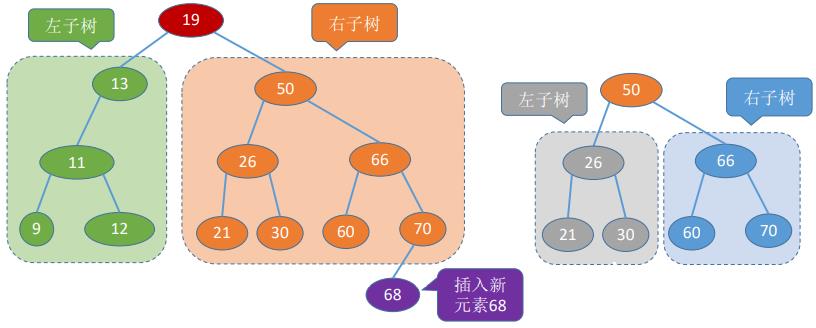
3. 平衡二叉树

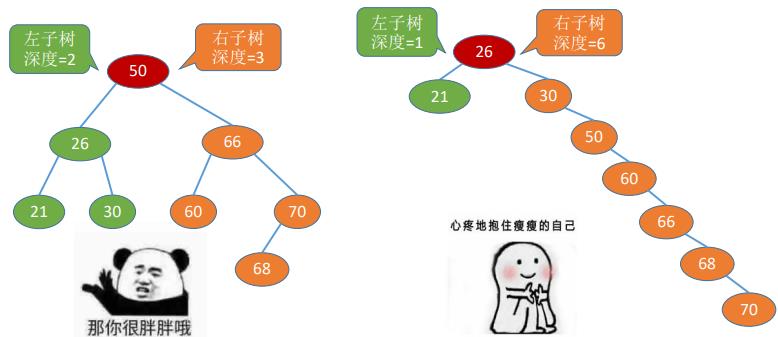
• 平衡二叉树。树上任一结点的左子树和右子树的深度之差不超过1。
• 平衡二叉树能有更高的搜索效率
  

二、二叉树常考性质

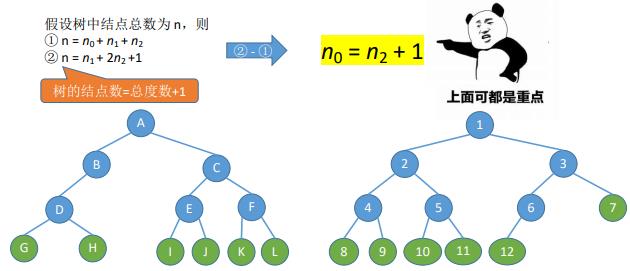
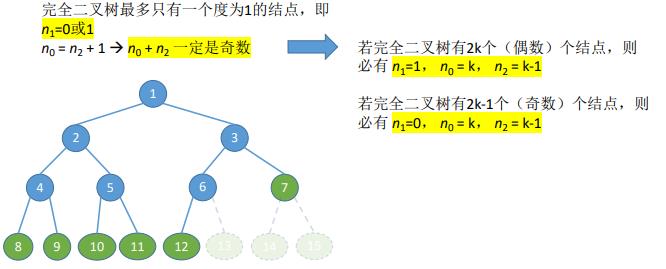
1. 常见考点1：设非空二叉树中度为0、1和2的结点个数分别为n0、n1和n2，则 n0 = n2 + 1（叶子结点比二分支结点多一个）

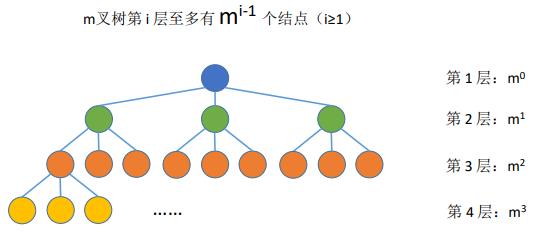
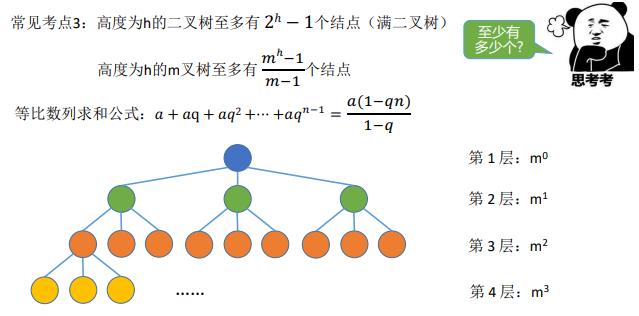
2. 常见考点2：二叉树第 i 层至多有 2ⁱ-1 个结点（i≥1）

3. 常见考点3：高度为h的二叉树至多有 2ℎ − 1个结点（满二叉树）

三、完全二叉树的常考性质

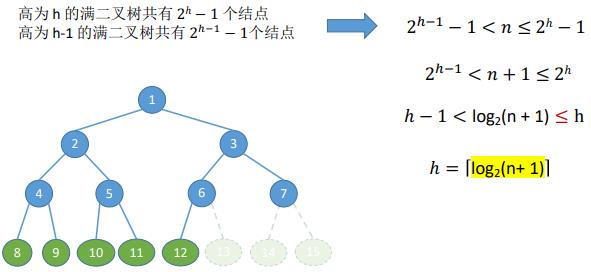
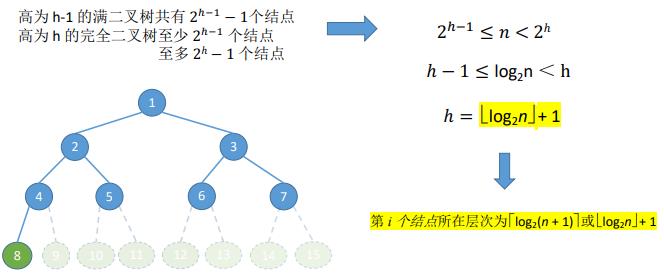
1. 常见考点1：具有n个（n > 0）结点的完全二叉树的高度h为⌈log₂(n + 1)⌉或 ⌊log₂n⌋ + 1

2. 常见考点2：对于完全二叉树，可以由的结点数 n 推出度为0、1和2的结点个数为n0、n1和n2

四、二叉树的存储结构

（一）二叉树的顺序存储

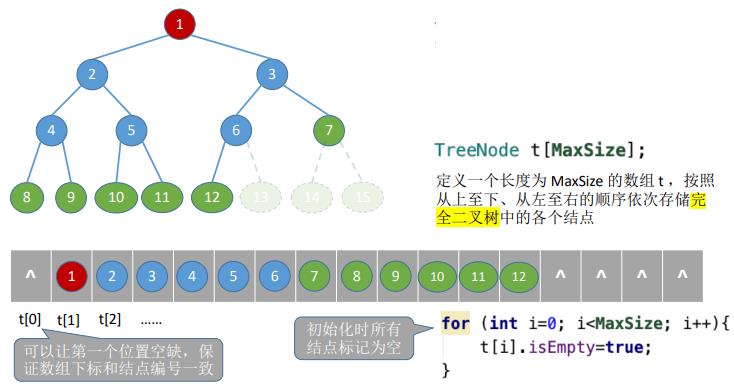
#define MaxSize 100
struct TreeNode{
	ElemType value;//结点中的数据元素
	bool isEmpty;//结点是否为空
};

TreeNode t[MaxSize];//定义一个长度为MaxSize的数组t,按照从上至下、从左至右的顺序依次存储完全二叉树中的各个结点

//初始化时所有结点标记为空
for(int i=0; i<MaxSize; i++){
	t[i].isEmpty = ture;
}

• 几个重要常考的基本操作：
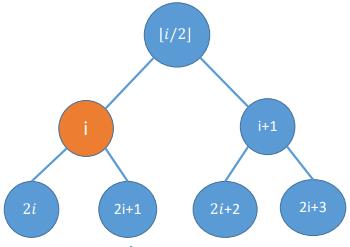
  ①、i 的左孩子——2i
  ②、i 的右孩子——2i+1
  ③、i 的父节点—— ⌊i/2⌋
  ④、i 所在的层次—— ⌈log₂(n + 1)⌉或 ⌊log₂n⌋ + 1
• 若完全二叉树中共有n个结点，则
  ①、判断 i 是否有左孩子？——2i ≤ n ?
  ②、判断 i 是否有右孩子？——2i+1 ≤ n ?
  ③、判断 i 是否是叶子/分支结点？——i > ⌊i/2⌋?

倘若不是完全二叉树，依然采取顺序存储会发生什么呢？

• 最大的问题就是：我们无法从结点编号反映出结点间的逻辑关系。
  
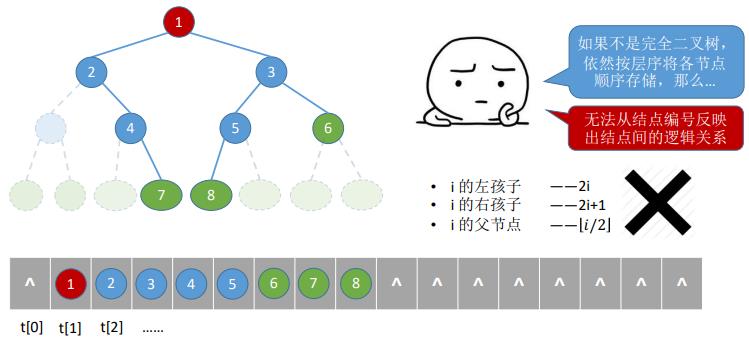
• 二叉树的顺序存储中，我们要是把二叉树的结点编号与完全二叉树对应起来的话，我们就可以很好的判断左右子节点。
  
  
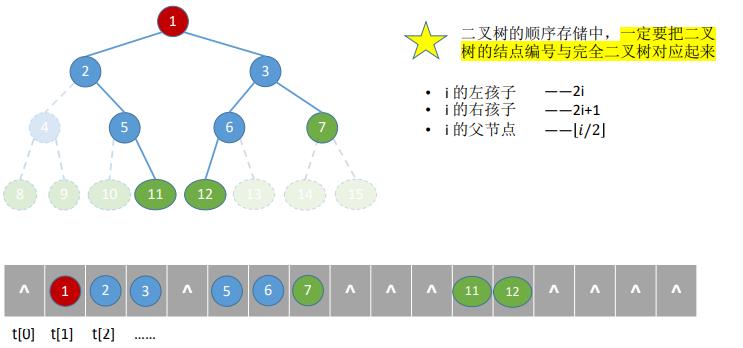
• 但是，会出现一个问题，那就是如果这是一个非完全二叉树呢？那么我们就不能通过下面的方法来判断结点i是否有左右子节点等问题了
• 若完全二叉树中共有n个结点，则
  ①、判断 i 是否有左孩子？——2i ≤ n 【X】| 2i.isEmpty==true【√】
  ②、判断 i 是否有右孩子？——2i+1 ≤ n 【X】| (2i+1).isEmpty==true【√】
  ③、判断 i 是否是叶子/分支结点？——i > ⌊i/2⌋ 【X】
• 最坏情况：高度为 h 且只有 h 个结点的单支树（所有结点只有右孩子），也至少需要 2^h-1 个存储单元
• 结论：二叉树的顺序存储结构，只适合存储完全二叉树

（二）二叉树的链式存储

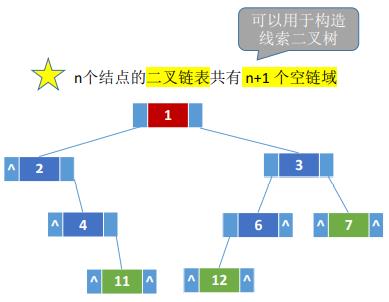
• ⭐⭐⭐⭐⭐n个结点的二叉链表共有 n+1 个空链域

//二叉树的结点（链式存储）
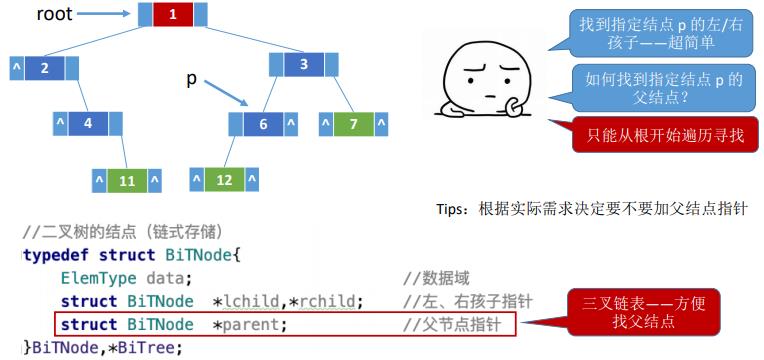
typedef struct BiTNode{
	ElemType data;	//数据域
	struct BiTNode *lchild,*rchild;	//左、右孩子指针
}BiTNode,*BiTree;

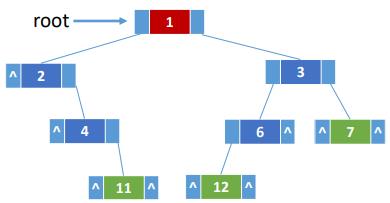
struct ElemType{
	int value;
};

typedef struct BiTNode{
	ElemType data;
	struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

//定义一个空树
BiTree root = NULL;

//插入根节点
root = (BiTree) malloc(sizeof(BiTNode));
root -> data = {1};
root -> lchild = NULL;
root -> rchild = NULL;

//插入新的结点
BiTNode * p = (BiTNode *)malloc(sizeof(BiTNode));
p -> data = {2};
p -> lchild = NULL;
p -> rchild = NULL;
root -> lchild = p;	//作为根节点的左孩子