Acwing 1081. 度的数量（以及本人对数位dp的浅薄理解）

Posted 2021-08-04 Jozky86

题意：

求给定区间 [X,Y] 中满足下列条件的整数个数：这个数恰好等于 K 个互不相等的 B 的整数次幂之和。

题解：

数位DP
技巧1：[X,Y]=>f(Y)-f(X-1)
技巧2：用树的方式来考虑。

在本题中，题意是问[X,Y]中的数 转发成B进制，B进制有K位是1
比如样例中：17 ，k=2，B=2
就是把17转成二进制，看二进制中是否有K个1
17的二进制是：10001，说明17=2⁴+2⁰,符合要求
我们现在想具体做法:我们利用前缀和的方式，想法1~n之间符合要求的个数，这样就可以方便求出任意区间的数量。
对于一个N位数，我们将N的各位拆成an-1到a0（从高到底），然后我们用树的形式来考虑，对于最高位an-1，他可以是a_n-1或者是0到a_n-1-1之间的数，如果是0到a_n-1-1之间的数，我们具体讨论，如果是1，说明剩下位置是需要k-1个1，如果是非1，剩下位置只需要k个1，直接用组合数就可以表示（如图），而对于第an-1位是a_n-1的话我们可以继续分解

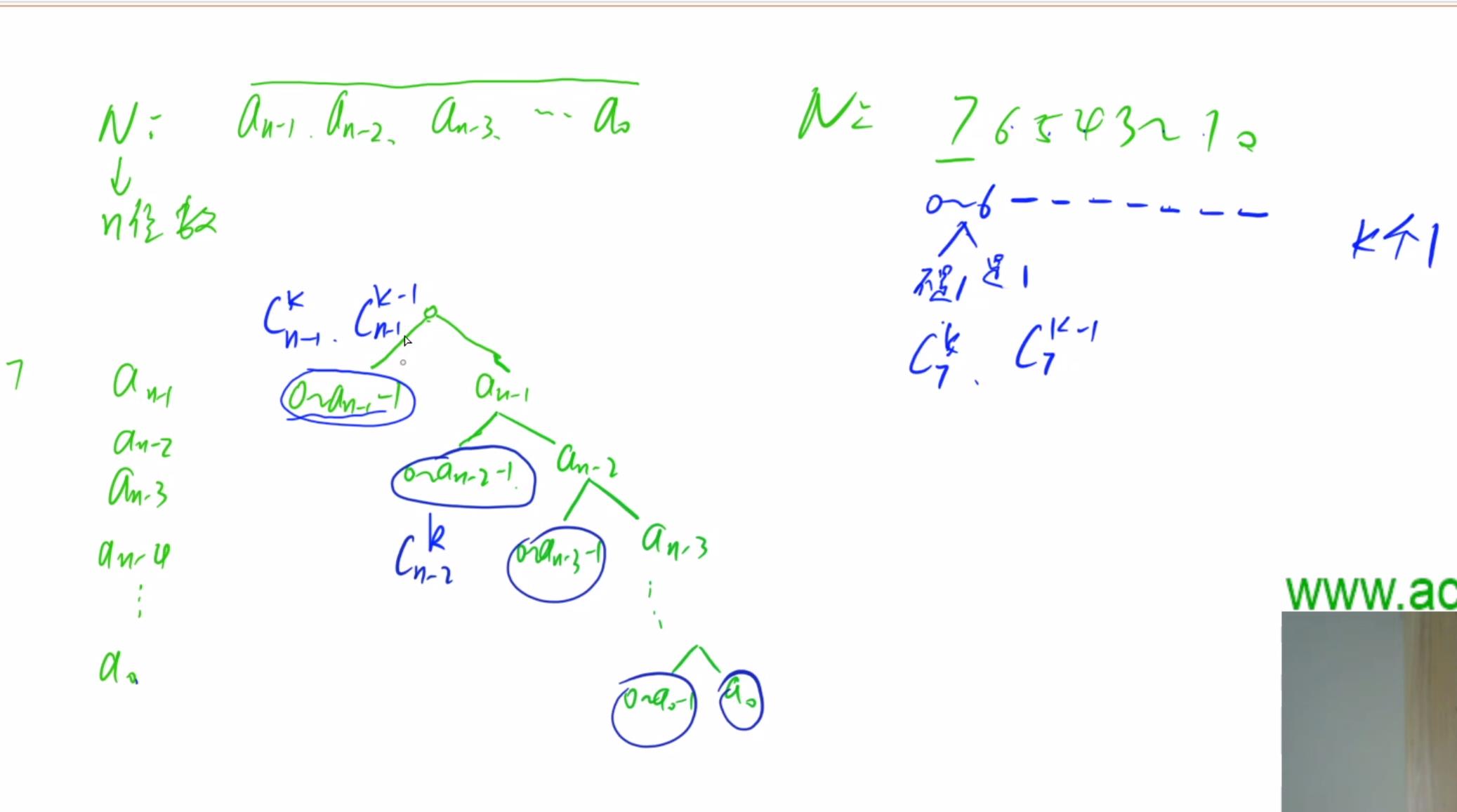
参考题解（下图来源）

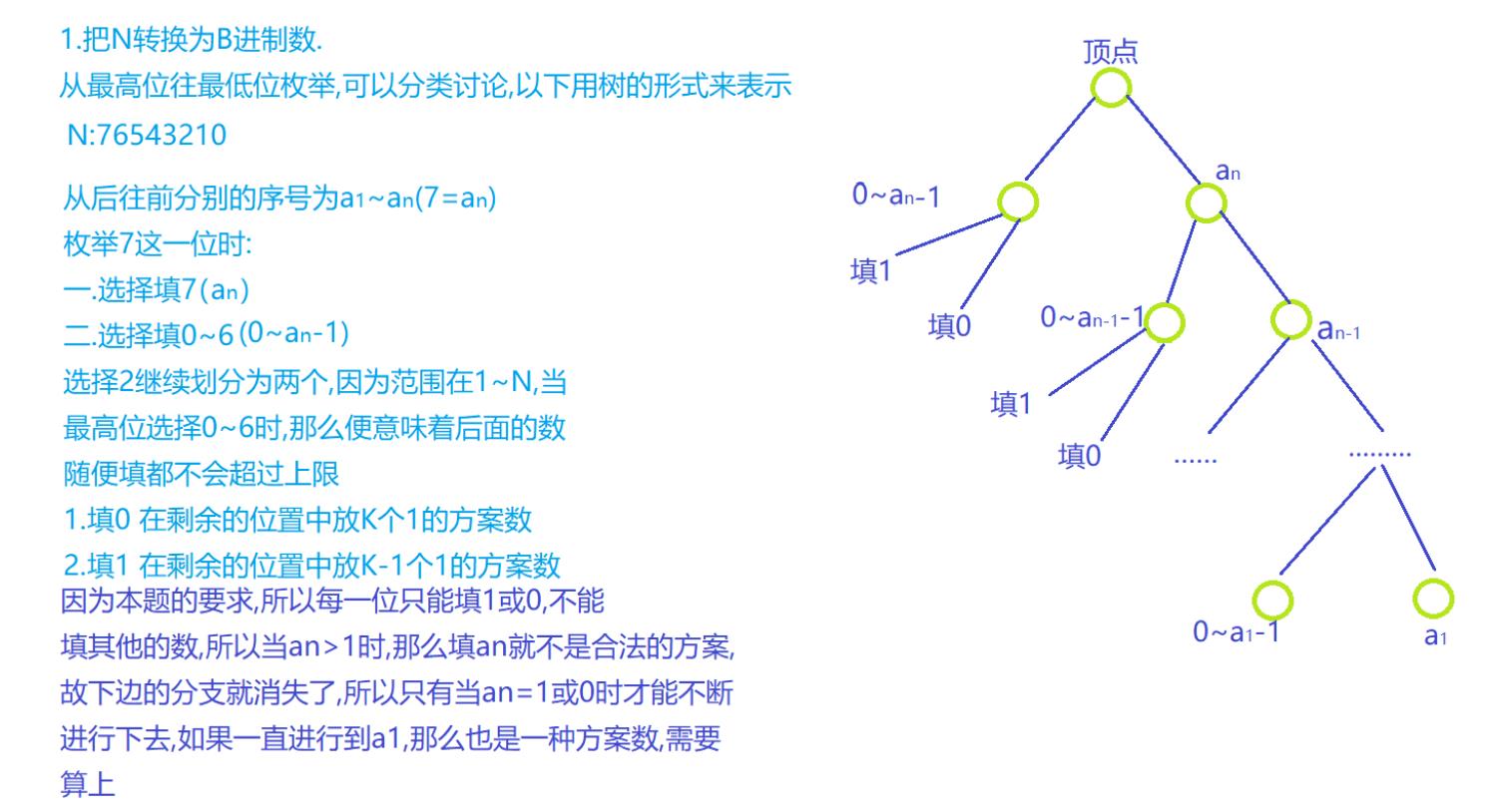
谈谈我对数位dp的理解，为什么要拆分成左右两侧，左侧是0 ~ a_n-1，右侧为a_n,我的理解：数位dp就是一种优化的统计的方式，因为我们计算的是1~n中所有满足答案的情况，那统计的x一定要小于等于n，我们将n拆成各位，我们从高位向低位枚举时，假如说n是7854，我们将n拆成开，就是4位，从高到低分别是7，8，5，4，我们在枚举第一位（最高位时），最高位如果我们枚举0 ~ 6，那么后三位可以是任意数，因为肯定比7854小，对不对，然后统计这部分答案。如果我们枚举是7，那你后三位不能随便枚举，如果你第二位枚举9，那就超出范围了，为了避免超出范围，如果我们第一位枚举7，那我们就看第二位，第二位的上限是8，那我们就枚举 0 ~ 7 ，这样后两位就可以随便枚举，统计答案，然后我们第二位取上限8，再往后推一位。。。依次类推，终点就是我们推到7854，就是n本身（我们在推的过程中是加了判断条件，如果不满足条件就break，如果能推到最后，说明最终这个n也是满足条件的）。这样说不知道能不能理解

代码：

#include<bits/stdc++.h>
using namespace std;
const int N = 35; //位数

int f[N][N];// f[a][b]表示从a个数中选b个数的方案数，即组合数

int K, B; //K是能用的1的个数，B是B进制

//求组合数：预处理
void init(){
    for(int i=0; i< N ;i ++)
        for(int j =0; j<= i ;j++)
            if(!j) f[i][j] =1;
            else f[i][j] =f[i-1][j] +f[i-1][j-1];
}



 //求区间[0,n]中的 “满足条件的数” 的个数
 //“满足条件的数”是指：一个数的B进制表示，其中有K位是1、其他位全是0
int dp(int n){

    if(n == 0) return 0; //如果上界n是0，直接就是0种

    vector<int> nums; //存放n在B进制下的每一位
    //把n在B进制下的每一位单独拿出来
    while(n) nums.push_back( n% B) , n/= B;

    int res = 0;//答案：[0,n]中共有多少个合法的数

    //last在数位dp中存的是：右边分支往下走的时候保存前面的信息 
    //遍历当前位的时候，记录之前那些位已经占用多少个1，那么当前还能用的1的个数就是K-last
    int last = 0; 

    //从最高位开始遍历每一位
    for(int i = nums.size()-1; i>= 0; i--){

        int x = nums[i]; //取当前位上的数

        if(x>0)
		{ //只有x>0的时候才可以讨论左右分支


            //当前位填0，从剩下的所有位（共有i位）中选K-last个数。
            //对应于：左分支中0的情况，合法
            res += f[i][ K -last];//i个数中选K-last个数的组合数是多少，选出来这些位填1，其他位填0


            if(x > 1)
			{
                //当前位填1，从剩下的所有位（共有i位）中选K-last-1个数。
                //对应于：左分支中填1的情况，合法
               if(K - last -1 >= 0) res += f[i][K -last -1];//i个数中选K-last-1个数填1的组合数是多少
               //对应于：左分支中其他情况（填大于1的数）和此时右分支的情况（右侧此时也>1），不合法！！！直接break。
                break;
            }

            //上面统计完了**左分支**的所有情况，和右分支大于1的情况，

            //这个else 是x==1，
            //对应于：右分支为1的情况，即限定值为1的情况，也就是左分支只能取0
            //此时的处理是，直接放到下一位来处理
            //只不过下一位可使用的1的个数会少1，体现在代码上是last+1

            else if(x==1)//相当于限定值为1 
			{
                last ++;
                //如果已经填的个数last > 需要填的个数K，不合法break
                if(last > K) break;
            }

        }
        //上面处理完了这棵树的**所有**左分支，就剩下最后一种右分支的情况
        // 也就是遍历到最后1位，在vector中就是下标为0的地方：i==0；
        // 并且最后1位取0，才算作一种情况res++。因为最后1位不为0的话，已经被上面的ifelse处理了。
        if(i==0 && last == K) res++; 
    }

    return res;
}

int main(){
    init();
    int l,r;
    cin >>  l >> r >> K >>B;
    cout<< dp(r) - dp(l-1) <<endl;  
}