笛卡尔树

Posted 2021-06-28 onlyblues

笛卡尔树

笛卡尔树是一种特殊的二叉树，其结点包含两个关键字K1和K2。首先笛卡尔树是关于K1的二叉搜索树，即结点左子树的所有K1值都比该结点的K1值小，右子树则大。其次所有结点的K2关键字满足优先队列（不妨设为最小堆）的顺序要求，即该结点的K2值比其子树中所有结点的K2值小。给定一棵二叉树，请判断该树是否笛卡尔树。

输入格式:

输入首先给出正整数N（≤1000），为树中结点的个数。随后N行，每行给出一个结点的信息，包括：结点的K1值、K2值、左孩子结点编号、右孩子结点编号。设结点从0~(N-1)顺序编号。若某结点不存在孩子结点，则该位置给出−1。

输出格式:

输出 YES 如果该树是一棵笛卡尔树；否则输出 NO 。

输入样例1:

6
8 27 5 1
9 40 -1 -1
10 20 0 3
12 21 -1 4
15 22 -1 -1
5 35 -1 -1

输出样例1:

YES

输入样例2:

6
8 27 5 1
9 40 -1 -1
10 20 0 3
12 11 -1 4
15 22 -1 -1
50 35 -1 -1

输出样例2:

NO

 

解题思路

　　这道题没什么难度，判断是否是搜索树和最小堆写个递归来实现就好了。

　　记录的原因是因为我又忽略了判断搜索树的条件了...我又犯的错误是只用根节点的值来与左子树的根节点的值和右子树根节点的值比较，如果根节点比左子树的根节点小，比右子树的根节点大，就说明这颗书是BST。实际上这种判断方法是很有问题的，比如下图：

　　如果按照上面的方法来判断，无论是先序、中序还是后序，都会判定为BST，但实际上它并不是BST。

　　正确的判断方法是，根节点的值比左子树所有节点的值大，比右子树所有节点的值小，因此还需要再写个递归代码来做这件事情。

　　AC代码如下：

 1 #include <cstdio>
 2 using namespace std;
 3 
 4 const int MAXN = 1001;
 5 
 6 struct TNode {
 7     int k1, k2;
 8     int left, right;
 9 }tree[MAXN];
10 
11 bool judge(int k1, int root, bool flag) {
12     if (root == -1) return true;
13     if (flag) {
14         if (k1 > tree[root].k1) return judge(k1, tree[root].left, flag) && judge(k1, tree[root].right, flag);
15         else return false;
16     }
17     else {
18         if (k1 < tree[root].k1) return judge(k1, tree[root].left, flag) && judge(k1, tree[root].right, flag);
19         else return false;
20     }
21 }
22 
23 bool isBST(int root) {
24     if (root == -1) return true;
25     if (judge(tree[root].k1, tree[root].left, true) && judge(tree[root].k1, tree[root].right, false)) return isBST(tree[root].left) && isBST(tree[root].right);
26     else return false;
27 }
28 
29 bool isMinHeap(int root) {
30     if (root == -1) return true;
31     if (isMinHeap(tree[root].left) && isMinHeap(tree[root].right)) {
32         if (tree[root].left != -1 && tree[root].k2 > tree[tree[root].left].k2) return false; 
33         if (tree[root].right != -1 && tree[root].k2 > tree[tree[root].right].k2) return false;
34         else return true;
35     }
36     else return false;
37 }
38 
39 int main() {
40     int n;
41     scanf("%d", &n);
42     bool notRoot[n] = {false};
43     for (int i = 0; i < n; i++) {
44         int k1, k2, left, right;
45         scanf("%d %d %d %d", &k1, &k2, &left, &right);
46         tree[i] = {k1, k2, left, right};
47         if (left != -1) notRoot[left] = true;
48         if (right != -1) notRoot[right] = true;
49     }
50     
51     int root = 0;
52     while (notRoot[root]) {
53         root++;
54     }
55     printf("%s", isBST(root) && isMinHeap(root) ? "YES" : "NO");
56     
57     return 0;
58 }

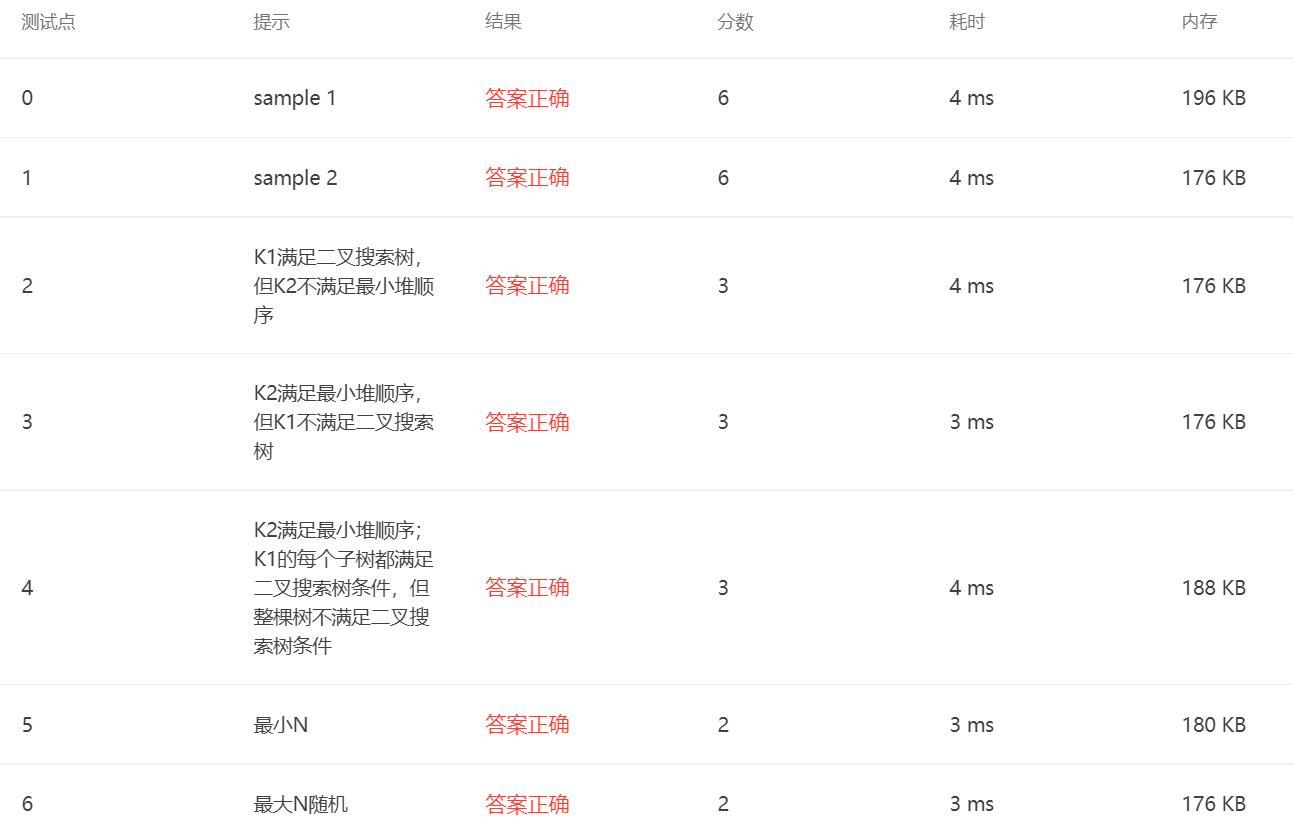
　　还有一种判断是否是BST的方法，就是利用BST的特性，根据关键字K1进行中序遍历，将得到的序列进行比较，如果这个序列是递增的，就说明这颗树是BST，如果发现某个值比它后一个值大，就说明不是BST。

　　一开始没有想到这种方法，真的是太妙了。

　　AC代码如下：

 1 #include <cstdio>
 2 #include <vector>
 3 using namespace std;
 4 
 5 const int MAXN = 1001;
 6 vector<int> in;
 7 
 8 struct TNode {
 9     int k1, k2;
10     int left, right;
11 }tree[MAXN];
12 
13 void inOrderTraversal(int root) {
14     if (root != -1) {
15         inOrderTraversal(tree[root].left);
16         in.push_back(tree[root].k1);
17         inOrderTraversal(tree[root].right); 
18     }
19 }
20 
21 bool isBST(int root) {
22     inOrderTraversal(root);
23     for (int i = 0; i < in.size() - 1; i++) {
24         if (in[i] > in[i + 1]) return false;
25     }
26     return true;
27 }
28 
29 bool isMinHeap(int root) {
30     if (root == -1) return true;
31     if (isMinHeap(tree[root].left) && isMinHeap(tree[root].right)) {
32         if (tree[root].left != -1 && tree[root].k2 > tree[tree[root].left].k2) return false; 
33         if (tree[root].right != -1 && tree[root].k2 > tree[tree[root].right].k2) return false;
34         else return true;
35     }
36     else return false;
37 }
38 
39 int main() {
40     int n;
41     scanf("%d", &n);
42     bool notRoot[n] = {false};
43     for (int i = 0; i < n; i++) {
44         int k1, k2, left, right;
45         scanf("%d %d %d %d", &k1, &k2, &left, &right);
46         tree[i] = {k1, k2, left, right};
47         if (left != -1) notRoot[left] = true;
48         if (right != -1) notRoot[right] = true;
49     }
50     
51     int root = 0;
52     while (notRoot[root]) {
53         root++;
54     }
55     printf("%s", isBST(root) && isMinHeap(root) ? "YES" : "NO");
56     
57     return 0;
58 }

 

参考资料

　　数据结构与算法题目集7-31——笛卡尔树：https://blog.csdn.net/qq_41231926/article/details/84888050