数组-数组的常见算法
Posted 犄角旮旯是程序媛吖
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数组-数组的常见算法相关的知识,希望对你有一定的参考价值。
一、数组的创建与元素赋值
- 杨辉三角(针对二维数组)
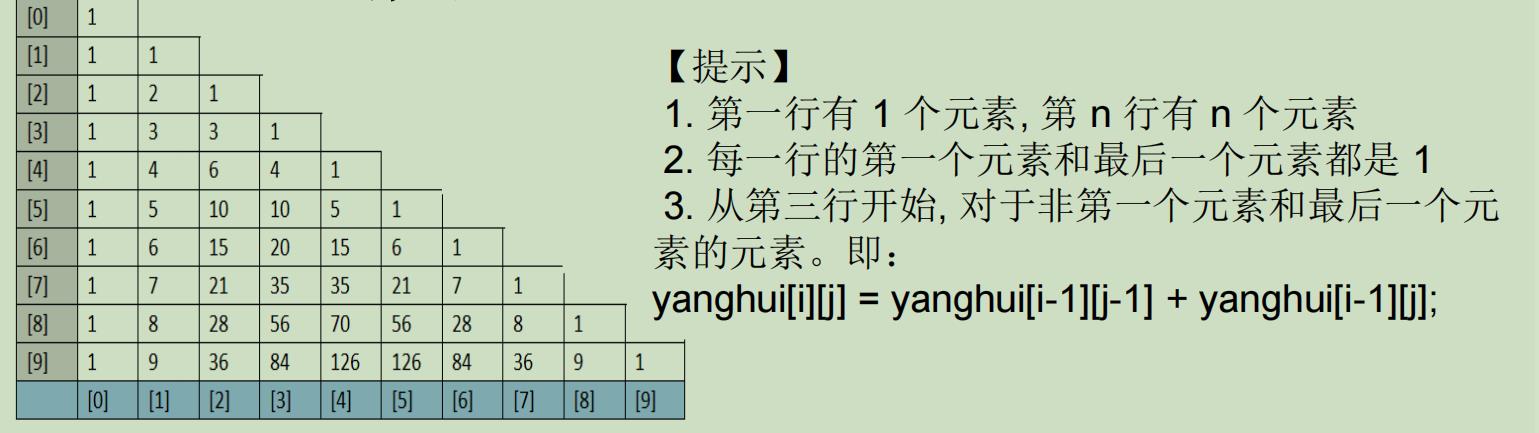
/*
使用二维数组打印一个10行杨辉三角
【提示】
1.第一行有1个元素,第n行有n个元素
2.每一行的第一个元素和最后一个元素都是1
3.从第三行开始,对于非第一个元素和最后一个元素的元素
即:yanghui[i][j] = yanghui[i-1][j-1] + yanghui[i-1][j];
*/
//声明并初始化二维数组
int[][] triAngel = new int[10][];
//给数组的元素赋值
for(int i = 0;i < triAngel.length;i++){
//第一行有1个元素,第n行有n个元素
triAngel[i] = new int[i + 1];
//给首末元素赋值:每一行的第一个元素和最后一个元素都是1
triAngel[i][0] = 1;
triAngel[i][i] = 1;
//给每行的非首末元素赋值
if(i > 1){//此处if可去掉
for(int j = 1;j < triAngel[i].length - 1;j++){
triAngel[i][j] = triAngel[i-1][j-1] + triAngel[i-1][j];
}
}
}
//遍历二维数组
for(int i = 0;i < triAngel.length;i++){
for(int j = 0; j < triAngel[i].length;j++){
System.out.print(triAngel[i][j] + " ");
}
System.out.println();
}
- 回形数(针对二维数组)

class RectangleTest {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("输入一个数字");
int len = scanner.nextInt();
int[][] arr = new int[len][len];
int s = len * len;
/*
* k = 1:向右 k = 2:向下 k = 3:向左 k = 4:向上
*/
int k = 1;
int i = 0, j = 0;
for (int m = 1; m <= s; m++) {
if (k == 1) {
if (j < len && arr[i][j] == 0) {
arr[i][j++] = m;
} else {
k = 2;
i++;
j--;
m--;
}
} else if (k == 2) {
if (i < len && arr[i][j] == 0) {
arr[i++][j] = m;
} else {
k = 3;
i--;
j--;
m--;
}
} else if (k == 3) {
if (j >= 0 && arr[i][j] == 0) {
arr[i][j--] = m;
} else {
k = 4;
i--;
j++;
m--;
}
} else if (k == 4) {
if (i >= 0 && arr[i][j] == 0) {
arr[i--][j] = m;
} else {
k = 1;
i++;
j++;
m--;
}
}
}
// 遍历
for (int m = 0; m < arr.length; m++) {
for (int n = 0; n < arr[m].length; n++) {
System.out.print(arr[m][n] + "\\t");
}
System.out.println();
}
}
}
方式二:
class RectangleTest1 {
public static void main(String[] args) {
int n = 7;
int[][] arr = new int[n][n];
int count = 0; // 要显示的数据
int maxX = n - 1; // x轴的最大下标
int maxY = n - 1; // Y轴的最大下标
int minX = 0; // x轴的最小下标
int minY = 0; // Y轴的最小下标
while (minX <= maxX) {
for (int x = minX; x <= maxX; x++) {
arr[minY][x] = ++count;
}
minY++;
for (int y = minY; y <= maxY; y++) {
arr[y][maxX] = ++count;
}
maxX--;
for (int x = maxX; x >= minX; x--) {
arr[maxY][x] = ++count;
}
maxY--;
for (int y = maxY; y >= minY; y--) {
arr[y][minX] = ++count;
}
minX++;
}
for (int i = 0; i < arr.length; i++) {
for (int j = 0; j < arr.length; j++) {
String space = (arr[i][j] + "").length() == 1 ? "0" : "";
System.out.print(space + arr[i][j] + " ");
}
System.out.println();
}
}
}
- 6个数,1-30之间随机生成且不重复
//创建一个长度为6的int型数组,取值范围为1~30,同时元素值各不相同
//方式一:
int[] arr = new int[6];
for(int i = 0;i < arr.length;i++){
arr[i] = (int) (Math.random() * 30) + 1;
boolean flag = false;
while(true){
for(int j = 0;j < i;j++){
if(arr[i] == arr[j]){
flag = true;
break;
}
}
if (flag){
arr[i] = (int)(Math.random() * 30) + 1;
flag = false;
continue;
}
break;
}
}
for(int i = 0;i < arr.length;i++){
System.out.println(arr[i]);
}
//方式二:
int[] arr = new int[6];
for(int i = 0;i < arr.length;i++){
arr[i] = (int)(Math.random() * 30) + 1;
for(int j = 0;j < i;j++){
if(arr[i] == arr[j]){
i--;
break;
}
}
}
for(int i = 0;i < arr.length;i++){
System.out.println(arr[i]);
}
二、针对于数值型的数组
最大值、最小值、总和、平均数等
//算法的考查:求数值型数组中元素的max、min、sum、Average
//定义一个int型的一维数组,包含10个元素,分别赋一些随机整数,然后求出所有元素的max、min、sum、Average并输出
//要求:所有随机数都是两位数
int[] arr = new int[10];
int max = arr[0];
int min = 99;
int sum = 0;
double Average = 0.0;
for(int i = 0;i < arr.length;i++){
arr[i] = (int)(Math.random() * 100) + 1;
System.out.print(arr[i] + " ");
//求max
if(arr[i] > max){
max = arr[i];
}
//求min
if(arr[i] < min){
min = arr[i];
}
//求sum
sum = sum + arr[i];
//求Average
Average = sum / arr.length;
}
System.out.println();
System.out.println("max = " + max);
System.out.println("min = " + min);
System.out.println("sum = " + sum);
System.out.println("Average = " + Average);
三、数组的赋值与复制
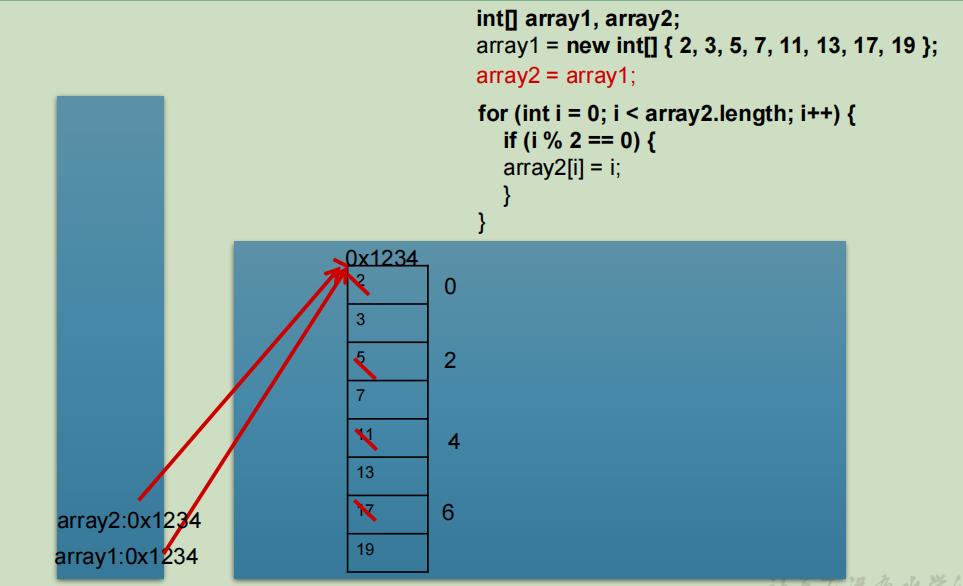
int[] array1,array2;
array1 = new int[]{1,2,3,4};
1.赋值
array2 = array1;
- 如何理解:将array1保存的数组的地址值赋给了array2,使得array1和array2共同指向堆空间中的同一个数组实体
2.复制
array2 = new int[array1.length];
for(int i = 0;i < array2.length;i++){
array2[i] = array1[i];
}
- 如何理解:通过new的方式,给array2在堆空间中新开辟了数组的空间,将array1数组中的元素值一个一个的赋值到array2数组中

四、数组元素的反转
//反转方式一:
for(int i = 0;i < str1.length / 2;i++){
String temp = str1[i];
str1[i] = str1[str1.length - i - 1];
str1[str1.length - i - 1] = temp;
}
//反转方式二:
for(int i=0,j = str1.length - 1;i < j;i++,j--){
String temp = str1[i];
str1[i] = str1[j];
str1[j] = temp;
}
for (int i = 0;i < str1.length;i++){
System.out.print(str1[i] + "\\t");
}
五、数组中指定元素的查找(搜索/检索)
1.线性查找(地毯式搜索)
- 实现思路:通过遍历的方式,一个一个的数据进行比较、查找
//线性查找方式一:
String target = "BB";
boolean isFlag = true;
for(int i = 0;i < str1.length;i++){
//equals比较的是内容
if(target.equals(str1[i])){
System.out.println("找到了指定元素,位置在索引为" + i + "的地方");
isFlag = false;
break;
}
}
if(isFlag){
System.out.println("不好意思,未查找到此元素");
}
//线性查找方式二:
String dest = "BB";
for(int i = 0;i < str1.length;i++){
//equals比较的是内容
if(dest.equals(str1[i])){
System.out.println("找到了指定元素,位置在索引为" + i + "的地方");
break;
}
//循环条件不满足了,就跳出循环
if(i == str1.length){
System.out.println("不好意思,未查找到此元素");
}
}
- 适用性:具有普遍适用性(类型上无严格要求,数组本身也没有太多要求)
2.二分法查找
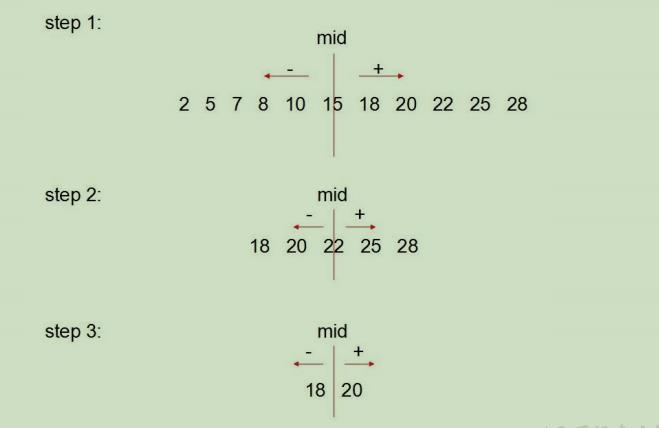
- 实现思路:每次比较中间值,折半的方式检索
//二分法查找(折半查找),所要查找的数组必须有序(熟悉)
int[] arr = new int[]{2,5,7,8,10,15,18,20,22,25,28};
int element = -6;
//初始化首索引
int start = 0;
//初始化末索引
int end = arr.length - 1;
boolean flag = true;
while(start <= end){
//中间位置索引
int mid = (start + end)/2;
//如果需要查找的元素正好是中间索引位置的元素
if(element == arr[mid]){
System.out.print("找到了指定元素,位置在索引为" + mid + "的地方");
flag = false;
break;
}else if(arr[mid] > element){
end = mid - 1;
}else{
start = mid + 1;
}
}
if(flag){
System.out.println("不好意思,未查找到此元素");
}
- 适用性:前提是数组必须要有序
六、数组的排序算法
十大内部排序算法
1.选择排序
- ·直接选择排序
public class SelectSort {
public static void selectSort(int[] data) {
//选择排序-直接选择排序
System.out.println("开始排序");
int arrayLength = data.length;
for (int i = 0; i < arrayLength - 1; i++) {
for (int j = i + 1; j < arrayLength; j++) {
if (data[i] - data[j] > 0) {
int temp = data[i];
data[i] = data[j];
data[j] = temp;
}
}
System.out.println(java.util.Arrays.toString(data));
}
}
public static void main(String[] args) {
int[] data = { 9, -16, 21, 23, -30, -49, 21, 30, 30 };
System.out.println("排序之前:\\n" + java.util.Arrays.toString(data));
selectSort(data);
System.out.println("排序之后:\\n" + java.util.Arrays.toString(data));
}
}
- ·堆排序
public class SelectSort_HeapSort {
public static void heapSort(int[] data) {
//选择排序-堆排序
System.out.println("开始排序");
int arrayLength = data.length;
// 循环建堆
for (int i = 0; i < arrayLength - 1; i++) {
// 建堆
buildMaxdHeap(data, arrayLength - 1 - i);
// 交换堆顶和最后一个元素
swap(data, 0, arrayLength - 1 - i);
System.out.println(java.util.Arrays.toString(data));
}
}
// 对data数组从0到lastIndex建大顶堆
private static void buildMaxdHeap(int[] data, int lastIndex) {
// 从lastIndex处节点(最后一个节点)的父节点开始
for (int i = (lastIndex - 1) / 2; i >= 0; i--) {
// k保存当前正在判断的节点
int k = i;
// 如果当前k节点的子节点存在
while (k * 2 + 1 <= lastIndex) {
// k节点的左子节点的索引
int biggerIndex = 2 * k + 1;
// 如果biggerIndex小于lastIndex,即biggerIndex +1
// 代表k节点的右子节点存在
if (biggerIndex < lastIndex) {
// 如果右子节点的值较大
if (data[biggerIndex] - data[biggerIndex + 1] < 0) {
// biggerIndex总是记录较大子节点的索引
biggerIndex++;
}
}
// 如果k节点的值小于其较大子节点的值
if (data[k] - data[biggerIndex] < 0) {
// 交换它们
swap(data, k, biggerIndex);
// 将biggerIndex赋给k,开始while循环的下一次循环
// 重新保证k节点的值大于其左、右节点的值
k = biggerIndex;
} else {
break;
}
}
}
}
// 交换data数组中i、j两个索引处的元素
private static void swap(int[] data, int i, int j) {
int temp = data[i];
data[i] = data[j];
data[j] = temp;
}
public static void main(String[] args) {
int[] data = { 9, -16, 21, 23, -30, -49, 21, 30, 30 };
System.out.println("排序之前:\\n" + java.util.Arrays.toString(data));
heapSort(data);
System.out.println("排序之后:\\n" + java.util.Arrays.toString(data));
}
}
2.交换排序
- ·冒泡排序(▲▲▲)
public class ExchangeSort_BubbleSort {
public static void main(String[] args) {
//交换排序-冒泡排序
int[] arr = new int[]{43,23,-67,54,66,26,88,-21,0,66};
//冒泡排序
//外层循环,代表数组内的所有元素需要几大轮进行比较才能比较完,是几大轮的意思
for(int i = 0;i < arr.length - 1;i++){
//内层循环,代表相邻的元素进行两两相比
for(int j = 0;j < arr.length - 1 - i;j++){
//判断相邻两个元素的大小
if(arr[j] > arr[j + 1]){
//如果前面元素比后面元素大,就进行交换,大的在后面
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
//遍历
for(int i = 0;i < arr.length;i++){
System.out.print(arr[i] + "\\t");
}
}
}
- ·快速排序(▲▲▲)
public class ExchangeSort_QuickSort {
private static void swap(int[] data, int i, int j) {
//交换排序-快速排序
/*通过一趟排序将待排序记录分割成独立的两部分,其中一部分记录的关键字均比另一部分关键字小,则分别对这两部分继续进行排序,直到整个序列有序。*/
int temp = data[i];
data[i] = data[j];
data[j] = temp;
}
private static void subSort(int[] data, int start, int end) {
if (start < end) {
int base = data[start];
int low = start;
int high = end + 1;
while (true) {
while (low < end && data[++low] - base <= 0)
;
while (high > start && data[--high] - base >= 0)
;
if (low < high) {
swap(data, low, high);
} else {
break;
}
}
swap(data, start, high);
subSort(data, start, high - 1);//递归调用
subSort(data, high + 1, end);
}
}
public static void quickSort(int[] data){
subSort(data,0,data.length-1);
}
public static void main(String[] args) {
int[] data = { 9, -16, 30, 23, -30, -49, 25, 21, 30 };
System.out.println("排序之前:\\n" + java.util.Arrays.toString(data));
quickSort(data);
System.out.println("排序之后:\\n" + java.util.Arrays.toString(data));
}
}
3.插入排序
- ·直接插入排序
public class InsertSort {
public static void insertSort(int[] data) {
//插入排序-直接插入排序
System.out.println("开始排序");
int arrayLength = data.length;
for (int i = 1; i < arrayLength; i++) {
int temp = data[i];
if (data[i] - data[i - 1] < 0) {
int j = i - 1;
for (; j >= 0 && data[j] - temp > 0; j--) {
data[j + 1] = data[j];
}
data[j + 1] = temp;
}
System.out.println(java.util.Arrays.toString(data));
}
}
public static void main(String[] args) {
int[] data = { 9, -16, 21, 23, -30, -49, 21, 30, 30 };
System.out.println("排序之前:\\n" + java.util.Arrays.toString(data));
insertSort(data);
System.out.println("排序之后:\\n" + java.util.Arrays.toString(data));
}
}
- ·折半插入排序
public class InsertSort_BinaryInsertSort {
public static void binaryInsertSort(int[] data) {
//插入排序-折半插入排序
System.out.println("开始排序");
int arrayLength = data.length;
for (int i = 1; i < arrayLength; i++) {
int temp = data[i];
int low = 0;
int high = i - 1;
while (low <= high) {
int mid = (low + high) / 2;
if (temp > data[mid]) {
low = mid + 1;
} else {
high = mid - 1;
}
}
for (int j = i; j > low; j--) {
data[j] = data[j - 1];
}
data[low] = temp;
System.out.println(java.util.Arrays.toString(data));
}
}
public static void main(String[] args) {
int[] data = { 9, -16, 21, 23, -30, -49, 21, 30, 30 };
System.out.println("排序之前:\\n" + java.util.Arrays.toString(data));
binaryInsertSort(data);
System.out.println("排序之后:\\n" + java.util.Arrays.toString(data));
}
}
- ·Shell排序
public class InsertSort_ShellSort {
public static void ShellSort(int[] data) {
//插入排序-Shell排序(希尔排序)
System.out.println("开始排序");
int arrayLength = data.length;
int h = 1;
while (h <= arrayLength / 3) {
h = h * 3 + 1;
}
while (h > 0) {
System.out.println("===h的值:" + h + "===");
for (int i = h; i < arrayLength; i++) {
int temp = data[i];
if (data[i] - data[i - h] < 0) {
int j = i - h;
for (; j >= 0 && data[j] - temp > 0; j -= h) {
data[j + h] = data[j];
}
data[j + h] = temp;
}
System.out.println(java.util.Arrays.toString(data));
}
h = (h - 1) / 3;
}
}
public static void main(String[] args) {
int[] data = { 9, -16, 21, 23, -30, -49, 21, 30, 30 };
System.out.println("排序之前:\\n" + java.util.Arrays.toString(data));
ShellSort(data);
System.out.println("排序之后:\\n" + java.util.Arrays.toString(data));
}
}
4.归并排序
public class MergeSort {
public static void mergeSort(int[] data) {
// 归并排序
sort(data, 0, data.length - 1);
}
// 将索引从left到right范围的数组元素进行归并排序
private static void sort(int[] data, int left, int right) {
if(left < right){
//找出中间索引
int center = (left + right)/2;
sort(data,left,center);
sort(data,center+1,right);
//合并
merge(data,left,center,right);
}
}
// 将两个数组进行归并,归并前两个数组已经有序,归并后依然有序
private static void merge(int[] data, int left, int center, int right) {
int[] tempArr = new int[data.length];
int mid = center + 1;
int third = left;
int temp = left;
while (left <= center && mid <= right) {
if (data[left] - data[mid] <= 0) {
tempArr[third++] = data[left++];
} else {
tempArr[third++] = data[mid++];
}
}
while (mid <= right) {
tempArr[third++] = data[mid++];
}
while (left <= center) {
tempArr[third++] = data[left++];
}
while (temp <= right) {
data[temp] = tempArr[temp++];
}
}
public static void main(String[] args) {
int[] data = { 9, -16, 21, 23, -30, -49, 21, 30, 30 };
System.out.println("排序之前:\\n" + java.util.Arrays.toString(data));
mergeSort(data);
System.out.println("排序之后:\\n" + java.util.Arrays.toString(data));
}
}
5.桶式排序
public class BucketSort {
public static void bucketSort(int[] data, int min, int max) {
//桶式排序
System.out.println("开始排序");
int arrayLength = data.length;
int[] temp = new int[arrayLength];
int[] buckets = new int[max - min];
for (int i = 0; i < arrayLength; i++) {
buckets[data[i] - min]++;
}
System.out.println(Arrays.toString(buckets));
for (int i = 1; i < max - min; i++) {
buckets[i] = buckets[i] + buckets[i - 1];
}
System.out.println(Arrays.toString(buckets));
System.arraycopy(data, 0, temp, 0, arrayLength);
for (int k = arrayLength - 1; k >= 0; k--) {
data[--buckets[temp[k] - min]] = temp[k];
}
}
public static void main(String[] args) {
int[] data = { 9, 5, -1, 8, 5, 7, 3, -3, 1, 3 };
System.out.println("排序之前:\\n" + Arrays.toString(data));
bucketSort(data, -3, 10);
System.out.println("排序之后:\\n" + Arrays.toString(data));
}
}
6.基数排序
public class MultiKeyRadixSort {
public static void radixSort(int[] data, int radix, int d) {
//基数排序
System.out.println("开始排序:");
int arrayLength = data.length;
int[] temp = new int[arrayLength];
int[] buckets = new int[radix];
for (int i = 0, rate = 1; i < d; i++) {
// 重置count数组,开始统计第二个关键字
Arrays.fill(buckets, 0);
// 当data数组的元素复制到temp数组中进行缓存
System.arraycopy(data, 0, temp, 0, arrayLength);
for (int j = 0; j < arrayLength; j++) {
int subKey = (temp[j] / rate) % radix;
buckets[subKey]++;
}
for (int j = 1; j < radix; j++) {
buckets[j] = buckets[j] + buckets[j - 1];
}
for (int m = arrayLength - 1; m >= 0; m--) {
int subKey = (temp[m] / rate) % radix;
data[--buckets[subKey]] = temp[m];
}
System.out.println("对" + rate + "位上子关键字排序:"
+ Arrays.toString(data));
rate *= radix;
}
}
public static void main(String[] args) {
int[] data = { 1100, 192, 221, 12, 13 };
System.out.println("排序之前:\\n" + Arrays.toString(data));
radixSort(data, 10, 4);
System.out.println("排序之后:\\n" + Arrays.toString(data));
}
}
理解
1.衡量排序算法的优劣
- 时间复杂度:分析关键字的比较次数和记录的移动次数
- 空间复杂度:分析排序算法中需要多少辅助内存
- 稳定性:若两个记录A和B的关键字值相等,但排序后A、B的先后次序保持不变,则称这种排序算法是稳定的
2.排序的分类
- 内部排序:整个排序过程不需要借助于外部存储器(磁盘等),所有排序操作都在内存中完成
- 外部排序:参与排序的数据非常多,数据量非常大,计算机无法把整个排序过程放在内存中完成,必须借助于外部存储器(磁盘等)。外部排序最常见的是多路归并排序,可以认为外部排序是由多次内部排序组成
3.不同排序算法的时间复杂度
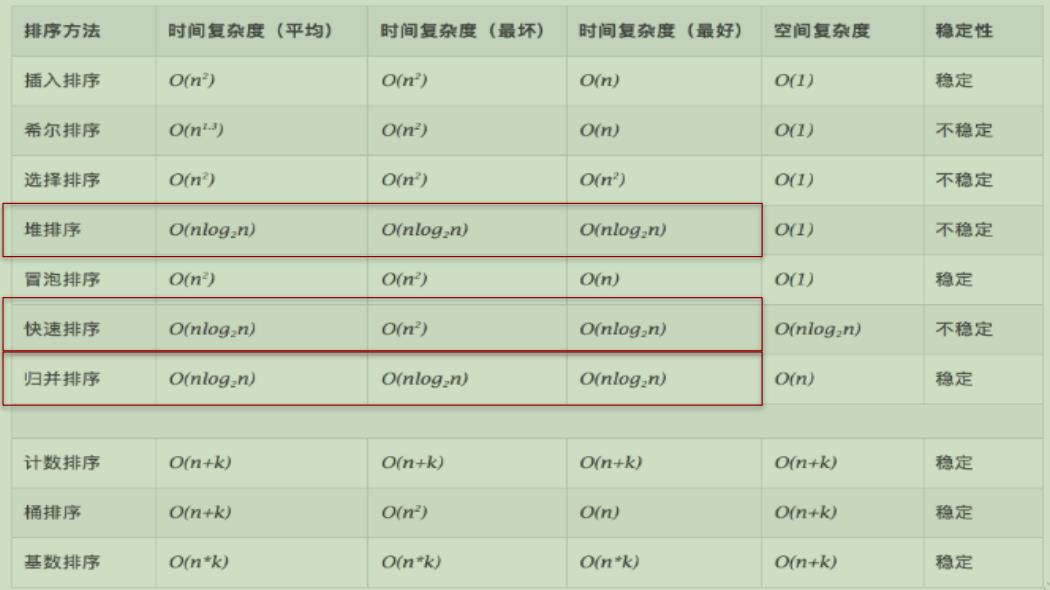
4.手写冒泡排序(▲▲▲)
int[] arr = new int[]{34,5,22,-98,6,-76,0,3};
//外层循环代表所有元素跑完一遍 需要几轮
for(int i = 0;i < arr.length;i++){
//内层循环代表 相邻元素两两比较
for(int j = 0;j < arr.length - 1 - i;j++){
if(arr[j] > arr[j + 1]){
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
for (int i = 0;i < arr.length;i++){
System.out.print(arr[i] + ",\\t");
}
以上是关于数组-数组的常见算法的主要内容,如果未能解决你的问题,请参考以下文章