机器学习sklearn（二十七）：模型评估量化预测的质量回归指标

Posted 2021-06-20 秋华

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了机器学习sklearn（二十七）：模型评估量化预测的质量回归指标相关的知识，希望对你有一定的参考价值。

该 sklearn.metrics 模块实现了一些 loss, score 以及 utility 函数以测量 regression（回归）的性能. 其中一些已经被加强以处理多个输出的场景: mean_squared_error, mean_absolute_error, explained_variance_score 和 r2_score.

这些函数有 multioutput 这样一个 keyword（关键的）参数, 它指定每一个目标的 score（得分）或 loss（损失）的平均值的方式. 默认是 \'uniform_average\', 其指定了输出时一致的权重均值. 如果一个 ndarray 的 shape (n_outputs,) 被传递, 则其中的 entries（条目）将被解释为权重，并返回相应的加权平均值. 如果 multioutput 指定了 \'raw_values\' , 则所有未改变的部分 score（得分）或 loss（损失）将以 (n_outputs,) 形式的数组返回.

该 r2_score 和 explained_variance_score 函数接受一个额外的值 \'variance_weighted\' 用于 multioutput 参数. 该选项通过相应目标变量的方差使得每个单独的 score 进行加权. 该设置量化了全局捕获的未缩放方差. 如果目标变量的大小不一样, 则该 score 更好地解释了较高的方差变量. multioutput=\'variance_weighted\' 是 r2_score 的默认值以向后兼容. 以后该值会被改成 uniform_average.

1. 解释方差得分

该 explained_variance_score 函数计算了 explained variance regression score（解释的方差回归得分）.

如果 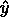$\\hat{y}$ 是预估的目标输出, 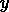是相应（正确的）目标输出, 并且 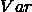Var is 方差, 标准差的平方, 那么解释的方差预估如下:

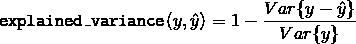
$\\texttt{explained\\_{}variance}(y, \\hat{y}) = 1 - \\frac{Var\\{ y - \\hat{y}\\}}{Var\\{y\\}}$

最好的得分是 1.0, 值越低越差.

下面是一下有关 explained_variance_score 函数使用的一些示例:

>>> from sklearn.metrics import explained_variance_score
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> explained_variance_score(y_true, y_pred)  
0.957...
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> explained_variance_score(y_true, y_pred, multioutput=\'raw_values\')
...
array([ 0.967...,  1.        ])
>>> explained_variance_score(y_true, y_pred, multioutput=[0.3, 0.7])
...
0.990...

2. 最大误差

max_error函数计算最大残差，该度量捕获预测值和真实值之间的最坏情况误差。在完全拟合的单输出回归模型中，训练集上的max_error将为0，尽管在现实世界中这是极不可能的，但是这个度量显示了模型在拟合时的误差程度。

如果 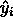$\\hat{y}_i$ 是 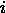-th 样本的预测值, 并且 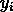y_i 是对应的真实值，则将最大误差定义为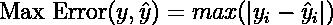 $\\text{Max Error}(y, \\hat{y}) = max(| y_i - \\hat{y}_i |)$

以下是max_error函数的一个示例：

>>> from sklearn.metrics import max_error
>>> y_true = [3, 2, 7, 1]
>>> y_pred = [9, 2, 7, 1]
>>> max_error(y_true, y_pred)
6

max_error不支持多输出

3. 平均绝对误差

该 mean_absolute_error 函数计算了平均绝对误差, 一个对应绝对误差损失预期值或者 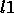-norm 损失的风险度量.

如果 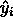$\\hat{y}_i$ 是 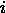-th 样本的预测值, 并且 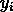y_i 是对应的真实值, 则平均绝对误差 (MAE) 预估的 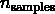$n_{\\text{samples}}$ 定义如下

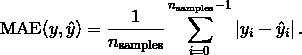
$\\text{MAE}(y, \\hat{y}) = \\frac{1}{n_{\\text{samples}}} \\sum_{i=0}^{n_{\\text{samples}}-1} \\left| y_i - \\hat{y}_i \\right|.$

下面是一个有关 mean_absolute_error 函数用法的小示例:

>>> from sklearn.metrics import mean_absolute_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_absolute_error(y_true, y_pred)
0.5
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> mean_absolute_error(y_true, y_pred)
0.75
>>> mean_absolute_error(y_true, y_pred, multioutput=\'raw_values\')
array([ 0.5,  1. ])
>>> mean_absolute_error(y_true, y_pred, multioutput=[0.3, 0.7])
...
0.849...

4. 均方误差

该 mean_squared_error 函数计算了均方误差, 一个对应于平方（二次）误差或损失的预期值的风险度量.

如果 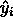$\\hat{y}_i$ 是 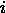-th 样本的预测值, 并且 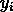y_i 是对应的真实值, 则均方误差（MSE）预估的 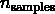$n_{\\text{samples}}$ 定义如下

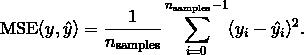
$\\text{MSE}(y, \\hat{y}) = \\frac{1}{n_\\text{samples}} \\sum_{i=0}^{n_\\text{samples} - 1} (y_i - \\hat{y}_i)^2.$

下面是一个有关 mean_squared_error 函数用法的小示例:

>>> from sklearn.metrics import mean_squared_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_squared_error(y_true, y_pred)
0.375
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> mean_squared_error(y_true, y_pred)  
0.7083...

示例

点击 Gradient Boosting regression 查看均方误差用于梯度上升（gradient boosting）回归的使用示例。

5. 均方误差对数

该 mean_squared_log_error 函数计算了一个对应平方对数（二次）误差或损失的预估值风险度量.

如果 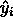$\\hat{y}_i$ 是 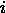-th 样本的预测值, 并且 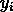y_i 是对应的真实值, 则均方误差对数（MSLE）预估的 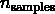$n_{\\text{samples}}$ 定义如下

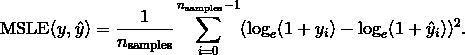
$\\text{MSLE}(y, \\hat{y}) = \\frac{1}{n_\\text{samples}} \\sum_{i=0}^{n_\\text{samples} - 1} (\\log_e (1 + y_i) - \\log_e (1 + \\hat{y}_i) )^2.$

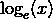其中 $\\log_e (x)$ 表示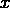的自然对数. 当目标具有指数增长的趋势时, 该指标最适合使用, 例如人口数量, 跨年度商品的平均销售额等. 请注意, 该指标会对低于预测的估计值进行估计.

下面是一个有关 mean_squared_log_error 函数用法的小示例:

>>> from sklearn.metrics import mean_squared_log_error
>>> y_true = [3, 5, 2.5, 7]
>>> y_pred = [2.5, 5, 4, 8]
>>> mean_squared_log_error(y_true, y_pred)  
0.039...
>>> y_true = [[0.5, 1], [1, 2], [7, 6]]
>>> y_pred = [[0.5, 2], [1, 2.5], [8, 8]]
>>> mean_squared_log_error(y_true, y_pred)  
0.044...

6. 中位绝对误差

该 median_absolute_error 函数尤其有趣, 因为它的离群值很强. 通过取目标和预测之间的所有绝对差值的中值来计算损失.

该 median_absolute_error 函数不支持多输出.

下面是一个有关 median_absolute_error 函数用法的小示例:

>>> from sklearn.metrics import median_absolute_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> median_absolute_error(y_true, y_pred)
0.5

7. R² score, 可决系数

该 r2_score 函数计算了 computes R², 即可决系数. 它提供了将来样本如何可能被模型预测的估量. 最佳分数为 1.0, 可以为负数（因为模型可能会更糟）. 总是预测 y 的预期值，不考虑输入特征的常数模型将得到 R^2 得分为 0.0.

如果 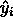$\\hat{y}_i$ 是 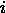-th 样本的预测值, 并且 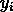y_i 是对应的真实值, 则 R² 得分预估的 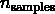$n_{\\text{samples}}$ 定义如下

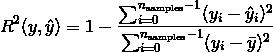
$R^2(y, \\hat{y}) = 1 - \\frac{\\sum_{i=0}^{n_{\\text{samples}} - 1} (y_i - \\hat{y}_i)^2}{\\sum_{i=0}^{n_\\text{samples} - 1} (y_i - \\bar{y})^2}$

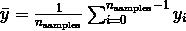其中 $\\bar{y} = \\frac{1}{n_{\\text{samples}}} \\sum_{i=0}^{n_{\\text{samples}} - 1} y_i$ .

下面是一个有关 r2_score 函数用法的小示例:

>>> from sklearn.metrics import r2_score
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> r2_score(y_true, y_pred)  
0.948...
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> r2_score(y_true, y_pred, multioutput=\'variance_weighted\')
...
0.938...
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> r2_score(y_true, y_pred, multioutput=\'uniform_average\')
...
0.936...
>>> r2_score(y_true, y_pred, multioutput=\'raw_values\')
...
array([ 0.965...,  0.908...])
>>> r2_score(y_true, y_pred, multioutput=[0.3, 0.7])
...
0.925...