python-堆排序
Posted 马上读初一
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了python-堆排序相关的知识,希望对你有一定的参考价值。
二叉树的顺序存储方式
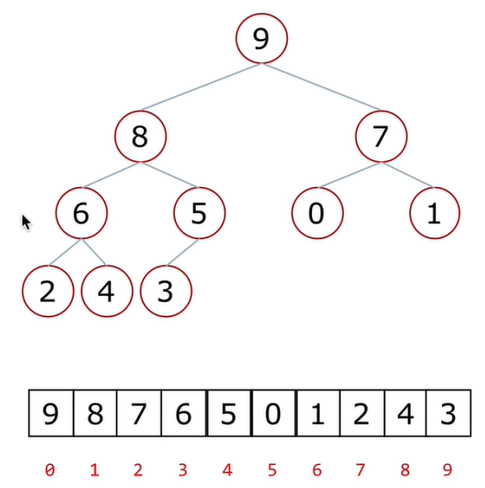
从上往下, 从左往右, 依次将元素追加至列表中, 可以得到如下规律:
-
父节点和左孩子节点的坐标关系为:
0-->1 1-->3 3-->7
即: i --> 2i+1
-
父节点和左孩子节点的坐标关系为:
0-->2 2-->6 1-->4 3-->7
即: i --> 2i+2
满二叉树与完全二叉树
满二叉树: 一个深度为k(>=-1)且有2^(k+1) - 1个结点的二叉树称为完美二叉树(满二叉树), 即每层节点数都满了
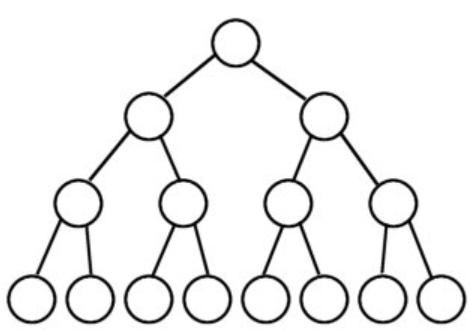
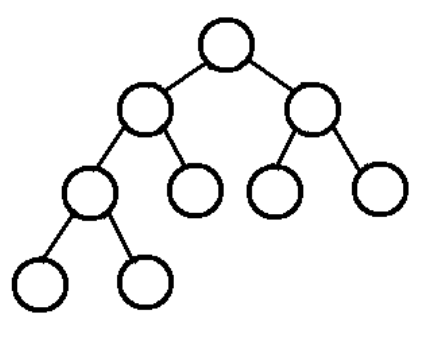
完全二叉树: 从根结点到倒数第二层满足完美二叉树(满二叉树),最后一层可以不完全填充,其叶子结点都靠左对齐。
堆
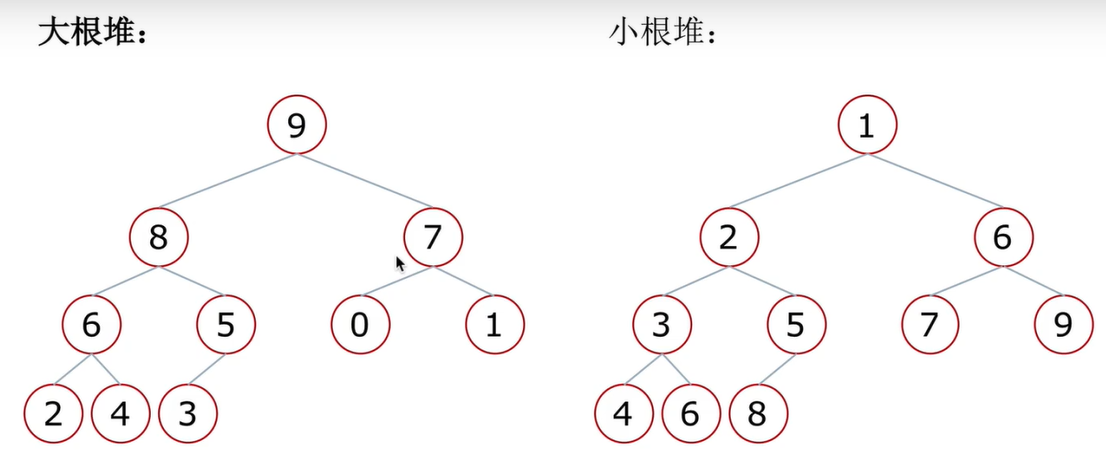
堆是一种特殊的完全二叉树结构, 堆分为大根堆和小根堆
- 大根堆: 一个完全二叉树, 且任一父节点的值都比孩子节点的值大
- 小根堆: 一个完全二叉树, 且任一父节点的值都比孩子节点的值小
向下调整的过程
一个自身并不是堆的完全二叉树(根节点的值并不比其孩子节点的值大), 但其左右子树都是堆
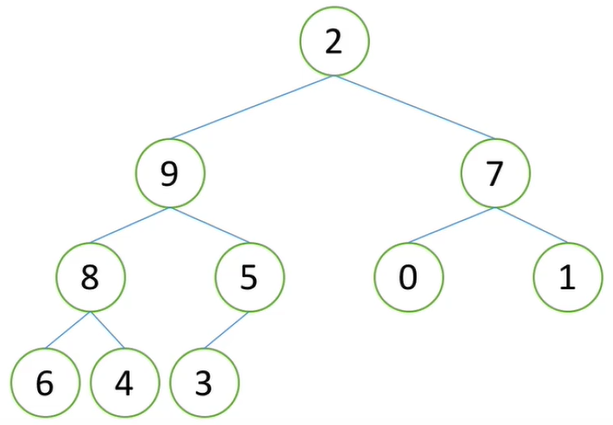
- 将第一层根元素(2)移出, 比较其左右孩子(9和7), 将较大者(9)移至原根元素(2)的位置, 此时原(9)的位置空出
- 将(2)和(9)的左右孩子(8和5)进行比较, 将较大者(8)移至原(9)的空位, 此时原(8)的位置空出
- 将(2)和(8)的左右孩子
- (6和4)进行比较, 将较大者(6)移至原(8)的空位, 此时原(6)的位置空出, 由于(6)下面没有孩子节点, 所以将(2)移至原(6)的空位
向下调整后:
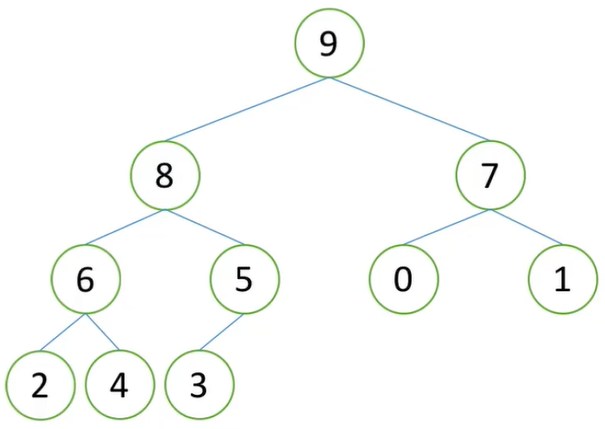
堆排序的过程
- 堆顶的元素肯定是堆中最大的元素, 因此拿到数组的最大值
- 将堆顶的元素(9)和堆最后一个元素(3)互换, 这样就形成了一个能够进行向下调整的二叉树
- 但是(9)这个元素已经取出过了, 它不应该还属于这个堆, 所以建立一个指针, 指向我们所需要用的堆的最后一个元素, 最开始指向(3)的位置, 当前面(9)和(3)互换之后, 就将该指针向左移动一位, 指向(4)的位置, 认为这个堆到(4)的位置结束, (9)不再属于这个堆, 只是在堆中占了一个位置而已.
- (9)和(3)互换后, 进行一个向下调整, 能够将堆中最大的(8)调整到堆顶的位置, 然后继续将(8)和堆中最后一位元素(4)进行互换, 再次进行向下调整
- 直到指针左移到最后一位元素. 排序也就结束了
构建堆的过程
前面将一个二叉树通过顺序存储方式存在一个列表中, 反过来, 可以将待排序列表按顺序构造成一个二叉树, 如列表:
[6, 8, 1, 9, 3, 0, 7, 2, 4, 5]
构造成二叉树就是:
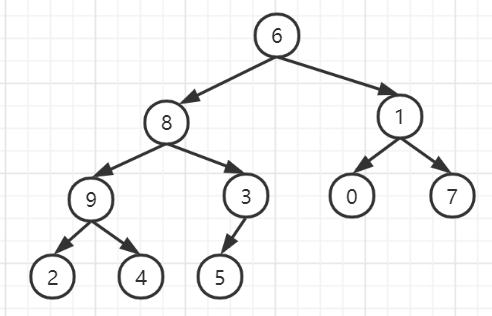
将二叉树构建成堆:
- 从下往上, 从右往左, 依次对每个父节点所在的子树进行一次向下调整
- 先对最末尾的父节点(3)的子树进行一次向下调整, 调整结果为(3)和(5)的位置进行互换
- 再对(9)的子树进行一次向下调整, 由于9>2和4, 所以不需要进行元素位移
- 再对(1)的子树进行向下调整, 结果为(7)和(1)位置互换
- 再对(8)子树进行向下调整, 由于其左子树和右子树都是堆, 所以可以满足向下调整的条件, 进行一次向下调整
- 再对根节点(6)进行向下调整, 最终将整个二叉树调整为了一个大根堆
最终形成的堆为:
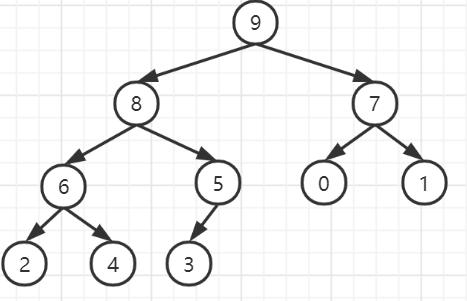
代码实现
向下调整
由于在构建堆和堆排序的过程中, 都需要用到向下调整, 所以我们先将向下调整的代码实现出来
最简单的向下调整
如调整前为:
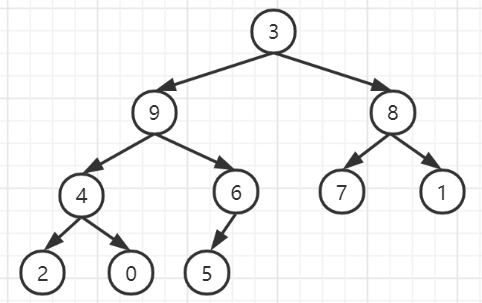
def shift(nums):
# 提取堆顶的值
i = 0
# 只要i有左孩子, 则继续循环
while 2*i+1 < len(nums):
# 提取i的左孩子
index_left = 2*i+1
value_left = nums[index_left]
# 提取i的右孩子
index_right = index_left+1
# 判断是否存在右孩子, 不存在则认为其值为-1
value_right = nums[index_right] if index_right < len(nums) else 0
# 比较当前值和左右孩子三者哪个大
# 若当前值大, 则无需进行调整, 结束循环
if nums[i] >= value_left and nums[i] >= value_right:
break
elif value_left >= value_right:
nums[i], nums[index_left] = nums[index_left], nums[i]
i = index_left
else:
nums[i], nums[index_right] = nums[index_right], nums[i]
i = index_right
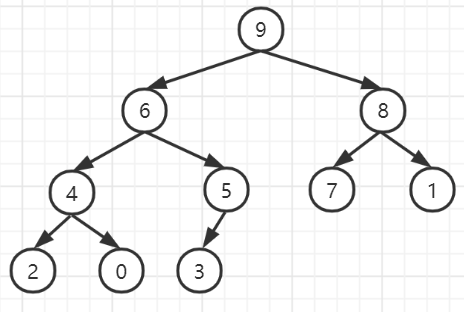
print(nums)
调整后结果为: [9, 6, 8, 4, 5, 7, 1, 2, 0, 3]
最终向下调整代码
上面的代码是针对一个完整的二叉树进行向下调整, 是从顶点开始的
而在构建堆的过程中, 是对二叉树的一部分子树依次进行向下调整的, 所以这个调整的父节点不能直接从顶点开始, 而是可以动态指定调整的父节点.
并且在堆排序的过程中, 由于我们是原地排序, 需要将顶点的位置和列表末尾的位置进行互换, 再进行向下调整, 然后末尾指针向前移动一位, 再和顶点位置进行互换, 继续向下调整, 直到排序完. 因此我们也需要动态指定调整的末尾节点.
因此添加两个参数, 依次指向调整的顶点和末尾节点
def shift(nums, top, low):
# 提取堆顶的值
i = top
# 只要i有左孩子, 则继续循环
while 2*i+1 <= low:
# 提取i的左孩子
index_left = 2*i+1
value_left = nums[index_left]
# 提取i的右孩子
index_right = index_left+1
# 判断是否存在右孩子, 不存在则认为其值为-1
value_right = nums[index_right] if index_right <= low else 0
# 比较左右孩子哪个大, 大者和i进行互换
# 若当前值大, 则无需进行调整, 结束循环
if nums[i] >= value_left and nums[i] >= value_right:
break
elif value_left >= value_right:
nums[i], nums[index_left] = nums[index_left], nums[i]
i = index_left
else:
nums[i], nums[index_right] = nums[index_right], nums[i]
i = index_right
print(nums)
堆排序完整代码
将一个数组进行堆排序的过程分为两步:
- 将数组构建成为一个堆
- 对这个堆进行排序
def heap_sort(nums):
# 建堆: 从最后一个父节点开始, 从右往左, 从下往上, 依次对父节点进行向下调整, 最终会构建成一个堆
# 父节点(下标i)的左孩子下标为2*i+1, 右孩子下标为2*i+2
# 左孩子和右孩子(下标j)的父节点(j-1)//2, 因此最后一个父节点坐标为(len(nums)-1-1)//2
for i in range((len(nums) - 1 - 1) // 2, -1, -1):
shift(nums, i, len(nums) - 1)
# 对堆进行排序: 将堆顶和堆尾进行互换, 再进行向下调整, 堆尾向前移动一位, 继续互换和调整, 知道指针指向堆顶
for i in range(len(nums)-1, -1, -1):
# 首位替换
nums[i], nums[0] = nums[0], nums[i]
# 进行向下调整
shift(nums, 0, i-1)
执行结果:
if __name__ == \'__main__\':
lst = [6, 8, 1, 9, 3, 0, 7, 2, 4, 5]
heap_sort(lst)
print(nums)
# 打印结果
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
以上是关于python-堆排序的主要内容,如果未能解决你的问题,请参考以下文章