矩阵乘法 —— 洛谷 P3193 [HNOI2008]GT考试

Posted 2021-06-14 绾纾

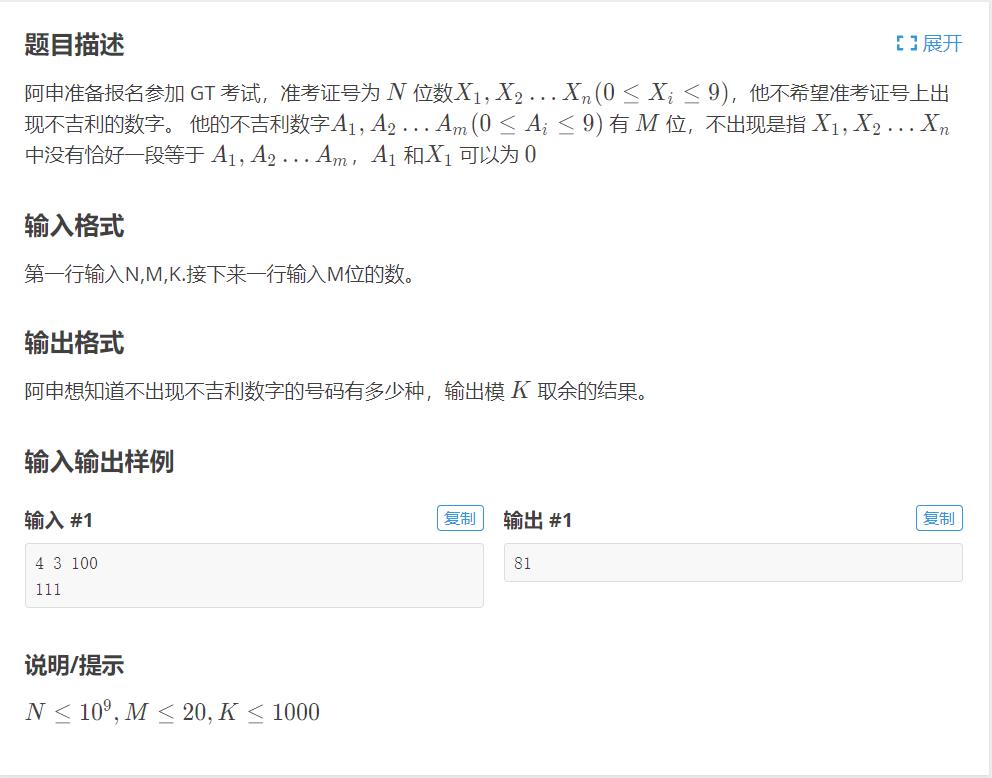
该题与\\(IndeedTokyo2019\\)校招笔试题涉及密码有相同的思路，都是\\(DP\\)问题。

思路

由于状态的数量众多，所以我们需要使用状态机模型考虑一大类状态的转移。

使用闫氏\\(DP\\)分析法，从集合角度分析问题：

• 状态表示：\\(f[i, j]\\)，表示长度为\\(i\\)且没有不吉利数字，且与不吉利数字匹配的最大前缀长度为\\(j\\)的所有字符串。所具有的属性为数量。
• 状态计算：我们从第\\(i\\)层转移到第\\(i+1\\)层需要在第\\(i\\)层后面添加上一个数字，而由于我们只关心与不吉利数字匹配的最大前缀长度和添加的数字，并不关心内部的数字，所以\\(f[i+1,k]=a _ {k0}f[i,0]+a _ {k1}f[i,1]+...\\)里的所有系数\\(a\\)都是不变的因此我们可以使用矩阵快速幂进行优化。

当我们计算中间矩阵\\(a\\)时，矩阵乘法公式\\(f[i+1,k]=\\sum^{m-1} _ {j=0}f[i,j] * a[j,k]\\)，我们我们只需要知道\\(^{[1]}\\)不吉利数字的长度为\\(j\\)的前缀加上数字\\(0-9\\)之后能转移到哪个长度\\(k\\)，然后使\\(a[j,k]+1\\)即可。

\\([1]\\)：可以使用\\(KMP\\)来辅助优化。
优化思路：\\(ne[j]=k\\)表示下标为\\(j\\)的前面\\(k\\)个字符与前缀的\\(k\\)个字符相同，即表示当第\\(j\\)个字符不匹配时指针将要移动到的位置。所以我们要使第\\(j\\)个字符之后加上一个数字后与某个长度匹配，只需要使\\(k=j+1\\)，表示前\\(j\\)个字符都已经匹配，当第\\(k\\)个字符不等于加上的数字时再移动指针，当指针不移动时就表示已经匹配到了一个长度为\\(k\\)的前缀，使\\(a[j,k]+1\\)即可。

代码

const int N = 25;

int a[N][N], ne[N];
char str[N];
int n, m, mod;

void mul(int c[][N], int a[][N], int b[][N]) 
{
    static int temp[N][N];
    memset(temp, 0, sizeof temp);
    
    for (int i = 0; i < m; i ++ ) 
        for (int j = 0; j < m; j ++ ) 
            for (int k = 0; k < m; k ++ ) 
                temp[i][j] = (temp[i][j] + a[i][k] * b[k][j]) % mod;
    memcpy(c, temp, sizeof temp);
}

int qpow() 
{
    int F[N][N] = {1};
    while (n) 
    {
        if (n & 1) mul(F, F, a);
        mul(a, a, a);
        n >>= 1;
    }
    
    int res = 0;
    for (int i = 0; i < m; i ++ ) res = (res + F[0][i]) % mod;
    return res;
}

int main() 
{
    cin >> n >> m >> mod;
    cin >> str + 1;
    
    // kmp匹配ne数组
    int j = 1, k = 0;
    ne[j] = k;
    while (j <= m) 
    {
        if (k == 0 || str[j] == str[k]) j ++ , k ++ , ne[j] = k;
        else k = ne[k];
    }
    
    // kmp初始化a数组
    for (int j = 0; j < m; j ++ ) 
        for (int c = \'0\'; c <= \'9\'; c ++ ) 
        {
            int k = j + 1;
            while (k && str[k] != c) k = ne[k];
            if (k < m) a[j][k] ++ ;
        }
        
    cout << qpow() << endl;
    
    return 0;
}