Szkopul (rek). Task Recursive Ant

Posted 2021-06-14 Neal_lee

题目链接

Szkopul Task Recursive Ant (rek)

题目大意

有一张 \\(2^n\\times2^n\\) 的网格图，其中有 \\(m\\) 的格子有障碍无法到达，从 \\((0,0)\\) 即左上角的格子开始，每次移动到相邻的一个无障碍且未被访问的格子，移动的路径有以下要求：

对于当前处在的一个 \\(2^k\\times2^k(k\\geq 1)\\) 的区块内，它由四个 \\(2^{k-1}\\times2^{k-1}\\) 更小的区块组成，你需要依次把每个块完整访问一遍，即进入一个块之后，需要把其内所有无障碍格子都走一遍，然后才可以离开这个区域。

现在问是否能够最终分别从网格图的四个边界离开网格图，若一个方向可以，则输出一个可行的最终离开格子的坐标，否则输出 NIE（波兰语的 NO）。输出的顺序是 ”上右下左“ 。

\\(0\\leq n\\leq 30\\), \\(0\\leq m\\leq 50\\)

思路

注意到 \\(m\\leq 50\\) 和 \\(2^n\\leq 2^{30}\\) 的数量级差的很大，那应该就可以想到我们要对 \\(m\\) 个障碍有关的事物专门处理，而其它没有障碍的部分是可以很快地得到结果的。

先考虑如何快速地得到无障碍部分的结果。

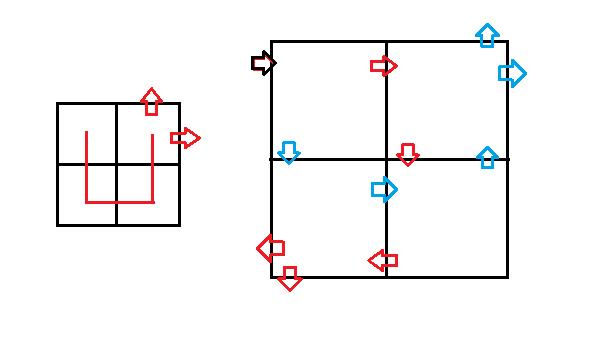
如果直接从左上角进入，可以发现是从「从右上到左下的对角线」的两侧离开该区域的，这一点用数学归纳法的思路很容易进行严谨证明。注意左图中 \\(2\\times2\\) 的基础图形，它只有从上面一格开始走和从下面一格开始走两种情况，如果从 \\((1,0)\\) 进入，那就是从离对角线（后文的对角线都指之前定义的那个）距离 \\(1\\) 的格子离开，从而如果我们在左侧从任意一个位置进入网格图，这个位置可以进行类似于二进制拆解的思路，对应到基础情况中的从上面走还是从下面走，最终可以得出一个结论（此处可以手画一画，更明确的感知一下）：当进入的位置离 \\((0,0)\\) 为 \\(d\\) 时，我们最终会从离对角线 \\(d\\) 的地方（共 \\(4\\) 个）离开此区域。

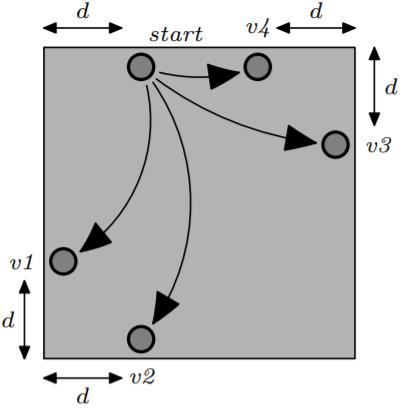
所以我们知道进入的位置时，可以 \\(O(1)\\) 地得到它最终所有可以离开的位置。

 

而对于有障碍物的格子，它们好像很难有什么规律，那么我们对所有包含障碍物的区域都暴力计算即可，这样的区域数量是 \\(O(nm)\\) 级别的（最多嵌套 \\(n\\) 层）。于是我们可以递归处理原问题，对于当前 \\(2^k\\times2^k\\) 的块，如果它不包含障碍，直接 \\(O(1)\\) 返回所有可行的出口（根据之前的分析可以知道这个出口数量 \\(\\leq 4\\)），否则分别递归 \\(4\\) 个 \\(2^{k-1}\\times2^{k-1}\\) 的块，将块块之间组合，枚举两种遍历方式（即遍历 \\(2\\times2\\) 可以有的那两种），即可以得到当前块的答案了。

时间复杂度：\\(O(nm)\\)

 

实现

上面的思路说的轻巧，但这个东西实现起来还挺难的，因此专门讲讲怎么实现。

我们需要实现一个函数 solve(x, y, len, k)，目前在考虑左上角坐标为 \\((x,y)\\)，边长为 \\(len\\) 的区域，含有障碍的区域其规律很难把控，我们只求当输入为 \\(k\\) 时它最终可以离开的格子位置，称其为输出。

输入和输出都是在边界的地方进行的，由之前的分析可以知道它们与「从右上到左下的对角线」有关，这里定义一个结构体 struct io{ int dir, dis; }; 表示这个输入/输出位置的方向为 dir，顺序与最终输出答案的方向顺序相同，这个位置离对角线的距离为 dis，为了方便这里 dis 的范围是 \\([1,2^k]\\) 。

solve 函数要返回一系列输出，所以输出类型为 vector<io> ，若此区域无障碍，直接计算结果即可。

bool exist(int x0, int y0, int x1, int y1){
	rep(i,0,m-1)
		if(x[i] >= x0 && x[i] <= x1 && y[i] >= y0 && y[i] <= y1)
			return true;
	return false;
}
....
vector<io> ret;
if(!exist(x, y, x+len-1, y+len-1)){
	rep(i,0,3) ret.push_back({i, len-k.dis+1});
	return ret;
}

若此区域全被障碍填满了，那也不需要在讨论了，直接返回空 vector。

bool filled(int a, int b, int len){
	if((len >= 8) || len*len > m) return false;
	int cnt = 0;
	rep(i,0,m-1)
		if(x[i] >= a && x[i] < a+len && y[i] >= b && y[i] < b+len) cnt++;
	return cnt == len*len;
}
...
if(filled(x, y, len)) return {};

注意 filled 函数要判一下 len 是否 \\(\\geq 8\\)，否则直接相乘可能会 int 溢出。

接下处理一般性的情况，这里我们有两种行走的方式，而不同的方式里小方块之间输入输出不相同，还与传进来的输入有关，如果直接分类讨论，那么可能会非常复杂。考虑这里再实现一个函数 go(x, y, dir, len, k)，表示从 \\((x,y,len)\\) 的那个方块开始，k 为它的初始输入，按照 dir 的方向进行一系列游走，这里 dir 是一个 vector<int>，在此情况最终的所有输出。

先假设 go 函数已经写好了，这里我们再讨论一下当前是从那个方位的方块开始的，然后把 go 函数两种游走方式下的输出合并即可，由于这里合并要去重，我实现了一个 map<io, bool>，并为 io 定义了大小比较关系：

struct io{ 
	int dir, dis;
	bool operator < (const io b) const{ 
		if(dir != b.dir) return dir < b.dir;
		return dis < b.dis;
	}
};
map<io, bool> vis;
....
    
vector<io> a, b;
if((k.dir == 0 || k.dir == 3) && k.dis > len/2){
	k.dis -= len/2;
	a = go(x, y, len/2, {1, 2, 3}, k), b = go(x, y, len/2, {2, 1, 0}, k);
}
else if((k.dir == 0 || k.dir == 1) && k.dis <= len/2)
	a = go(x, y+len/2, len/2, {3, 2, 1}, k), b = go(x, y+len/2, len/2, {2, 3, 0}, k);
else if((k.dir == 1 || k.dir == 2) && k.dis > len/2){
	k.dis -= len/2;
	a = go(x+len/2, y+len/2, len/2, {3, 0, 1}, k), b = go(x+len/2, y+len/2, len/2, {0, 3, 2}, k);
}
else if((k.dir == 2 || k.dir == 3) && k.dis <= len/2)
	a = go(x+len/2, y, len/2, {0, 1, 2}, k), b = go(x+len/2, y, len/2, {1, 0, 3}, k);

vis.clear();
for(io p : a) if(!vis[p]) ret.push_back(p), vis[p] = true;
for(io p : b) if(!vis[p]) ret.push_back(p), vis[p] = true;

 

接下来考虑实现 go(x, y, dir, len, k) ，这里有一个麻烦的地方，就是当这 \\(4\\) 个方块中有一些被完全填上的时候，我们是不用走它的，这使最终的输出的方向并不好确定，我还需要知道最后一个走的块的方位（\\(2\\times2\\)）是什么。

于是我们先处理出这个起始方块的方位，这一点可以通过 dir 还原出来，看前两步是咋走的即可。

int X[4] = {-1, 0, 1, 0}, Y[4] = {0, 1, 0, -1};
...
int a = 0, b = 0;
rep(i,0,1) a += X[dir[i]], b += Y[dir[i]];
a = (a < 0), b = (b < 0);

然后我们一步步去走，每次把上一步的输出转化成输出传给下一个块的 solve，然后根据游走实际所需的方向，保留那个需要的输出，如果没有则说明此次游走是不可能达成的，直接返回空 vector。而如果发现下一个块被障碍完全填满了，这意味着我们的行程就要到此为止了，检查一下再后面的方块是否也被填满了，没填满（那我们也没法访问了）就返回空 vector。

用 \\((a,b)\\) 实时记录当前块的方位，最后需要根据这个实际方位去找合适的输出，这个合适的输出为了避免分类讨论，这里用数组预处理出来

int ch[2][2][2] = {
	{{0, 3}, {0, 1}},
	{{2, 3}, {1, 2}}
};

前两位是方位 \\((a,b)\\)，第三维放两种可行的方向。

注意最后返回输出的时候，输出要转化成大方块的格式，所以还需根据方位的确定 dis 是否需要加上一个 len 。最终 go 函数的实现如下：

vector<io> go(int x, int y, int len, vector<int> dir, io k){
	int a = 0, b = 0;
	rep(i,0,1) a += X[dir[i]], b += Y[dir[i]];
	a = (a < 0), b = (b < 0);

	rep(i,0,2){
		vector<io> tmp = solve(x, y, len, k);
		bool flag = false;
		io tmpk = k;
		for(io p : tmp) if(p.dir == dir[i]) k = p, flag = true;
		if(!flag) return {};

		if(k.dir >= 2) k.dir -= 2;
		else k.dir += 2;
		k.dis = len-k.dis+1;
		x += X[dir[i]]*len, y += Y[dir[i]]*len;
		a += X[dir[i]], b += Y[dir[i]];

		if(filled(x, y, len)){
			int tmpx = x-X[dir[i]]*len, tmpy = y-Y[dir[i]]*len;
			rep(j,i+1,2){
				x += X[dir[j]]*len, y += Y[dir[j]]*len;
				if(!filled(x, y, len)) return {};
			}
			x = tmpx, y = tmpy, k = tmpk;
			a -= X[dir[i]], b -= Y[dir[i]];
			break;
		}
	}
	vector<io> tmp = solve(x, y, len, k), ret;
	for(io p : tmp)
		if(p.dir == ch[a][b][0] || p.dir == ch[a][b][1])
			ret.push_back(p);
	int id = a^b^1;
	rep(i,0,(int)ret.size()-1) ret[i].dis += id*len;
	return ret;
}

 

然而事情还没有结束，回到 solve 函数，由于有大量二选一的操作，边长为 \\(2^k\\) 的块下面最差要做 \\(2^k\\) 次决策，但是它们中只有 \\(O(1)\\) 不同的情况（因为只有方向会有变化，相对对角线的位置是不变的），对 solve 的操作进行记忆化，记 struct state{ int a, b, c; io d; } 为一个状态，给它定义大小比较之后塞 map 里面即可。

然后基本上就可以得到完整的代码了，由于要 map 记忆化，实际实现的时间复杂度是 \\(O(nm\\log(nm))\\) 的，把它换成哈希就可以达到理论复杂度了。

 

Code

#include<iostream>
#include<vector>
#include<cstring>
#include<map>
#define mem(a,b) memset(a, b, sizeof(a))
#define rep(i,a,b) for(int i = (a); i <= (b); i++)
#define per(i,b,a) for(int i = (b); i >= (a); i--)
#define N 55
using namespace std;

int n, m;
int x[N], y[N];
int X[4] = {-1, 0, 1, 0}, Y[4] = {0, 1, 0, -1};
int ch[2][2][2] = {
	{{0, 3}, {0, 1}},
	{{2, 3}, {1, 2}}
};
int end_x[4], end_y[4];

struct io{ 
	int dir, dis;
	bool operator < (const io b) const{ 
		if(dir != b.dir) return dir < b.dir;
		return dis < b.dis;
	}
};
struct state{
	int a, b, c;
	io d;
	bool operator < (const state bb) const{ 
		if(d < bb.d || bb.d < d) return d < bb.d;
		if(a != bb.a) return a < bb.a;
		if(b != bb.b) return b < bb.b;
		return c < bb.c;
	}
};
map<io, bool> vis;
map<state, vector<io> > f;

bool exist(int x0, int y0, int x1, int y1){
	rep(i,0,m-1)
		if(x[i] >= x0 && x[i] <= x1 && y[i] >= y0 && y[i] <= y1)
			return true;
	return false;
}
bool filled(int a, int b, int len){
	if((len >= 8) || len*len > m) return false;
	int cnt = 0;
	rep(i,0,m-1)
		if(x[i] >= a && x[i] < a+len && y[i] >= b && y[i] < b+len) cnt++;
	return cnt == len*len;
}

vector<io> solve(int x, int y, int len, io k);

vector<io> go(int x, int y, int len, vector<int> dir, io k){
	int a = 0, b = 0;
	rep(i,0,1) a += X[dir[i]], b += Y[dir[i]];
	a = (a < 0), b = (b < 0);

	rep(i,0,2){
		vector<io> tmp = solve(x, y, len, k);
		bool flag = false;
		io tmpk = k;
		for(io p : tmp) if(p.dir == dir[i]) k = p, flag = true;
		if(!flag) return {};

		if(k.dir >= 2) k.dir -= 2;
		else k.dir += 2;
		k.dis = len-k.dis+1;
		x += X[dir[i]]*len, y += Y[dir[i]]*len;
		a += X[dir[i]], b += Y[dir[i]];

		if(filled(x, y, len)){
			int tmpx = x-X[dir[i]]*len, tmpy = y-Y[dir[i]]*len;
			rep(j,i+1,2){
				x += X[dir[j]]*len, y += Y[dir[j]]*len;
				if(!filled(x, y, len)) return {};
			}
			x = tmpx, y = tmpy, k = tmpk;
			a -= X[dir[i]], b -= Y[dir[i]];
			break;
		}
	}
	vector<io> tmp = solve(x, y, len, k), ret;
	for(io p : tmp)
		if(p.dir == ch[a][b][0] || p.dir == ch[a][b][1])
			ret.push_back(p);
	int id = a^b^1;
	rep(i,0,(int)ret.size()-1) ret[i].dis += id*len;
	return ret;
}

vector<io> solve(int x, int y, int len, io k){
	vector<io> ret, a, b;
	if(!exist(x, y, x+len-1, y+len-1)){
		rep(i,0,3) ret.push_back({i, len-k.dis+1});
		return ret;
	}
	if(filled(x, y, len)) return {};
	if(f.count({x, y, len, k})) return f[{x, y, len, k}];

	int tmp = k.dis;
	if((k.dir == 0 || k.dir == 3) && k.dis > len/2){
		k.dis -= len/2;
		a = go(x, y, len/2, {1, 2, 3}, k), b = go(x, y, len/2, {2, 1, 0}, k);
	}
	else if((k.dir == 0 || k.dir == 1) && k.dis <= len/2)
		a = go(x, y+len/2, len/2, {3, 2, 1}, k), b = go(x, y+len/2, len/2, {2, 3, 0}, k);
        
	else if((k.dir == 1 || k.dir == 2) && k.dis > len/2){
		k.dis -= len/2;
		a = go(x+len/2, y+len/2, len/2, {3, 0, 1}, k), b = go(x+len/2, y+len/2, len/2, {0, 3, 2}, k);
	}
	else if((k.dir == 2 || k.dir == 3) && k.dis <= len/2)
		a = go(x+len/2, y, len/2, {0, 1, 2}, k), b = go(x+len/2, y, len/2, {1, 0, 3}, k);
	
	vis.clear();
	for(io p : a) if(!vis[p]) ret.push_back(p), vis[p] = true;
	for(io p : b) if(!vis[p]) ret.push_back(p), vis[p] = true;
	k.dis = tmp;
	return f[{x, y, len, k}] = ret;
}

int main(){
	cin>>n>>m;
	rep(i,0,m-1) cin>>x[i]>>y[i];
	
	vector<io> ans = solve(0, 0, 1<<n, {0, 1<<n});
	mem(end_x, -1), mem(end_y, -1);
	for(io k : ans){
		int a, b;
		switch(k.dir){
			case 0 : a = 0, b = (1<<n)-k.dis; break;
			case 1 : a = k.dis-1, b = (1<<n)-1; break;
			case 2 : a = (1<<n)-1, b = k.dis-1; break;
			case 3 : a = (1<<n)-k.dis, b = 0; break;
		}
		end_x[k.dir] = a, end_y[k.dir] = b;
	}
	rep(i,0,3){
		if(~end_x[i]) cout<<end_x[i]<<" "<<end_y[i]<<endl;
		else puts("NIE");
	}
	return 0;
}