StyleGan

Posted 2021-06-13 大草原

虽然很多人写过关于StyleGan的帖子，为了加深自己的理解，决定再啰嗦一遍。

StyleGan生成器

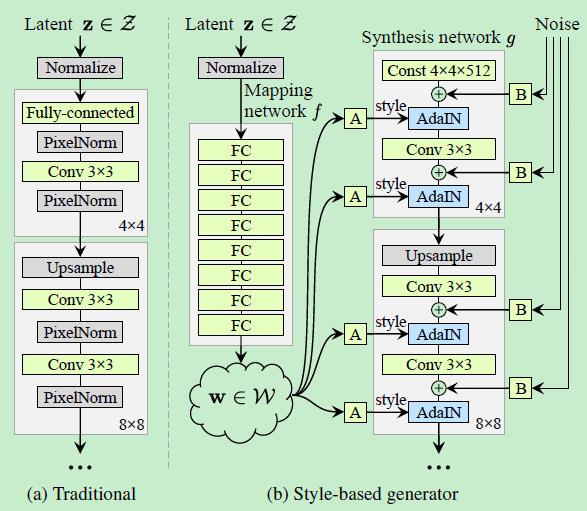
这部分用来介绍StyleGan生成器网络结构图。示意图如下

（1）传统的Gan生成器，由latent code 作为输入，生成图片。而StyleGan却是由一个常量通过生成网络生成图片的。而在StyleGan中latent code 经过一个多层感知器MLP，将隐特征空间Z映射到另一个隐特征空间W，\\(f: Z -> W\\),后续部分将会介绍这样做，可以实现latent code尽可能地特征解耦合，从而实现不同粗细力度图片生成和图片不同属性的生成。

（2）生成网络结构中，共计包括\\(4^2 - 1024^2\\)共计9个不同分辨率模块。除了最开始\\(4^2\\)模块，只有一个conv层，其他分辨率的都是有2个conv层，每个conv层之后，都加入随机噪声，当然是经过学习后的尺度因子映射B后的再相加的。

（3）上述（1）中提到的原始latent code经过映射后得到的中间层latent code，实际就是从训练集中学习到的图片中间层隐空间分布一个实例。经过学习到的仿射变换和自适应实例正则化AdaIN，将学习到的风格Style传递下去。

（4）文中提到了style一词，这个是从style transfer相关论文延续下来的，不过StyleGan中并不是从原始图片中计算style而是，而是从中间w计算出来的空间不变的style：y

（5）stylegan中一个重要的操作是AdaIN，是实例正则化操作，有别于BN，只针对单个样本进行处理。设\\(x_i\\)为第i个特征图，\\(y=(y_s,y_b)\\)是计算得到的style。这个操作也是逐通道处理的，因此y特征维度是x特征图通道数的2倍。

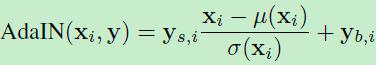
（在写这个帖子前，我不看论文画出StyleGan的网络结构示意图，我试了一下，画不出来。这也是我花时间写这些的意义所在。你以为你很懂了，其实可能还差很多。）

3. StyleGan生成器特点

StyleGan网络结构由左侧的映射网络mapping network和右侧的合成网络systhesis network构成，左侧mapping network和仿射变换A 相当于为学习过的分布中的每一种style 取样；而右侧的systhesis network相当于可以为学习过的各种styles生成图像。The effects of each style are localied in the network. 这句话该如何理解？根据文中表述和下面解释，每个style产生的影响只是影响图像中的某些方面。我想补充的是，其实从\\(4^2 - 1024^2\\)从低分辨率到高分辨率过程中，每个style都产生影响，后面的style产生的影响是在前面的基础上，继承前style的特点，不会大范围的改变，而是小范围的局部的改变。比如前面style已经确定了生成人物图片ID，头部姿态，那么后面的style基本不会改变这些，而是影响人物的发型，是否佩戴眼镜，表情等。

为什么会产生这种效果呢？因为采用AdaIN操作，该操作是对特征图逐通道减均值，除以方差，然后应用当前style的scale & bias，每此conv操作之后都进行该项操作。从\\(4^2 - 1024^2\\)从低分辨率到高分辨率过程中，每个分辨率都包括2个AdaIN操作，消除了部分原始统计特征，因此每个style就影响当前模块，表现在图像中就是影响局部特征或某些方面属性。

3.1 style mixing

style mixing 是指在训练过程中不再是使用一个latentcode而是使用多个latent code生成图片。比如latent code \\(z_1, z_2\\)生成中间latent code\\(w_1,w_2\\),为了合成新的图片是混合着使用\\(w_1,w_2\\)，对比着StyleGan 合成网络结构，在一些节点使用\\(w_1\\)，而剩余的使用\\(w_2\\)。这样做的目的是为了防止前后style产生依赖关系，亦是增强style的local特点。

文中Fig3展示了style混合的特点，而且从图片中也可以看出在不同尺度的style改变，对图片不同属性的影响。如下图所示，第一列代表Source A，第1行代表Source B。不管是A还是B都是由不同的latent code生成的。图片中剩余的混合使用组合Source A和Source B对于latent code生成的中间latent code w得到。

图片中第2行-第4行是在尺度\\(4^2-8^2\\)使用Source B对应w，剩余的是使用SourceA对应的w；图片中第5行-第6行是在度\\(16^2-32^2\\)使用Source B对应w，剩余的是使用SourceA对应的w；图片中第7行是在度\\(64^2-1024^2\\)使用Source B对应w，剩余的是使用SourceA对应的w；

首先从\\(4^2-1024^2\\)过程中，可以看着生成图片是由粗力度到细力度，从图片中可以看出来。\\(64^2-1024^2\\)这部分使用SourceB部分，但是生成的图片改变较少，主要图片的颜色和微小细节。而在\\(4^2-8^2\\)这部分，使用Source B的style，则人物的角度姿态、脸型、性别、年龄、眼镜等特征发生了改变与Source B]保持一致，但是肤色却没有改变。

随机变化

首先人的头发位置、毛孔、雀斑位置等这些都是随机，所以在生成人物图像的这些属性也应该具有随机性，只要其分别符合真实的分布。传统的生成器，是在网络中生成位置无关的伪随机数，生成的方式来自之前层的激活值。但是这种方式经常失效，会在图片中出现重复的模式。而StyleGan这种方式则极大改善了这个问题。

下图Fig4展示了加入随机噪音主要产生发型位置微小的改变。通过（c）标准方差图可以看到脸部较暗（基本没有变化），头发部分较亮（变化的就是头发区域），即使是这些也是微小的变化，没有引起图片感知上的很大变化。

下图Fig5则展示在不同尺度上加入随机噪音，对图片内容产生的影响。（a）是在各个尺度上都加入噪声，（b）是一点噪声都没有加，（c）是在\\(64^2-1024^2\\)尺度上加，（d）是在\\(4^2-8^2\\)尺度上添加。可以明显看到没有加入任何噪音的，丢失了更细节的信息，而仅在粗力度尺度上加入噪声，则产生更大更粗的发卷，而在细力度尺度上则产生的是更细小更密集的发卷。而全尺度上则是介于中间。这幅图片也进一步验证了从\\(4^2-1024^2\\)过程中，将产生由粗到细的改变。粗的可能是脸型、头部姿态、性别等，细的可能是发型、头发位置等。

Disentanglement studies

解耦学习的目的是学习的特征空间线性可分，可以由多个线性对的子空间构成。每个线性子空间控制变化的一个方面。
为了比较解耦效果，需要一种度量方式来衡量。本文介绍了两种，一个是感知路径，一个

感知路径

那什么是解耦效果好坏呢？假设z1，z2是隐特征空间中任意两个latentcode，分别生成两张图片，如果对这两个
latent code进行线性插值生成z，如果由该latent code生成的图像，和之前两张图像有很大差异，出现了之前两张图像没有呈现出的图像特征。如果发生了这种情况，则表明隐特征空间是耦合的，变化的影响因素没有合适的拆分。为了量化这种影响，通过测量插值后图像的变化差异来衡量。

一种基本的方法是感知路径，通过测试两张图片特征之间的加权插值来衡量，权重是通过拟合人的感知而获得到。
而衡量隐特征空间的解耦合程度，是将特征空间拆分成多个子空间，累加子空间感知路径，求其极限作为特征空间感知
路径值。然后实际上操作很困难，于是通过随机取特征空间中任意两个latentcode，按t取插值z，再按t+epsion取插值，然后求由这两个插值latent生成图像的感知路径的期望。数学公式表达如下：

\\(l_z = E[\\frac{1}{{\\epsilon}^2}d(G(slerp(z_1,z_2,t)), G(slerp(z_1,z_2,t+\\epsilon)))]\\)

其中slerp为球面插值，因为z向量都是单位长度。而中间隐特征空间W，是经过network mapping映射得到的，中间层特征向量w不一定是单位长度，因此衡量中间层隐特征空间的解耦程度，就不能使用球面插值，只能采用常用的线性插值。

\\(l_w = E[\\frac{1}{{\\epsilon}^2}d(G(lerp(w_1,w_2,t)), G(lerp(w_1,w_2,t+\\epsilon)))]\\)

Linear Seperability

隐特征空间线性可分，则可以找到一个线性超平面可以将隐空间分成两个部分，分属两侧则对应图像的二值属性。使用Celeba-HQ属性数据集训练属性分类器，比如性别分类。 随机取\\(z ~ P(z)\\)生成20000张图片，然后用训练好的属性分类器对生成的图片进行属性预测，选择性别置信度最高的一半样本即10000张图片。这样就得到了10000组（z，label_gender），然后训练出一个SVM。设X为属性分类器预测的属性类别X，Y是SVM预测的属性类别Y，定义条件熵H(X|Y)。该条件熵说明，在知道当前样本位于SVM超平面哪一侧的情况下，还需要多少额外条件，才能确定当前样本真实类别（Y）