二逼平衡树

Posted 2021-06-13 XIN

对，你没看错，题目就这。。。

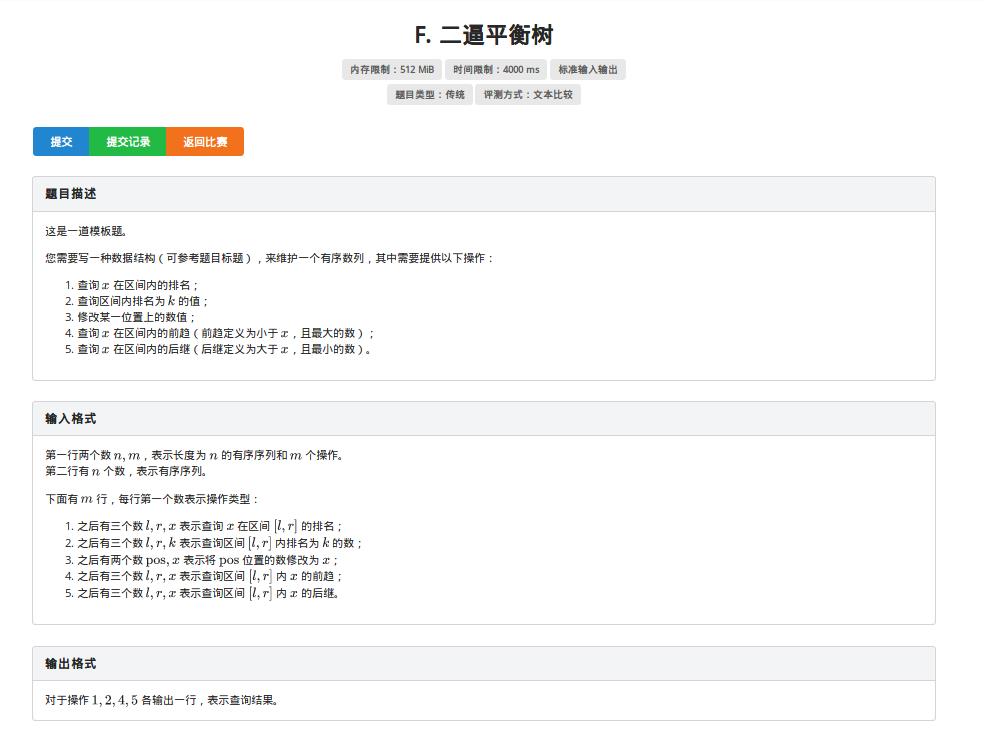
一眼看上去，似乎是个和之前一样的板子，然后再一看。。。

---

...为啥还有区间要求？？？

万恶之源 \\(\\Rightarrow [l,r] \\huge{[l,r]}\\)

然后，事情就变得不简单了。。。

---

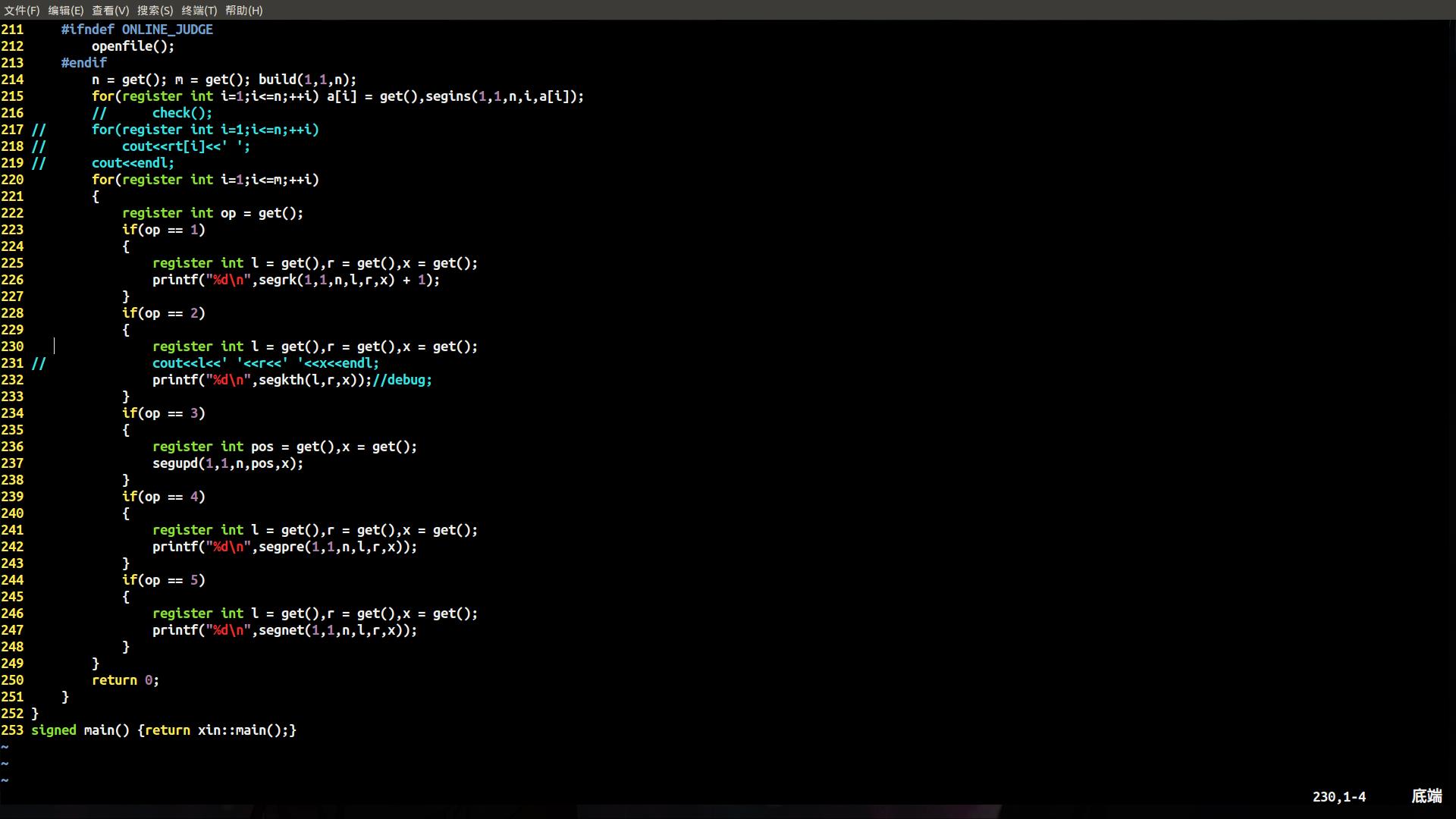
不就是个 \\(250\\) 行呗。。。

不就是个线段树上每一个区间节点上套一个 \\(splay\\;tree\\) 呗。。。

不就是死活调不对呗。。。

不就是输出一堆 \\(2147483647\\) 呗。。。

不就是。。。。

---

当我精神几近崩溃的时候，\\(zxb\\) 出现，他是来拯救我的。。。

用双指针

。。。。

---

将其赶走之后，在历经下午，晚上，早读，上午将近 \\(6\\) 小时的努力下，终于。。。。

不 \\(RE\\) 了

（此处省略 \\(10000\\) 字，请自行脑补）

---

但最后凭借坚强的毅力 f**k调试法,终于调出了样例，本以为会 然而却， \\(\\huge{\\text{心中狂喜}}\\)

然鹅连luogu最差解都算不上

主要做法就是对于整个序列建造一颗线段树，用来划分区间。

之后对于整个序列进行一个建树操作，就可以建造出每一个可行序列。

在每个序列当中，并不需要有什么权值。

只需要一个 \\(root\\) 来维护 \\(splay\\;tree\\) 的根。

这样每一个 \\(splay\\;tree\\) 就可以划分清楚，互不干扰。

建树的时候在每个点再建造一棵 \\(splay\\;tree\\) 用来维护那要求的 \\(5\\) 个操作，记得还要 \\(insert\\) 一个 \\(2147483647\\) 防止找不到 \\(pre\\) 和 \\(next\\)

之后的 \\(kth\\) \\(rank\\) \\(rotatr\\) \\(splay\\) \\(search\\) \\(pre\\) \\(next\\) \\(del\\) 操作就大同小异了，其实就是在需要使用根节点的函数多传一个 \\(node\\) 参数用来区分。

然后线段树操作也就是 \\(segins\\) \\(segkth\\) \\(segrk\\) \\(segpre\\) \\(segnext\\) \\(build\\)

也就是将近20个函数，一点都不多。。。

真 不多

---

然后就可以开始漫长的 \\(debug\\) 过程了，这才是全部的 \\(90%\\) 才对。。。

当你这道题目调试完看到时，比做出任何一道题都有成就感。。。

所以来 \\(k\\) \\(k\\) 我的小代码ba。。。。

#include<bits/stdc++.h>
using namespace std;
//#define int long long
#define debug cout<<"debug"<<endl
#define freopen eat2 = freopen
#define scanf eat1 = scanf
#define INF 2147483647
#define inf INF
#define cao cout<<endl
namespace xin_io
{
	#define gc() p1 == p2 and (p2 = (p1 = buf) + fread(buf,1,1<<20,stdin),p1 == p2) ? EOF : *p1++
	#define scanf eat1 = scanf 
	#define freopen eat2 = freopen
	char buf[1<<20],*p1 = buf,*p2 = buf;FILE *eat2;
	inline void openfile() {freopen("t.txt","r",stdin);} inline void outfile(){freopen("o.txt","w",stdout);}
	inline int get()
	{
		int s = 0,f = 1;register char ch = gc();
		while(!isdigit(ch))
		{if(ch == \'-\') f = -1;ch = gc();}
		while(isdigit(ch))
		{s = s * 10 + ch - \'0\';ch = gc();}return s * f;
	}
}
using namespace xin_io; int eat1;
static const int maxn = 1e6+10,mod = 1e6;
inline int min(int x,int y) {return x > y ? y : x;} inline int max(int x,int y) {return x > y ? x : y;}
#define ls(x) t[x].son[0]
#define rs(x) t[x].son[1]
namespace xin
{
	#define pushup(x) t[x].size = t[ls(x)].size + t[rs(x)].size + t[x].tot
	class xin_splay{public:int size, tot, val,son[2],fa;}t[maxn * 50];
	int rt[maxn];
	int a[maxn], n, m, cnt;
	inline void rotate(int x)
	{
		register int y = t[x].fa,z = t[y].fa;
		register int ki = t[y].son[1] == x;
		t[z].son[t[z].son[1] == y] = x; t[x].fa = z;
		t[y].son[ki] = t[x].son[ki xor 1]; t[t[x].son[ki xor 1]].fa = y;
		t[x].son[ki xor 1] = y; t[y].fa = x;
		pushup(y); pushup(x);
	}
	inline void splay( int x, int goal, int node ) 
	{
		while( t[x].fa != goal ) 
		{
			int y = t[x].fa,z = t[y].fa;
			if(z != goal) (t[z].son[1] == y) ^ (t[y].son[1] == x) ? rotate(x) : rotate(y);
			rotate(x); 
		}
		if(!goal) rt[node] = x;
	}
	inline int init( int v, int fa ) {t[++cnt].val = v, t[cnt].fa = fa, t[cnt].tot = 1;pushup(cnt); return cnt;}
	inline void insert( int x, int node ) 
	{
		int u = rt[node],fa = 0;
		if(!u) { u = init(x, 0), rt[node] = u; return ;}
		while(u and t[u].val != x) fa = u, u = t[u].son[t[u].val < x];
		if(u) t[u].tot ++;
		else
		{	
			u = init(x, fa);
			if(fa) t[fa].son[t[fa].val < x] = u;
		}
		splay(u,0,node ); 
	}
	inline void search( int x, int node) 
	{
		int u = rt[node];  if(!u) return ;
		while( t[u].son[t[u].val < x] and t[u].val != x) 
			u = t[u].son[t[u].val < x];
		splay( u, 0, node );
	}
	inline int next( int x, int typ, int node )
	{
		search(x, node); int u = rt[node];
		if((typ and t[u].val < x) || (!typ and t[u].val > x)) return u;
		u = t[u].son[typ ^ 1];
		while(t[u].son[typ]) u = t[u].son[typ];
		return u;
	}
	inline void del( int x, int node) 
	{
		int u = rt[node], pre = next(x, 1, node), nxt = next(x,0,node);
		splay(nxt, 0, node); splay(pre, nxt, node);
		int pos = t[pre].son[1];
		if(t[pos].tot > 1) -- t[pos].tot, splay(pos, 0, node);
		else t[pre].son[1] = 0;
		pushup(pre); 
	}
	inline void build(int node,int l,int r)
	{
		insert(inf,node); insert(-inf,node);
		if(l == r) return;
		register int mid = (l + r) >> 1;
		build(node<<1,l,mid); build(node << 1| 1,mid+1,r);
	}
	inline void segins(int node,int l,int r,int k,int val)
	{
		register int mid = (l + r) >> 1;
		insert(val,node);if(l == r) return ;
		if(mid >= k) segins(node << 1,l,mid,k,val);
		else segins(node << 1| 1,mid+1,r,k,val);
	}
	inline int segrk(int node,int l,int r,int k,int ql,int qr)
	{
		if(qr < l or ql > r) return 0;
		if(ql <= l and qr >= r) 
		{
			search(k,node); register int u = rt[node];
			if(t[u].val >= k) return t[ls(u)].size - 1;
			else return t[ls(u)].size + t[u].tot - 1;
		}
//		cout<<node<<\' \'<<l<<\' \'<<r<<endl;
		register int mid = (l + r) >> 1;
		return segrk(node << 1,l,mid,k,ql,qr) + segrk(node << 1| 1,mid+1,r,k,ql,qr);
	}
	inline void segupd(int node,int l,int r,int pos,int val)
	{
		del(a[pos],node); insert(val,node);
		if(l == r and r == pos) {a[pos] = val;return ;}
		register int mid = (l + r ) >> 1;
		if(mid >= pos) segupd(node << 1,l,mid,pos,val);
		else segupd(node << 1| 1,mid+1,r,pos,val);
	}
	inline int segnxt(int node,int l,int r,int ql,int qr,int k)
	{
		if(l > qr or r < ql) return inf;
		if(l >= ql and r <= qr) return t[next(k,0,node)].val;
		register int  mid = (l + r )>> 1;
		return min(segnxt(node << 1,l,mid,ql,qr,k) , segnxt(node << 1 | 1,mid + 1,r,ql,qr,k));
	}
	inline int segpre(int node,int l,int r,int ql,int qr,int k)
	{
		if(l > qr or r < ql) return -inf;
		if(l >= ql and r <= qr) return t[next(k,1,node)].val;
		register int mid = (l + r) >> 1;
		return max(segpre(node << 1,l,mid,ql,qr,k) , segpre(node << 1| 1,mid+1,r,ql,qr,k));
	}
	inline int segkth(int ql,int qr,int k)
	{
		register int l = 0,r = 1e8,ret;
		while(l <= r)
		{
			register int mid = (l + r) >> 1;
			register int judge = segrk(1,1,n,mid,ql,qr) + 1;
			if(judge > k) r = mid - 1;
			else l = mid + 1, ret = mid;
		}
		return ret;
	}
	inline void check()
	{
		for(register int i=1;i<=cnt;++i)
			cout<<"i = "<<i<<" t[i].val = "<<t[i].val<<" t[i].size = "<<t[i].size<<endl;
		cout<<endl;
	}
	inline short main()
	{
	#ifndef ONLINE_JUDGE
		openfile();
	#endif
		n = get(); m = get(); build(1,1,n);
//		check();
		for(register int i=1;i<=n;++i) a[i] = get(),segins(1,1,n,i,a[i]);
//		check();
		for(register int i=1;i<=m;++i)
		{
			register int op = get();
			if(op == 1)
			{
				register int l = get(),r = get(),x = get();
				printf("%d\\n",segrk(1,1,n,x,l,r) + 1);
			}
			if(op == 2)
			{
				register int l = get(),r = get(),k = get();
				printf("%d\\n",segkth(l,r,k));
			}
			if(op == 3)
			{
				register int pos = get(),x = get();
				segupd(1,1,n,pos,x);
			}
			if(op == 4)
			{
				register int l = get(),r = get(),x = get();
				printf("%d\\n",segpre(1,1,n,l,r,x));
			}
			if(op == 5)
			{
				register int l = get(),r = get(),x = get();
				printf("%d\\n",segnxt(1,1,n,l,r,x));
			}	
		}
		return 0;
	}
}
signed main() {return xin::main();}

\\(\\huge{\\color{red}{\\text{真好玩}}}\\)