分治策略

Posted 2021-06-13 天亮yǐ后

递归与分治策略

递归的概念

• 一个直接或间接地调用自身的算法成为递归算法。
• 在计算机算法设计与分析中，使用递归技术往往使函数的定义和算法的描述简洁且易于理解。有些数据如二叉树等，由于本身固有的递归特性，特别适合用递归的形式来描述
• 还有一些问题，虽然自身没有明显的递归结构，但用递归技术来求解设计的算法简洁易懂且易于分析

例1：阶乘函数

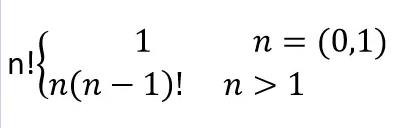
例2：斐波那契数列

例3：双递归函数——Ackerman函数

• 当一个函数及它的一个参数是函数自身定义时，称这个函数为双递归函数

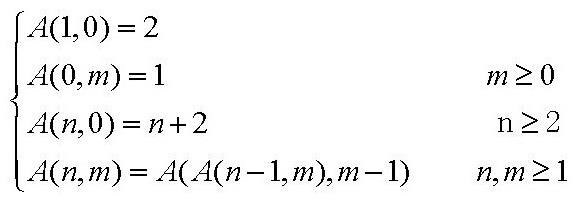
分治法的基本思想

分治法的基本思想是将一个规模为n的问题分解为k个规模较小的子问题，这些子问题相互独立且与原问题相同。递归的解这些子问题，然后将各个子问题的解合并得到原问题的解。

Divide-and-Conquer(P){
    if(|P|<=n0) Adhoc(P);
    divide P into smaller subinstances
    P1,P2,...,Pk;
    for(i=1;i<=k;i++)
        yi=Divide-and-Conquer(Pi);
    return Merge(y1,...,yk);
}

• 其中|p|表示问题P的规模，n0为一阈值，表示当问题P的规模不超过n0时，问题易于解决，不必再继续分解。Adhoc(P)是该分治法的基本子算法，用于直接解出小规模的问题P。因此，当P的规模不超过n0时，直接用Adhoc(P)求解。算法Merge(y1,y2...,yk)是该分治法中的合并子算法，用于将P的子问题P1,P2,...,Pk的解y1,y2,...,yk合并为P的解

例1：二分搜索技术

• 基本思想：将n个元素分成大致相同的两半，去a[n/2]与x做比较。如果x=a[n/2]，则找到x,算法结束。如果x<a[n/2]，则只要在数组a的左半部分继续搜索x。如果x>a[n/2]，则只要在数组a的右半部分继续搜索x。

例2：Strassen矩阵乘法

例3：棋盘覆盖

例4：合并排序

• 基本思想：对n个元素排序，当n=1时，终止排序，否则将待排序元素分成大小大致相同的两个子集合，分别对两个子集合进行排序，最终将排序好的子集合合并成为所需求的排序好的集合。

例5：快速排序

• 基本思想：对输入的子数组a[p:r]，按以下三个步骤进行排序：

1. 分解：以a[q]为基准元素将a[p:r]分为3段，a[p:q-1]，a[q]和a[q+1:r]，使得a[p:q-1]中任何一个元素小于等于a[q]，a[q+1:r]中任何一个元素大于等于a[q]。下标q在划分过程中确定
2. 递归求解：通过递归调用快速排序算法分别对a[p:q-1]和q[q+1:r]进行排序
3. 合并：由于对a[p:q-1]和a[p+1:r]的排序是就地进行的，所以在a[p:q-1]和a[q+1:r]都己排好的序后不需要执行任何计算a[p:r]就已经排好序