使用查找表的经典题

Posted 2021-06-12 程序员小熊

关注公众号【程序员小熊】，后台回复【算法】、【python】、【C++】和【1024】，即可获取海量学习资料。

前言

大家好，我是来自「华为」的「程序员小熊」。清明假期到了，小熊给大家带来一道简单题，让大家放松放松。这道题也是各大厂的面试题，例如苹果、脸书、亚马逊和微软等等。

本文主要介绍通过「查找表」的策略来解答此题，同时也会介绍「双指针」中的「对撞指针」方法，供大家参考，希望对大家有所帮助。

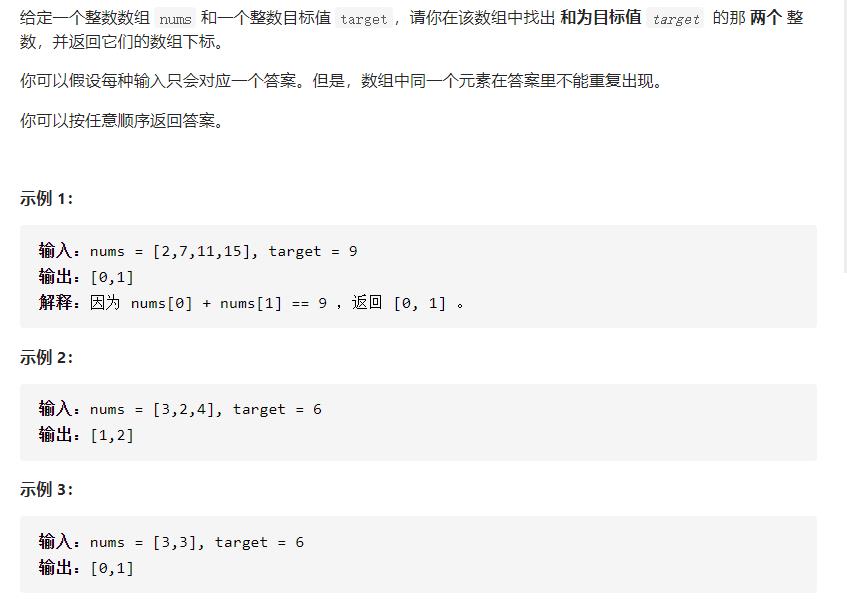
两数之和

 

 

 

 

解题思路

在数组（「不一定有序」）中查找两个元素，使得「其和等于目标值」，求这两个元素的下标。最容易想到的方法是「暴力法」，只需要「枚举」数组中所有的不同的两个元素组合，判断其和是否等于目标值 target 即可。

暴力法

两层遍历数组，找出数组中不同的两个下标，使其对应的元素之和等于目标值 target。

Show me the Code

「C」

 1 int* twoSum(int* nums, int numsSize, int target, int* returnSize){
 2     *returnSize = 0;
 3     int *res = (int *)malloc(sizeof(int) * 2);
 4     if (res == NULL) {
 5         return NULL;
 6     }
 7 
 8     
 9     for(int i = 0; i < numsSize - 1; ++i) {
10         for(int j = i + 1; j < numsSize; ++j) {
11             if(nums[i] + nums [j] == target) {
12                 res[0] = i;
13                 res[1] = j;
14                 *returnSize = 2;
15                 return res;
16             }
17         }       
18     }
19     
20     return NULL;      
21 }

View Code

「复杂度分析」

时间复杂度：「O(n^2)」，其中 n 是数组的长度，两层遍历数组。

空间复杂度：「O(1)」，未开辟额外的空间。

哈希表

如果在面试中，只提供「暴力法」的解题思路，面试官往往「不太满意」，会问候选人还有没有「更优的」解题方法；而且本题「进阶」中也提示能否想出一个时间复杂度低于「O(n^2)」 的算法。

可以考虑采用「空间换时间」的策略，来降低时间复杂度。假设待查找的一个元素是 a，则另一个待查找的元素为 target - a，因此在遍历数组时，可以通过「记录 a 和其下标」，并判断「target - a 是否在记录的查找表中」，从而将时间复杂度降到「O(n)」。

「举例」

以数组 nums = [2,7,11,15]，target = 9 为例子，采用「哈希表」的策略，其查找过程如下动图示。

Show me the Code

「C++」

 1 vector<int> twoSum(vector<int>& nums, int target) {
 2     unordered_map<int, int> record;
 3     for (int i = 0; i < nums.size(); ++i) {
 4         int theOther = target - nums[i];
 5         if (record.find(theOther) != record.end()) {
 6             int res[2] = {i, record[theOther]};
 7             return vector<int>(res, res + 2);
 8         }
 9         record[nums[i]] = i;
10     }
11 
12     return {};
13 }

View Code

「java」

 1 int[] twoSum(int[] nums, int target) {
 2     int len = nums.length;
 3     Map<Integer, Integer> record = new HashMap<Integer, Integer>();
 4     for (int i = 0; i < nums.length; ++i) {
 5         int theOther = target - nums[i];
 6         if (record.containsKey(theOther)) {
 7             return new int[]{record.get(theOther), i};
 8         }
 9         record.put(nums[i], i);
10     }
11     
12     return new int[0];     
13 }

View Code

「Python3」

1 def twoSum(self, nums: List[int], target: int) -> List[int]:
2     hashtable = dict()
3     for i, num in enumerate(nums):
4         theOther = target - num
5         if theOther in hashtable:
6             return [hashtable[theOther], i]
7         hashtable[nums[i]] = i
8     return []

View Code

「复杂度分析」

时间复杂度：「O(n)」，其中 n 是数组的长度。在哈希表中查找 target - a 只需要「O(1)」 的时间复杂度。

空间复杂度：「O(n)」，其中 n 是数组中元素个数。主要用于开辟长度为 n 的哈希表。

双指针

如果数组是「有序」的话，了解「双指针」的童鞋，很容易想到可以通过双指针中的「对撞指针」的方法去求解，由于题目没有告知数组是有序的，所以要想使用「对撞指针」，首先得对数组进行「排序」。

排序完成之后，初始化两个指针，其中首指针指向数组第一个元素，尾指针指向数组的最后一个元素，然后判断其指向的「元素之和是否等于目标值」，如果等于，则直接返回两下标，否则「移动首尾指针」（小于目标值，右移首指针；否则，左移尾指针），直至找到。

Show me the Code

「C」

 1 int cmp(const void *a, const void *b) {
 2     return *(int *)a - *(int *)b;
 3 }
 4 
 5 /* 对撞指针获取数组中元素之和等于 target 的两元素 */
 6 void getIdxOfNumsByTwoPoints(int *arr, int arrSize, int target, int *l, int *r) {
 7     int left = 0, right = arrSize - 1;
 8     while (left <= right) {
 9         int value = arr[left] + arr[right];
10         if (value < target) {
11             left++;
12         } else if (value > target) {
13             right--;
14         } else {
15             *l = left;
16             *r = right;
17             break;
18         }
19     } 
20     
21     return;   
22 }
23 
24 /* 获取第一个元素的下标 */
25 int obtainIdxFromArr(int *arr, int arrSize, int target) {
26     for (int i = 0; i < arrSize; ++i) {
27         if (arr[i] == target) {
28             return i;
29         }
30     }
31 
32     return -1;    
33 }
34 
35 /* 获取第二个元素的下标 */
36 int obtainIdxFromArrNotRepeat(int *arr, int arrSize, int target, int k) {
37     for (int i = 0; i < arrSize; ++i) {
38         if (arr[i] == target && i != k) {
39             return i;
40         }
41     }
42 
43     return -1;    
44 }
45 
46 int* twoSum(int* nums, int numsSize, int target, int* returnSize){
47     *returnSize = 0;
48     int *arr = (int *)malloc(numsSize * sizeof(int));
49     if (arr == NULL) {
50         return NULL;
51     }
52 
53     /* 拷贝一份 nums 用于排序查找 */
54     memcpy(arr, nums, numsSize * sizeof(int));
55     qsort(arr, numsSize, sizeof(int), cmp); 
56 
57     int ret = 0;
58     int one = 0, theOther = 0;
59     getIdxOfNumsByTwoPoints(arr, numsSize, target, &one, &theOther);
60 
61     int *res = (int *)malloc(2 * sizeof(int));
62     if (res == NULL) {
63         return NULL;
64     }
65     
66     memset(res, -1, sizeof(int) * 2);    
67     res[0] = obtainIdxFromArr(nums, numsSize, arr[one]);
68     if (res[0] == -1) {
69         return NULL;
70     }
71 
72     res[1] = obtainIdxFromArrNotRepeat(nums, numsSize, arr[theOther], res[0]);
73     if (res[1] == -1) {
74         return NULL;
75     }
76 
77     *returnSize = 2;
78     return res;
79 }

View Code

 

「复杂度分析」

时间复杂度：「O(nlogn)」，其中 n 是数组的长度。遍历数组「O(n)」，快排「O(nlogn)」，两者之和还是「O(nlogn)」。

空间复杂度：「O(n)」，其中 n 是数组的长度，开辟了额外空间，用于排序。

 

更多精彩

关注公众号「程序员小熊」