dp-数字三角形

Posted 2021-06-12 Lee先森的博客

数字三角形问题是一个很经典的dp问题，因为这个题是在书上看到的，所以根本不知道输入是什么！只能通过经验判断输入！！！！

注意：当前版本是我自己臆想出来的输入。

题目描述

有一个非负整数组成的三角形，第一行只有一个数，除了最下行之外每个数的左下方和右下方各有一个数，从第一行的数开始每次可以往左下或者右下走一格，直到走到最下行，把沿途经过的数全部加起来，如何走才能得到最大和？

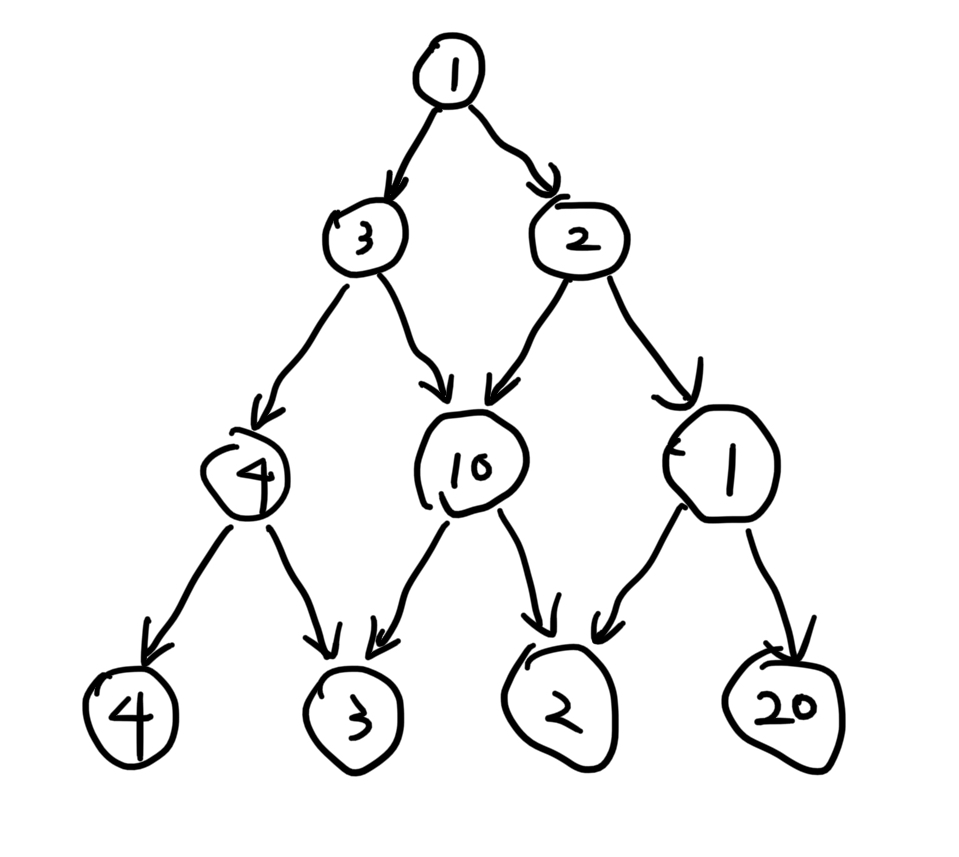
思考过程1

像题目中这样说，不就是转换成一个数组么？

如图所示，先转成数组：

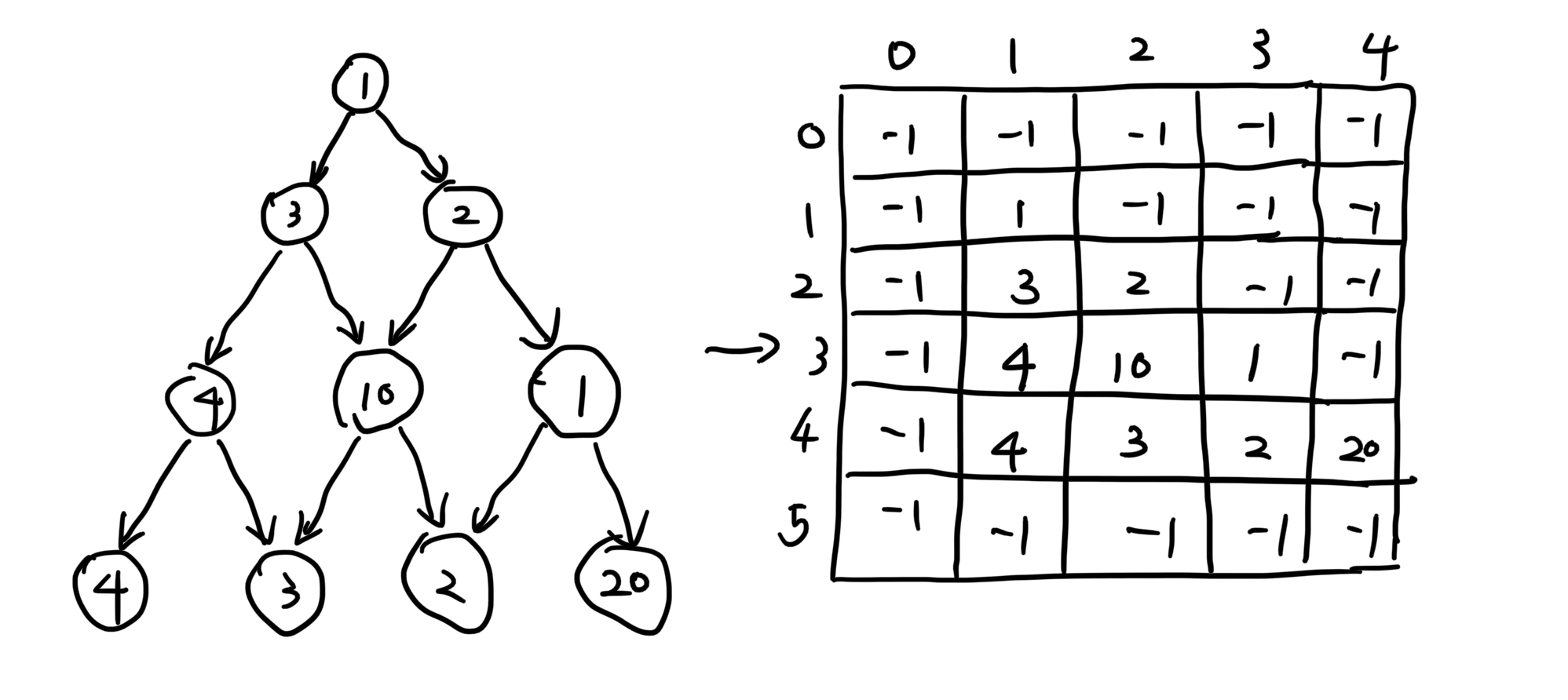
注意：第\\(0\\)行和第\\(0\\)列是不需要的，因为不好计算。第\\(k\\)行有\\(k\\)个数。

像这种结构找最大或者最小值，一般就是用深搜，每条路径都要遍历一遍。确定了深搜之后，想一下输入的问题，我以为这道题的输入是给定\\(n\\)，输入这\\(n\\)个数。所以现在要解决的问题是\\(n\\)个数一共是多少层：假设\\(n\\)个数一共可以组成\\(k\\)层（假设是满的），第\\(1\\)层有\\(1\\)数...第\\(k\\)层有\\(k\\)个数，则一定有：

\\[1 + 2 + 3 + ...+k \\geq n \\]

左边就是个等差数列，结果为：

\\[\\frac{(1+k)*k}{2} \\]

展开可得：

\\[k^2+k-2n \\geq 0 \\]

这里求解\\(k\\)，根据韦达定理，可知：

\\[x=\\frac{-b\\pm \\sqrt{b^2-4ac}}{2a} \\]

同过这个公式可以求得\\(k\\)：

\\[k_1\\geq\\frac{\\sqrt{1+8n}-1}{2} \\\\ k_2\\leq\\frac{-1 - \\sqrt{1+8n}}{2} \\]

因为\\(k_2\\)一定是小于\\(0\\)的，所以\\(k_1\\)为最终答案，但此时一定是满的，需要求解的层数进行上取整ceil()。

深搜代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <vector>
#include <map>
#include <cmath>
#include <deque>

using namespace std;

#define MAX_N 100
#define print(a) { \\
    for (int i = 0; i < 10; i++) {\\
        for (int j = 0; j < 10; j++) {\\
            cout << grid[i][j] << " ";\\
        }\\
        cout << endl;\\
    }\\
}
int n, grid[MAX_N + 5][MAX_N + 5], ans = 0;
int k;

void dfs(int x, int y, int sum) {
    sum += grid[x][y];
    // cout << "(" << x << ", " << y << ")" << " " << sum << endl;
    if (x == k) {
        ans = max(sum, ans);
        return ;
    }
    if (grid[x + 1][y] >= 0) {
        dfs(x + 1, y, sum);
    }
    if (grid[x + 1][y + 1] >= 0) {
        dfs(x + 1, y + 1, sum);
    }
}

void solve() {
    memset(grid, -1, sizeof(grid));
    cin >> n;
    k = ceil((sqrt(1 + 8 * n) - 1) / 2);
    cout << "k = " << k << endl;
    for (int i = 1; i <= k; i++) {
        for (int j = 1; j <= i; j++) {
            cin >> grid[i][j];
            // print(grid);
        }
    }
    dfs(1, 1, 0);
    cout << ans << endl;
}

int main() {
    solve();
    return 0;
}

未完！等回来再写！