在模仿中精进数据分析与可视化01——颗粒物浓度时空变化趋势（Mann–Kendall Test）

Posted 2021-06-11 江流石

简介

  本次要模仿的作品来自论文Investigating the Impacts of Urbanization on PM_2.5 Pollution in the Yangtze River Delta of China: A Spatial Panel Data Approach，研究区域为上海、安徽、浙江和江苏，所用数据为 2002–2017该区域PM_2.5浓度栅格数据，数据来源于 Dalhousie University Atmospheric Composition Analysis Group开发的年均PM_2.5数据集V4.CH.03，空间分辨率为0.01°×0.1°（原论文采用数据的空间分辨率为1km×1km，但我在该网站上找不到，可能是不提供下载了）。

数据下载和处理

数据下载格式为.asc，使用arcpy将其转为.tif格式，所用代码如下。

# -*- coding: utf-8 -*-

import arcpy
import os

inpath = "./ASCII" #待转换的栅格的存储路径，会转换该路径下的所有栅格
outpath = "./TIF" #输出栅格的路径，最好是空路径
filetype = "FLOAT"

print "Starting Convert!"
for filename in os.listdir(inpath):
    if filename.endswith(".asc"):
        filepath = os.path.join(inpath, filename)
        outfilepath = os.path.join(outpath, filename.replace(".asc", ".tif"))
        arcpy.ASCIIToRaster_conversion(filepath, outfilepath, filetype)
print "Convert Over!"

Mann–Kendall趋势分析

  Mann–Kendall趋势分析的具体计算方法这里不再赘述，原文作者采用R语言的trend package计算的，本文采用python的pymannkendall计算，github项目地址为https://github.com/mmhs013/pyMannKendall。
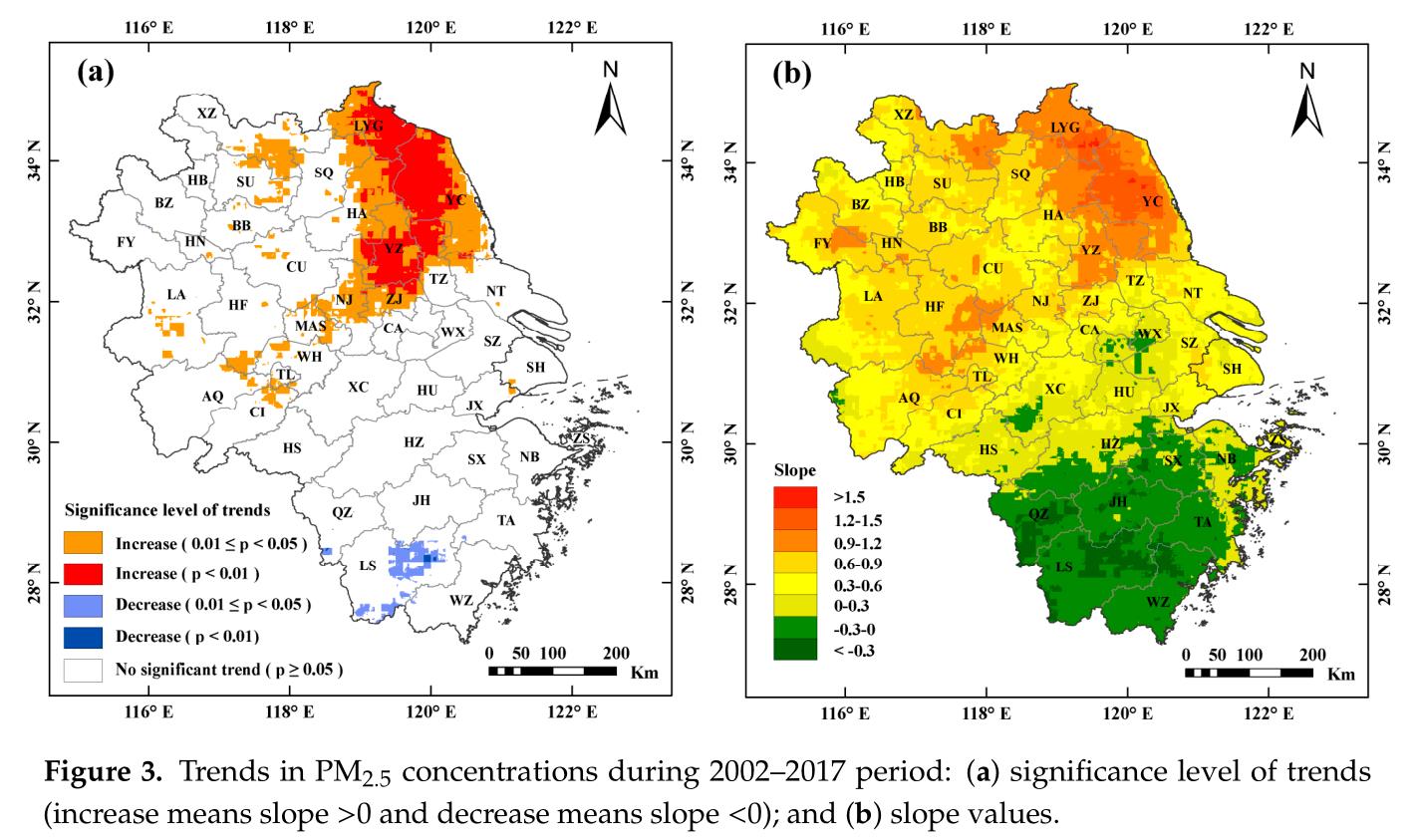
  原文的趋势分析包括两部分，一部分是计算slope值，slope值越大，则表明上升的趋势越明显，反之亦然；另一部分是计算p值，p值越小趋势越显著，0.01<p<0.05说明趋势显著，p<0.01说明趋势非常显著。二者分别采用pymannkendall的sens_slope和original_test函数计算，\'pymannkendall\'的简单用法介绍如下。

A quick example of pyMannKendall usage is given below. Several more examples are provided here.

import numpy as np
import pymannkendall as mk

# Data generation for analysis
data = np.random.rand(360,1)

result = mk.original_test(data)
print(result)

Output are like this:

Mann_Kendall_Test(trend=\'no trend\', h=False, p=0.9507221701045581, z=0.06179991635055463, Tau=0.0021974620860414733, s=142.0, var_s=5205500.0, slope=1.0353584906597959e-05, intercept=0.5232692553379981)

Whereas, the output is a named tuple, so you can call by name for specific result:

print(result.slope)

or, you can directly unpack your results like this:

trend, h, p, z, Tau, s, var_s, slope, intercept = mk.original_test(data)

计算并保存结果

  这里依然使用arcpy作为分析计算的工具，所用代码如下，pymannkendall较为臃肿，计算速度很慢(我用了十几分钟)，并且暂不支持numba加速，有需要大量计算的可根据其源码从新编写函数，实现numba加速，如本文的get_slope函数。

# -*- coding: utf-8 -*-

import arcpy
import os
from glob import glob
import numpy as np
import pymannkendall as mk

inpath = r"./TIF" #.tif文件的保存路径
p_path = r"./pvalues.tif" #p-values的输出路径
slope_path = r"./slopes.tif" #slopes的输出路径
trend_path = r"./trends.tif"
border_path = r"./Shapefiles/border.shp" #研究区域

# 获取2002-2017年的栅格数据的路径
def get_raster_paths(inpath):
    paths = []
    for year in range(2002, 2018):
        year_path = glob(os.path.join(inpath, "*"+str(year)+"*.tif"))
        if year_path:
            paths.append(year_path[0])
        else:
            print "can\'t find raster of {} year!".format(year)
    return paths

# 裁剪栅格，并将结果转为numpy数组
def clip_raster_to_array(paths, border):
    out_image = arcpy.sa.ExtractByMask(paths[0], border)
    # 掩膜提取
    x_cell_size, y_cell_size = out_image.meanCellWidth, out_image.meanCellHeight #x,y方向的像元大小
    ExtentXmin, ExtentYmin = out_image.extent.XMin, out_image.extent.YMin #取x,y坐标最小值
    lowerLeft = arcpy.Point(ExtentXmin, ExtentYmin ) #取得数据起始点范围
    noDataValue = out_image.noDataValue #取得数据的noData值
    out_image = arcpy.RasterToNumPyArray(out_image) #将栅格转为numpy数组
    out_image[out_image==noDataValue] = np.NAN #将数组中的noData值设为nan
    arrays = np.full(shape=(len(paths), out_image.shape[0], out_image.shape[1]),
                     fill_value=np.NAN, dtype=out_image.dtype)
    arrays[0] = out_image
    
    for i in range(1, len(paths)):
        out_image = arcpy.sa.ExtractByMask(paths[i], border)
        arcpy.SetRasterProperties_management(out_image, \'#\', \'#\', \'#\', "1 {}".format(noDataValue))
        out_image = arcpy.RasterToNumPyArray(out_image)
        out_image[out_image==noDataValue] = np.NAN
        arrays[i] = out_image
    
    return arrays, (lowerLeft, x_cell_size, y_cell_size, noDataValue)

def array_to_raster(path, data, rasterInfo):
    new_raster = arcpy.NumPyArrayToRaster(data, *rasterInfo) #数组转栅格
    new_raster.save(path) #保存栅格

# 计算slope值
def get_slope(x):
    if np.isnan(x).any():
        return np.NAN
    idx = 0
    n = len(x)
    d = np.ones(int(n*(n-1)/2))

    for i in range(n-1):
        j = np.arange(i+1,n)
        d[idx : idx + len(j)] = (x[j] - x[i]) / (j - i)
        idx = idx + len(j)
        
    return np.median(d)

# 计算p值
def get_pvalue(x):
    if np.isnan(x).any():
        return np.NAN
    result = mk.original_test(x)
    return result.p

paths = get_raster_paths(inpath)
arrays, rasterinfo = clip_raster_to_array(paths, border_path)
print "clip raster to array over!"

slopes = np.apply_along_axis(get_slope, 0, arrays)
print "calculate p-value over!"
pvalues = np.apply_along_axis(get_pvalue, 0, arrays)
print "calculate slope over!"

#计算有显著和比较显著趋势的区域
trends = np.full(shape=slopes.shape, fill_value=np.NaN)
trends[~np.isnan(slopes)] = 0 #不显著的区域设为0
trends[(slopes>0) & ((0.01<pvalues) & (pvalues<0.05))] = 1 #比较显著增加的区域设为1
trends[(slopes>0) & (pvalues<0.01)] = 2 #显著增加的区域设为2
trends[(slopes<0) & ((0.01<pvalues) & (pvalues<0.05))] = 3 #比较显著减少的区域设为3
trends[(slopes<0) & (pvalues<0.01)] = 4 #显著减少的区域设为4

# 保存栅格
array_to_raster(p_path, pvalues, rasterinfo)
array_to_raster(slope_path, slopes, rasterinfo)
array_to_raster(trend_path, trends, rasterinfo)
print "save rasters over!"

结果绘图