单纯形法剖析，一句话描述单纯形法

Posted 2021-06-10 雾恋过往

一句话描述单纯形法：

从可行域的一个顶点跳到另一个顶点，使得目标函数改善的过程。直到满足终止条件。

解释一下这句话

可行域的顶点？其实就是所谓的基可行解

终止条件，其实就是所谓的检验数全为非正。

这儿得注意，检验数有为0的意味着可能存在无穷多个最优解，即在两个顶点连线上的点都是最优，还有一个就是无有限解，解无穷大，这个的判断是在进基时发现这个基对应的约束系数（这儿的系数是我们变换了的，不是最开始的啊）全是负的

问题来了？

1、第一个顶点（基可行解）怎么产生？

答：有的问题可以直接看出约束的系数矩阵里面有单位阵，有的则不好看出来或者看不出来。那么用大M法，或者两阶段法产生一个基可行解，如果产生不了，说明无解。

这个大M法和两阶段法自己去看。

2、你说从一个顶点跳到另一个顶点？怎么跳？

答：这就是所谓的进基的出基，目的是从一个基可行解得到另一个基可行解。

3、进基与出基，我该进那个出那个呢？

答：进基一般进检验数最大的那个（也有按顺序对检验数大于0的进基），出基其实不是你决定的，它决定于你进基的是那个，因为我们进基肯定把这个基最大的来进，举个列子

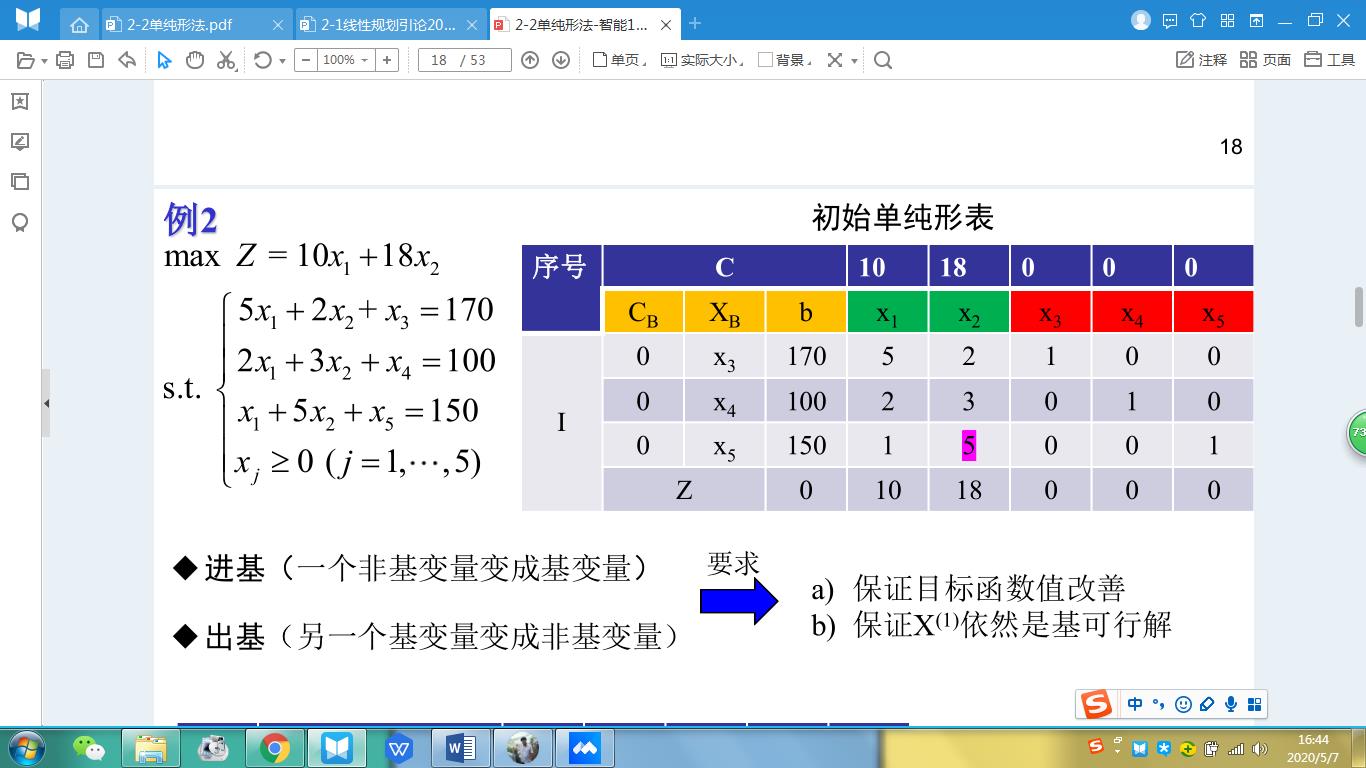
这张图最开始的基是x{3,4,5}，我们进基，18>10，所以我们肯定是进x2。进多少呢？
第一个约束最大允许我们进85，第二个100/3，第三个30.显然我们要满足所有约束，那么就是进30，自然而然，出基的就是第三个约束中的x5。所以说你进基的元素决定了你出基的元素

过程如下

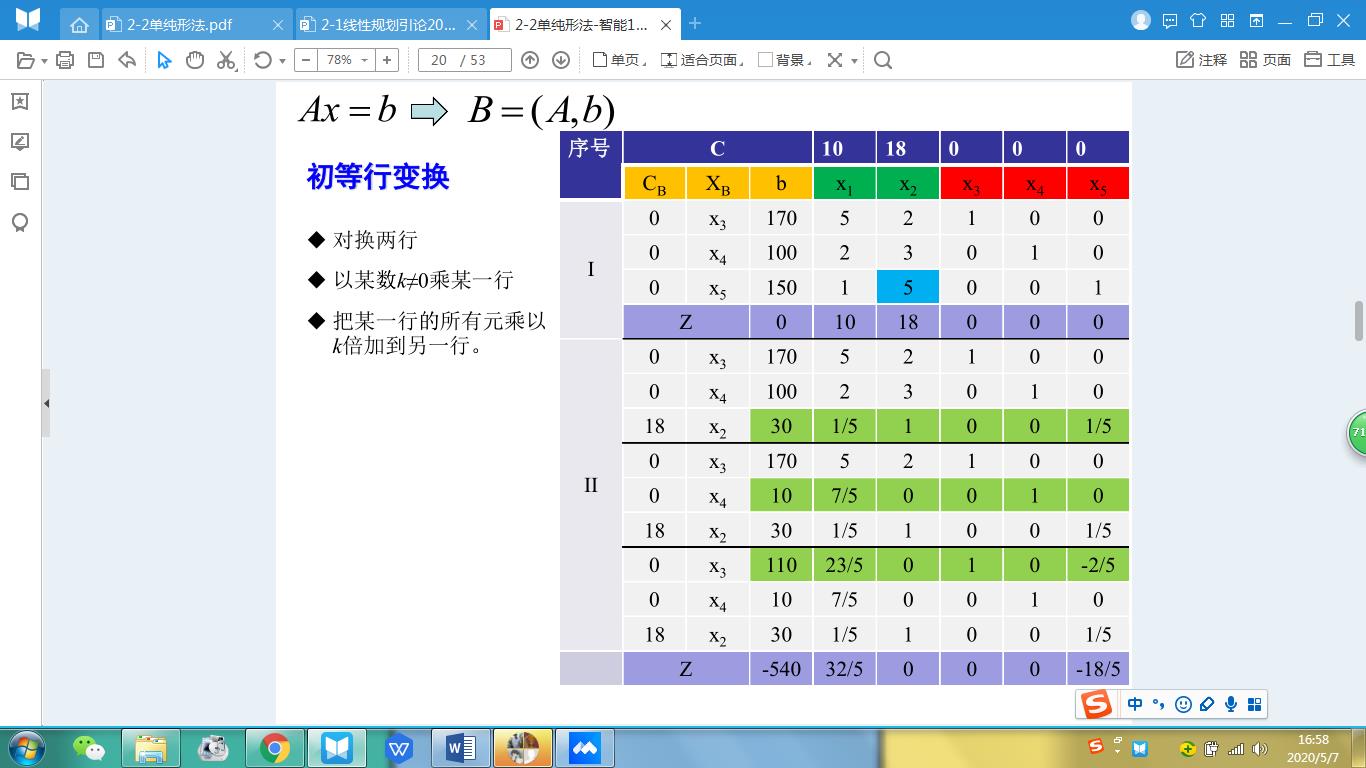
4、好的，现在我进基完了，也用非基变量表示我的目标函数了，我接下来是继续进基呢，还是停止？

答：看是否满足终止条件 1、所有的检验数为负吗? 是的，那么恭喜，找到了最优解。
2、检验数里面没有正的但是有0？是的，那么说明最优解有无穷多个，即在两个顶点连线上的点都是最优解。上述两个情况都不是，进基。

刚刚第三个问题没说，在进基时要判断进的这个基是不是约束系数都小于0了，全小于0的话说明这个问题没有有限最优解，也就是说最优解无穷大。

也很容易理解啊，如果全为负，我们又是等式约束，我们说了希望进基最大，那么我把这个基进无穷大，负的系数乘以无穷大是无穷小，肯定在我的等式约束内，这样一来我们的基可行解（顶点）的某个坐标不就跑到无穷去了吗，那可不就是没有有限最优解嘛。