带花树笔记

Posted 2021-06-07 chasedeath

带花树笔记

前言：名字的由来

树：增广交替树，即从\\(u\\)开始，由匹配边和增广边交替构成的树

对于二分图，增广过程中忽略偶环，因此就是一棵树

花：一般图存在奇环，在扩展增广树的过程中遇到奇环，就将奇环叫做花

与匈牙利算法的比较

算法的基本框架与匈牙利相同：

依次选取每个点作为根\\(rt\\)，找到一条从根出发的增广路

增广路

是一条从根开始的路径，满足路径由已经确定的匹配边和增广边交替构成

且路径两段的边都是增广边，每个点至多被经过一次

二分图匹配算法的最终目的，都是找到一条增广路

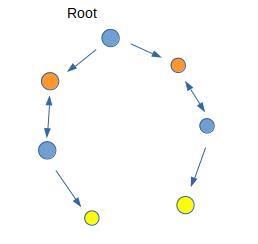
图中双箭头表示匹配边，单箭头表示增广边

按照每个点被遍历的情况进行染色

设\\(col_{rt}=1\\)，即图中的蓝色点，这类节点为 增广节点

另一类点的\\(col_{i}=2\\)，即图中的黄色/橙色节点

匈牙利算法

匈牙利算法采用\\(\\text{dfs/bfs}\\)直接搜索增广路

原因是：确定根之后每个点，每个点的\\(\\text{col}\\)固定，且一定存在一条合法的交替路径

只需要判断是否存在一个\\(col\\)为2的自由节点即可

为什么一般图不行？

\\(\\mathbb{Naive}\\)的想法是：记录每个点是否能作为\\(\\text{1/2}\\)型点

存在的问题：

考虑一般图存在奇环，一个点如果绕奇环回到\\(u\\)，产生不一样的\\(col\\)

而此时路径上就存在点的重复，这就违背了交替路径的性质

正式进入带花树

带花树算法的框架通过广搜建立一棵外向树，不妨称之为增广树

根据上面的分析，其实我们的算法目的是：

确定是否存在一条合法的交替路径，使得一个点\\(col=1,2\\)

为什么采用\\(\\text{bfs}\\)

如果采用\\(\\text{dfs}\\)，产生的边就有：

1.树边

2.返祖边

3.横叉边

4.指向后代的边

\\(\\text{dfs}\\)生成树中，2,3,4类边都可能构成环

如果采用\\(\\text{bfs}\\)，只需要考虑3类边成环

且环的两端一定对应增广树上非祖先关系的两个点

每次从队列中取出节点，试图增广一条边\\((u,v)\\)，几种情况如下

1.\\(v\\)还未被访问过

1-1.\\(v\\)是空点，找到匹配路径

1-2.\\(v\\)已经被匹配，此时满足交替，扩展树形，从其匹配点继续

2.遇到偶环：依然忽略，因为对于增广无益

3.遇到奇环，即\\(col_u=col_v=1\\)

此时，奇环的两端对应树上一段交替的匹配路径

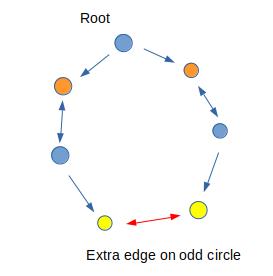
（为了简化情况，仅保留了花所在的部分）

此时，可以发现：

从环的两边分别遍历下来，总能得到一个点\\(col\\)分别为\\(1,2\\)的情况

具体的，考虑最终增广路的样子

容易发现，对于任意合法增广路，总存在等价增广路，且其不经过奇环两次

1.穿过一个1类点（平凡情况）

此时直接翻转原先所在的路径

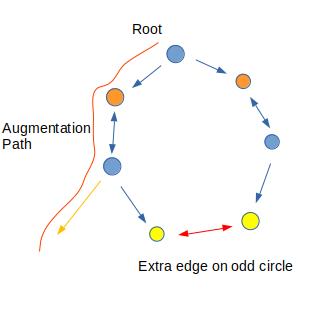
2.穿过2类点：额外情况

此时，通过环的另一边的路径恰好为我们需要的路径

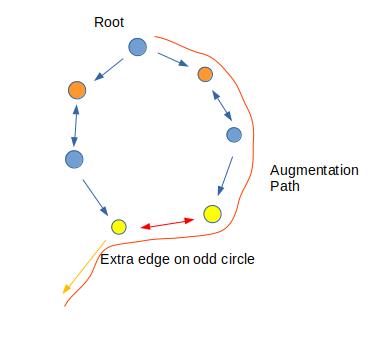
当然，花根不满足这个性质，所以才需要特殊处理

所以操作的结果是：

1.除了花根以外的所有\\(col=2\\)的点，增加\\(col=1\\)的情况

2.除了花根以外的所有\\(col=1\\)的点，增加\\(col=2\\)的情况

由于\\(2\\)型点不主动增广，所以处理奇环实际上就是：将奇环上的每个点视为1型点进行增广

那么我们可以直接将环上的点缩成一个点

同时将每个未被增广的点（即原先\\(col=2\\)）\\(col\\)改为\\(1\\)，加入队列

由于在处理过程中修改了图的结构，需要用并查集维护

实际实现细节较多，突出表现在：

1.在进行合并时，要在在一定程度上保留原路径的形态，以便最终找到增广路径后复原

容易发现，最终的增广路径会在环上走反边，因此原先的增广边需要加入改为双向边

最终的图就变成了

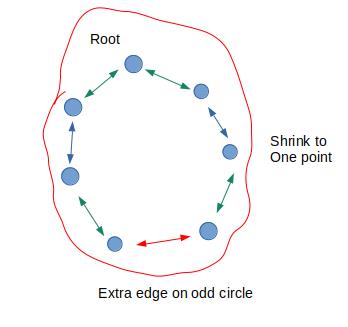
2.实际实现时并不能像合并树链一样每次找深的点跳上去

解决方法：先找到两个点的\\(\\text{LCA}\\)，然后分别合并两段路径

找到\\(\\text{LCA}\\)的过程为保证复杂度：

交替地跳两个节点，直到一个点被遍历了两次，那个点就是\\(\\text{LCA}\\)

这样复杂度就是：较深节点到\\(\\text{LCA}\\)距离\\(\\times 2\\)

遍历标记不方便清空，所以采取时间戳的方式（详见代码）

这样就能做到合并节点复杂度为均摊\\(O(n)\\)（忽略了并查集哈）

总复杂度\\(O(nm)\\)，写不好可能为\\(O(n^3)\\)

const int N=510,INF=1e9+10,P=1e9+7;

int n,m;
vector <int> G[N];
int col[N]; // vertex type
int F[N]; // for union find set 
int match[N]; // match[u]=v ,match[v]=u holds if match[u]!=0
int pre[N]; // previous vertex on alternating tree
int Find(int x){ return F[x]==x?x:F[x]=Find(F[x]); }
// Switch augmentation path
void Switch(int u){
	// match one by one...
	while(u) {
		int t=match[pre[u]];
		match[match[pre[u]]=u]=pre[u];
		u=t;
	}
}

int LCA(int u,int v) {
	static int clo,vis[N];
	clo++;
	// lca method: step by step !!!
	// the problem is : we don\'t know the depths of both vertices
	// but we can keep jumping alternatively , until the deeper vertex reaches lca
	// so the complexity is the distance between deeper vertex and lca
	while(1) {
		if(u) {
			u=Find(u);
			if(vis[u]==clo) return u;
			vis[u]=clo;
			u=pre[match[u]];
		}
		swap(u,v);
	}
}

queue <int> que;
void Shrink(int u,int v,int f) {
	// shrink the path v->u->f
    // add reverse edge 
    // turn point of type1 to type2 ,and push in
	while(Find(u)!=f) {
		pre[u]=v,v=match[u];
		if(col[v]==2) col[v]=1,que.push(v);
		if(Find(u)==u) F[u]=f;
		if(Find(v)==v) F[v]=f;
		u=pre[v];
	}
}

int Bfs(int u) {
	rep(i,1,n) col[i]=pre[i]=0,F[i]=i;
	while(!que.empty()) que.pop();
	que.push(u),col[u]=1;
	//cout<<"tryna match "<<u<<endl;
	while(!que.empty()) {
		int u=que.front(); que.pop();
		assert(col[u]==1);
		for(int v:G[u]) {
			if(Find(u)==Find(v)) continue;
			if(!col[v]) {
				col[v]=2,pre[v]=u;
				if(!match[v]) return Switch(v),1;
				col[match[v]]=1,que.push(match[v]);
			} else if(col[u]==col[v]) {
				//cout<<"lcaing "<<u<<\' \'<<v<<endl;
				int lca=LCA(u,v);
				//cout<<"shrink!!!"<<u<<\' \'<<v<<\' \'<<lca<<endl;
				// the path has two parts
				Shrink(u,v,lca);
				Shrink(v,u,lca);
			}
		}
	}
	return 0;
}

int main(){
	n=rd();
	rep(i,1,rd()) {
		int u=rd(),v=rd();
		G[u].pb(v),G[v].pb(u);
	}
	int ans=0;
	rep(i,1,n) ans+=!match[i] && Bfs(i);
	printf("%d\\n",ans);
	rep(i,1,n) printf("%d ",match[i]);
}