为什么要用齐次坐标？

Posted 2021-06-06 MorStar-Lab

1. 什么是齐次坐标？

简单的说，齐次坐标就是在原有坐标上增加一个维度：

\\[\\begin{aligned} (x, y) & \\rightarrow(x, y, 1) \\\\ (x, y, z) & \\rightarrow(x, y, z, 1) \\end{aligned} \\]

关于齐次坐标的介绍可查看随笔——齐次坐标的理解

2. 使用齐次坐标有什么优势？

齐次坐标的使用能大大简化三维空间中的点线面表达方式和旋转平移等操作。

2.1 表示点在直线或平面

如何判断点在直线l上？
在2D平面上，一条直线 l 可以用方程 ax + by + c = 0 来表示，该直线用向量表示的话一般记做

\\[l = (a, b, c)^{T} \\]

我们知道点p=(x, y)在直线 l 上的充分必要条件是 ax + by + c = 0，如果使用齐次坐标的话，点p的齐次坐标就是
p\'=(x, y, 1)
那么 ax + by + c = 0 就可以用两个向量的内积（点乘）来表示：

\\[a x+b y+c=(a, b, c)^{T}(x, y, 1)=l^{T} * p^{\\prime}=0 \\]

因此，点p在直线l上的充分必要条件就是 直线l 与p的齐次坐标p\'的内积为零，即 \\(l^{T} * p^{\\prime}=0\\)

如何判断点在平面A上？
三维空间的一个平面A可以用方程 ax + by + cz + d = 0 来表示，三维空间的一个点P=(x, y, z) 的齐次坐标 P\'=(x, y, z, 1)
类似的，点P在空间平面A上可用两个向量的内积表示：

\\[a x+b y+cz+d=(a, b, c, d)^{T}(x, y, z, 1)=A^{T} * P^{\\prime}=0 \\]

因此，点P在平面A上的充分必要条件就是 平面A 向量与P的齐次坐标的内积（点乘）为零：\\(A^{T} * P^{\\prime}=0\\)

2.2 表示直线与直线的交点

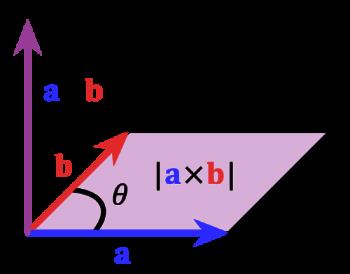
叉乘（也称叉积、外积）的概念：两个向量 a和b 的叉乘仅在三维空间中有定义，记为a x b，a x b 是与向量 a, b都垂直的向量，其方向通过右手定则决定。其模长等于以两个向量为边的平行四边形的面积。
叉乘可以定义为：\\(||a \\times b|| = ||a||*||b||sin(θ)\\)

点乘（也称点积，内积）的定义：\\(a * b = ||a|| * ||b||cos(θ)\\)

由于

\\[\\begin{array}{c} l^{T} *(l \\times m)=l^{T} * p=0 \\\\ m^{T} *(l \\times m)=m^{T} * p=0 \\end{array} \\]

所以，两条直线 \\(l, m\\) 的叉乘表示他们的交点x：\\(x = l \\times m\\)，此处 p 是齐次坐标。
同样可以证明

\\[\\begin{array}{c} (p \\times q)^{T} *p=l^{T} * p=0 \\\\ (p \\times q)^{T} *q=l^{T} * q=0 \\end{array} \\]

所以两点\\(p, q\\)的叉乘 可以表示 过两点的直线l，即 \\(l = p \\times q\\)

2.3 能够区分向量和点

先给出结论：

1. 从普通坐标转换成齐次坐标时
   如果(x,y,z)是个点，则变为(x,y,z,1);
   如果(x,y,z)是个向量，则变为(x,y,z,0)
2. 从齐次坐标转换成普通坐标时
   如果是(x,y,z,1)，则知道它是个点，变成(x,y,z);
   如果是(x,y,z,0)，则知道它是个向量，仍然变成(x,y,z)

具体的解释见：https://www.cnblogs.com/csyisong/archive/2008/12/09/1351372.html

2.4 能够表示无穷远

比如 两条平行的直线 ax+by+c=0, ax+by+d=0，
可分别用向量 l = (a, b, c), m = (a, b,d) 表示，根据前面直线交点的计算方法，其交点为 l x m = (d-c)(b,-a,0)，这里可以去掉标量得到点(b,-a,0)，齐次坐标转化为非齐次坐标得到 (b/0, a/0)，坐标是无穷大，可以认为该点为无穷远点，这与我们通常理解的：平行线相交于无穷远的概念相吻合。

2.5 更简洁的表达欧式空间变换

使用齐次坐标，可以方便的将加法转化为乘法，方便表达平移。
比如将2D坐标点x=[u,v] 平移t=[\\(t_u, t_v\\)]，如果用非齐次方法：

\\[x^{\\prime} \\rightarrow\\left[\\begin{array}{l} u^{\\prime} \\\\ v^{\\prime} \\end{array}\\right]=\\left[\\begin{array}{l} u+t_{u} \\\\ v+t_{v} \\end{array}\\right]=x+t \\]

而用齐次坐标表示时可以将加法转换为乘法

\\[x^{\\prime} \\rightarrow\\left[\\begin{array}{l} u^{\\prime} \\\\ v^{\\prime} \\\\ 1 \\end{array}\\right]=\\left[\\begin{array}{lll} 1 & 0 & t_{u} \\\\ 0 & 1 & t_{v} \\\\ 0 & 0 & 1 \\end{array}\\right]\\left[\\begin{array}{l} u \\\\ v \\\\ 1 \\end{array}\\right]=T x \\]

Reference

https://blog.csdn.net/electech6/article/details/83315237
https://blog.csdn.net/piupiu78/article/details/115663360