二叉堆

Posted 2021-06-06 100001

二叉堆是一种插入、删除、查询最值的数据结构。它其实是一棵满足“堆性质”的完全二叉树，树上的每个节点带有一个权值。

一、若树中的任意一个节点的权值都小于等于其父节点的权值，则称该二叉树满足“大根堆性质”。

二、若树中的任意一个节点的权值都大于等于其父节点的权值，则称该二叉树满足“小根堆性质”。

以下是小根堆的相关操作：
1.插入操作以及调整

 

 1 int heap[size],n;
 2 void up(int p){ //插入到末尾，再向上调整
 3     while(p>1){
 4         if(heap[p]<heap[p/2]){
 5             swap(heap[p],heap[p/2]);
 6             p=p/2;
 7         }
 8         else
 9             break;
10     }
11 }
12 void insert(int val){
13     heap[++n]=val;
14     up(n);
15 }

 

2.获取堆顶元素

1 int GetTop(){
2     return heap[1];
3 }

3.删除堆顶元素

Extract操作把堆顶从二叉堆中移除。我们把堆顶heap[1]与存储在数组末尾的节点heap[n]交换，然后移除数组末尾的节点（令n减小1），最后把堆顶元素通过交换的方式向下调整，直至满足堆性质。其时间复制度为堆的深度，即O（logN）。

 1 void down（int p）{
 2     int s=2*p;
 3     if(s<=n){
 4         if(s<n&&heap[s]>heap[s++]) s++;
 5         if(heap[s]<heap[p]) {
 6             swap(heap[s],heap[p]);
 7             p=s,s=2*p;
 8         }
 9         else
10             break;
11     }
12 }
13 void Extract(){
14     heap[1]=heap[n--];
15     down(1);
16 }

4.删除位置为P的节点。该操作与Extract相似，先把heap[p]与heap[n]交换，然后令n 减小1。注意此时heap[p]既有可能需要向下调整，也有可能需要向上调整，需要分别进行检查和处理。时间复杂度为O（logN）。

1 void Remove(int k){
2     heap[k]=heap[n--];
3     up(k),down(k);
4 }

相关题目：

1.牛客网 rating

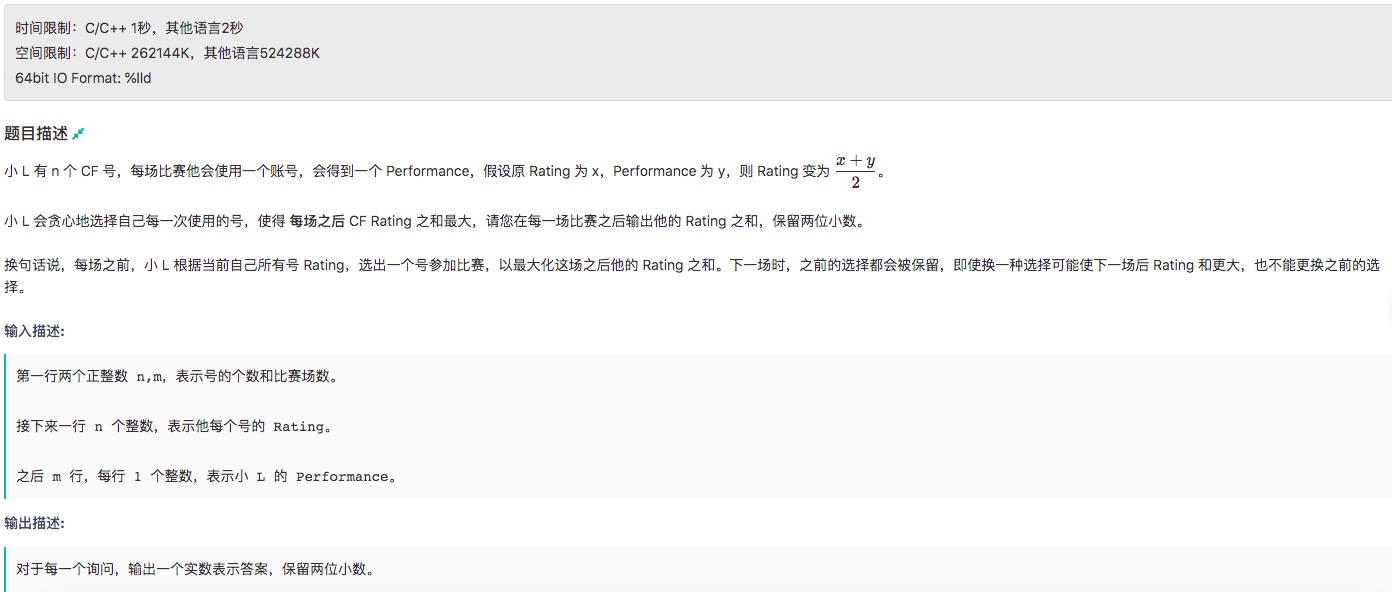
输入

5 5
2000 2100 2200 2300 2350
1900
1500
2200
2700
2000

 

输出

10900.00
10675.00
10912.50
11281.25
11231.25

 

说明

解析：每次选择当前帐号最小的rating，就能确保每场比赛之后的rating之和最大。代码如下：

 1 #include<iostream>
 2 using namespace std;
 3 int a[100005],n;
 4 double heap[100005];
 5 void up(int p){
 6     while(p>1){
 7         if(heap[p]<heap[p/2]) {
 8             swap(heap[p],heap[p/2]);
 9             p=p/2;
10         }
11         else
12             break;
13     }
14 }
15 void Insert(double val){ //val必须为double
16     heap[++n]=val;
17     up(n);
18 }
19 double Gettop(){ //函数返回值为double
20     return heap[1];
21 }
22 void down(int p){
23     int s=p*2;
24     while(s<=n){
25         if(s<n&&heap[s]>heap[s+1]) s++;
26         if(heap[s]<heap[p]) 
27             {
28             swap(heap[s],heap[p]);
29             p=s,s=2*p;}
30         else
31             break;}
32 }
33 void Extract(){
34     heap[1]=heap[n--];
35     down(1);
36 }
37 int num,m;
38 double ans;
39 int main(){
40     cin>>num>>m;
41     for(int i=1;i<=num;i++)
42     {
43         cin>>a[i];
44         ans=ans+a[i];
45         Insert(a[i]);
46     }
47     for(int i=1;i<=m;i++){
48         double x;
49         int y;
50         double rating;
51         x=Gettop();
52         ans=ans-x;
53         cin>>y;
54         rating=(x+y)/2.0;
55         Extract();
56         Insert(rating);
57         ans=ans+rating;
58         printf("%0.2lf\\n",ans);
59     }
60     return 0;
61 }