信道均衡之非线性均衡——噪声预测技术

Posted 2021-06-05 波波葡

　　在通讯系统中，信道是影响信号传输质量的最重要因素，而信道均衡目的是则为了消除信道的影响。 

　　匹配滤波器，迫零滤波器和MMSE滤波器都是线性滤波器，基于这些滤波器的均衡称为线性均衡。通过利用非线性判决器的输出结果，可以进一步提升系统的性能，这种利用判决器结果的均衡称为非线性均衡。非线性均衡后，通信系统的性能可以达到香农极限。

　　这里先介绍噪声预测技术。如图1所示我们将通信系统建模成离散时间系统，并将迫零滤波器用作接收滤波器。信道噪声n(k)是高斯白噪声，由于接收滤波器的作用，y(k)中的噪声部分y_n(k)不再是高斯白噪声，即y_n(k)是相关的。正是这种噪声的相关性，使得我们可以通过预测器来预测噪声。

　　如果整个系统的信号传输没有出现错误，不考虑b(k)与m(k)之间的延迟，那么b(k)=m(k)。 如图2所示，将y(k)与b(k)相减可以得到y(k)中的噪声部分y_n(k)，使用一个FIR噪声预测器P(z)来处理过去的噪声数据，可以预测得到的当前的噪声大小y_np(k)，然后从y(k)中将y_np(k)扣除掉。通过这种方式，判决器的输入sl(k)中的噪声相关部分都被消除掉了，只剩下不相关的白噪声，噪声达到了最小化。噪声预测技术相当于一个将噪声白化和最小化的过程。

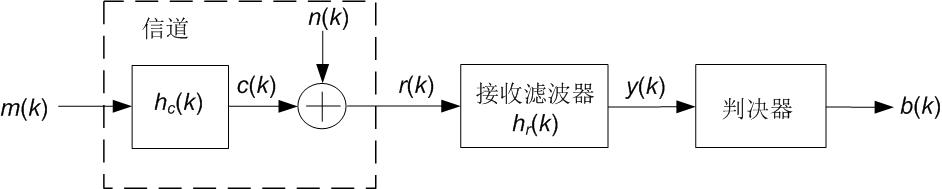
图1 基带通信系统

 

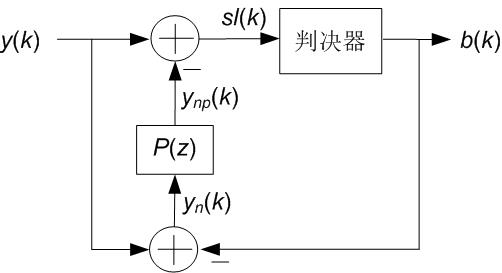
图2 噪声预测技术

 

　　下面我们从数学上来看如何进行噪声的最小化，由于信道h_c(k)引入的ISI已经被接收滤波器h_r(k)消除掉，所以

　　　　

 　　信道无误差传送的情况下

　　　　

　　　　

　　判决器(slicer)的输入为

 　　　　

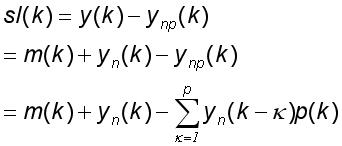
 　　我们想要

　　　　

　　实际上这并不能做到，因为：1，白噪声部分是无法预测的；2，噪声预测并不完全准确。

　　但是我们只要调整噪声预测滤波器P(z)的系数，使得剩余噪声的均方值（下式）最小即可

　　　　

 　　MMSE算法可以用来求此最小化过程。

　　如图3所示，可以将噪声预测技术进行一些等效变换。变换后

　　　　

　　图3(c)就是迫零判决反馈均衡（Zero Forcing Decision Feedback Equalization，ZF-DFE)技术。

　　

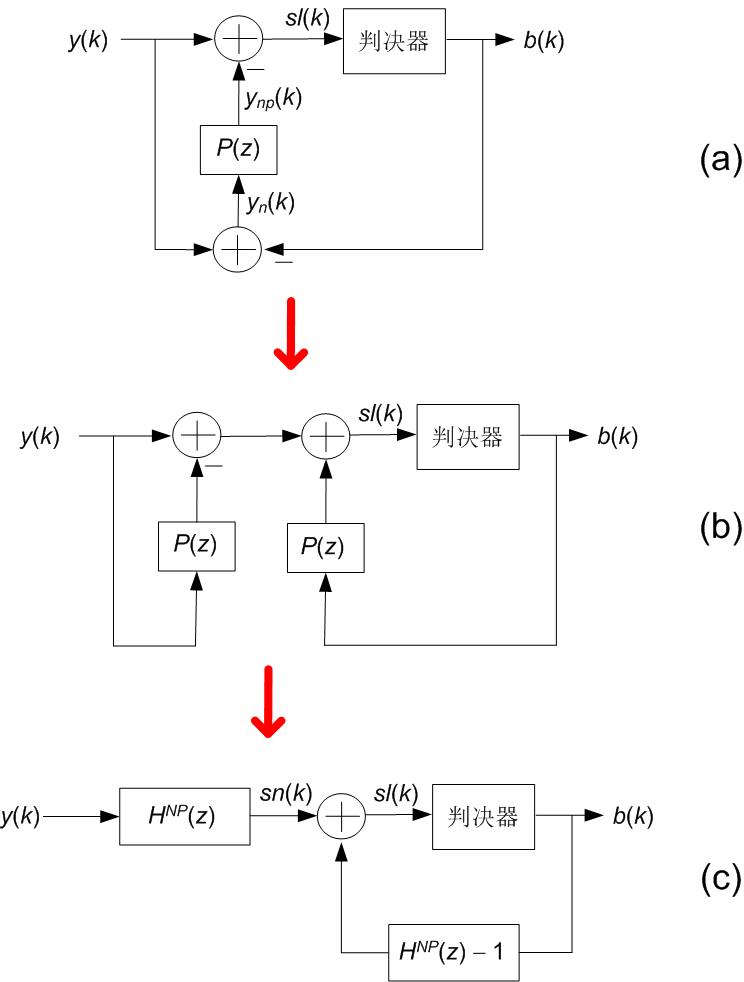
图3 噪声预测技术的等效变换

 

　　信号y(k)已经经过了迫零滤波器，所以y(k)中没有ISI。图3(c)中,  y(k)经过H^NP(z)后，sn(k)又有了ISI。 判决器的输出b(k)经过反馈滤波后，又将这些H^NP(z)引入的ISI消除了，并且由于噪声预测技术，噪声已经被最小化。因此迫零DFE技术可以达到比较好的性能。

　　也许有人会有疑问，只有判决器判决正确的时候才有上述结论，但是sl(k) 中存在噪声，判决器不会出错吗？当然会。如果考虑判决器出错，则反馈回来的信号也是错的，无法准确预测噪声，还会产生误差传递过程，分析非常复杂。我们要做得是使得判决器的判决（尽量）不出错，这个在1比特传输系统（如PAM2 SERDES)中是比较容易做到的。

　　对理论计算感兴趣的读者可以参考Robert F. H. Fiscber的“Precoding and Signal Shaping for Digital Transmission"。

 

作者：波波葡

出处：波波葡 - 博客园 (cnblogs.com)