通过二分查找+位运算求完全二叉树的节点个数

Posted 2021-06-05 小鹏说

前言——什么是完全二叉树

定义：

一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。

性质：

1、具有n个结点的完全二叉树的深度（注：[ ]表示向下取整）

2、如果对一棵有n个结点的完全二叉树的结点按层序编号, 则对任一结点i (1≤i≤n) 有：

• 如果i=1, 则结点i是二叉树的根, 无双亲;如果i>1, 则其双亲parent (i) 是结点[i/2]
• 如果2i>n, 则结点i无左孩子, 否则其左孩子lchild (i) 是结点2i;
• 如果2i+1>n, 则结点i无右孩子, 否则其右孩子rchild (i) 是结点2i+1. 

特点：

完全二叉树的特点：叶子结点只能出现在最下层和次下层，且最下层的叶子结点集中在树的左部。需要注意的是，满二叉树肯定是完全二叉树，而完全二叉树不一定是满二叉树。

 

朴素法

简单来说，其实就是利用Java提供的队列Deque通过层次遍历一遍完全二叉树就可将其节点个数求解出来，时间复杂度为：O(n) (n 为节点个数)

 1 class Solution {
 2     public int countNodes(TreeNode root) {
 3         if (root == null) {
 4             return 0;
 5         }
 6         if (root.left == null && root.right == null) {
 7             return 1;
 8         }
 9 
10         int res = 0;
11         Deque<TreeNode> queue = new LinkedList<>();
12         queue.add(root);
13         while (queue.size() > 0) {
14             TreeNode cur = queue.poll();
15             res++;
16             if (cur.left != null) {
17                 queue.add(cur.left);
18             }
19             if (cur.right != null) {
20                 queue.add(cur.right);
21             }
22         }
23         return res;
24     }
25 }

二分查找+位运算

leetcode题——222. 完全二叉树的节点个数

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。


示例 1：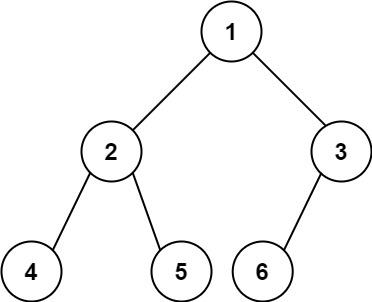

输入：root = [1,2,3,4,5,6]
输出：6

示例 2：

输入：root = []
输出：0

示例 3：

输入：root = [1]
输出：1

提示：

    树中节点的数目范围是[0, 5 * 104]
    0 <= Node.val <= 5 * 104
    题目数据保证输入的树是 完全二叉树

进阶：遍历树来统计节点是一种时间复杂度为 O(n) 的简单解决方案。你可以设计一个更快的算法吗？

解题思路

对于任意二叉树，都可以通过广度优先搜索或深度优先搜索计算节点个数，时间复杂度和空间复杂度都是 O(n)，其中 n 是二叉树的节点个数。这道题规定了给出的是完全二叉树，因此可以利用完全二叉树的特性计算节点个数。

如何计算出二分的左右边界？

力扣官方题解

如何判断第 k 个节点是否存在呢？

如果第 k 个节点位于第 h 层，则 k 的二进制表示包含 h+1 位，其中最高位是 1，其余各位从高到低表示从根节点到第 k 个节点的路径，0 表示移动到左子节点，1 表示移动到右子节点。通过位运算得到第 k 个节点对应的路径，判断该路径对应的节点是否存在，即可判断第 k 个节点是否存在。

 1 class Solution {
 2     public int countNodes(TreeNode root) {
 3         if (root == null) {
 4             return 0;
 5         }
 6         int level = 0;
 7         TreeNode node = root;
 8         while (node.left != null) {
 9             level++;
10             node = node.left;
11         }
12         int low = 1 << level, high = (1 << (level + 1)) - 1;
13         while (low < high) {
14             // 传统写法 ==> (high + low) / 2 后来才发现这种写法可能会溢出
15             // 防止溢出的写法 ==> (high + 2low - low) / 2 ==> (high - low) / 2 + low
16             int mid = (high - low + 1) / 2 + low;
17             if (exists(root, level, mid)) {
18                 low = mid;
19             } else {
20                 high = mid - 1;
21             }
22         }
23         return low;
24     }
25 
26     public boolean exists(TreeNode root, int level, int k) {
27         // k总共有level + 1位，要比较的只有level位，所以左移level - 1位即可（此时就保证了可以比较level位）
28         int bits = 1 << (level - 1);
29         TreeNode p = root;
30         // 要满足两个条件，才能继续比较
31         while (p != null && bits > 0) {
32             // k与bits按位与，比较，当前位是否为0，若为0，则往左走，反之，则为1，往右走
33             if ((bits & k) == 0) {
34                 p = p.left;
35             } else {
36                 p = p.right;
37             }
38             // 每比完一位之后，就将bits向右移动一位.
39             bits >>= 1;
40         }
41         // 最后判断一下此时的p是否为null，因为上面的while循环结束条件可能是p==null结束，也可能是bits == 0结束
42         // 如果比完了，比到bits已经为0了，p还是不为空的话，那么就说明k存在
43         return p != null;
44     }
45 }