数据挖掘实践（52）：adaboost 推导实例

Posted 2021-06-04 秋华

来源：https://blog.csdn.net/guyuealian/article/details/70995333

一 AdaBoost算法过程

　　 给定训练数据集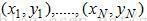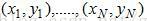：，其中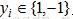用于表示训练样本的类别标签，i=1,...,N。Adaboost的目的就是从训练数据中学习一系列弱分类器或基本分类器，然后将这些弱分类器组合成一个强分类器。

相关符号定义：

 

 

 Adaboost的算法流程如下：

 

 

 

 

 

 

 

 

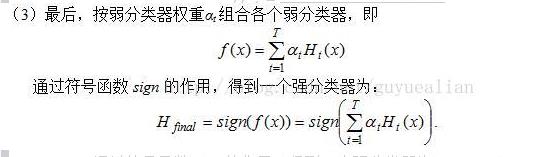
 相关说明：

 

 

 综合上面的推导，可得样本分错与分对时，其权值更新的公式为：

 

 

 

 

 

 

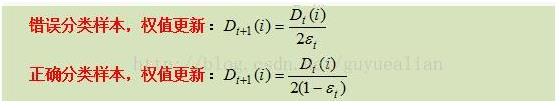
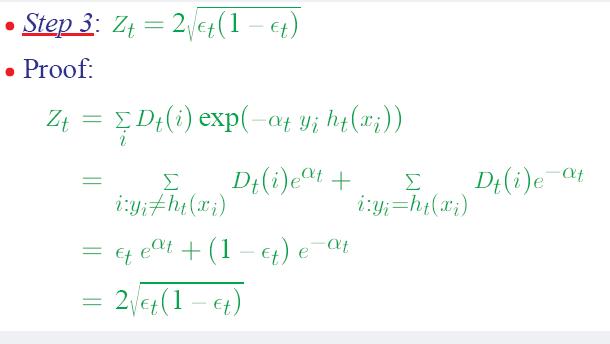
二 AdaBoost实例讲解

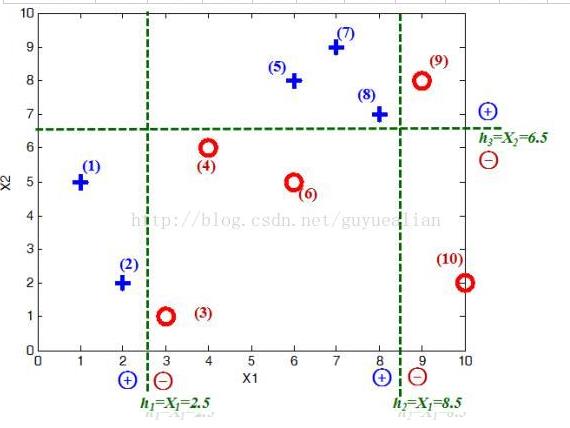
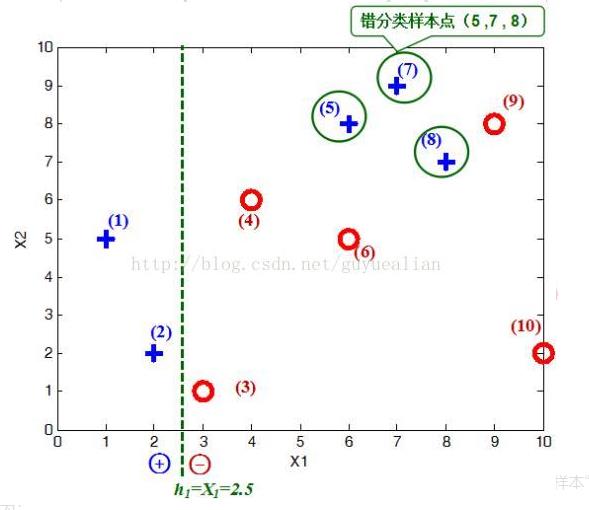
 例：给定如图所示的训练样本，弱分类器采用平行于坐标轴的直线，用Adaboost算法的实现强分类过程。

 

 

 

1） 数据分析：

   　　将这10个样本作为训练数据，根据 X 和Y 的对应关系，可把这10个数据分为两类，图中用“+”表示类别1，用“O”表示类别-1。本例使用水平或者垂直的直线作为分类器，图中已经给出了三个弱分类器，即：

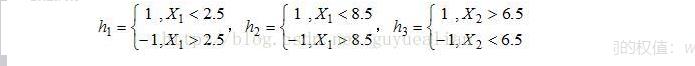2） 初始化：

  　　首先需要初始化训练样本数据的权值分布，每一个训练样本最开始时都被赋予相同的权值：wi=1/N，这样训练样本集的初始权值分布D1(i)：

 　　令每个权值w1i = 1/N = 0.1，其中，N = 10，i = 1,2, ..., 10，然后分别对于t= 1,2,3, ...等值进行迭代（t 表示迭代次数，表示第t轮），下表已经给出训练样本的权值分布情况：

 

 

 

第1次迭代t=1：

  初试的权值分布D1为1/N（10个数据，每个数据的权值皆初始化为0.1），

                                                       D1=[0.1,  0.1, 0.1, 0.1, 0.1, 0.1,0.1, 0.1, 0.1, 0.1]

  在权值分布D1的情况下，取已知的三个弱分类器h1、h2和h3中误差率最小的分类器作为第1个基本分类器H1(x)（三个弱分类器的误差率都是0.3，那就取第1个吧）

 

 

   在分类器H1(x)=h1情况下，样本点“5 7 8”被错分，因此基本分类器H1(x)的误差率为：

 

 

 可见，被误分类样本的权值之和影响误差率e，误差率e影响基本分类器在最终分类器中所占的权重α。

　　然后，更新训练样本数据的权值分布，用于下一轮迭代，对于正确分类的训练样本“1 2 3 4 6 9 10”（共7个）的权值更新为：

 　　这样，第1轮迭代后，最后得到各个样本数据新的权值分布：

　　D2=[1/14,1/14,1/14,1/14,1/6,1/14,1/6,1/6,1/14,1/14]

  　  由于样本数据“5 7 8”被H1(x)分错了，所以它们的权值由之前的0.1增大到1/6；反之，其它数据皆被分正确，所以它们的权值皆由之前的0.1减小到1/14，下表给出了权值分布的变换情况：

 

 

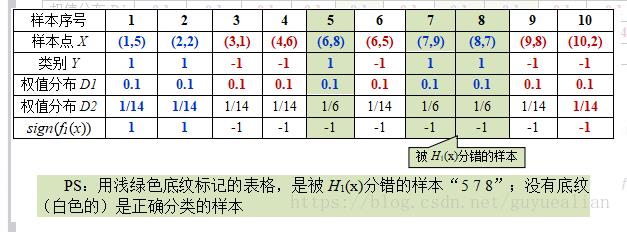
 可得分类函数：f1(x)= α1H1(x) = 0.4236H1(x)。此时，组合一个基本分类器sign(f1(x))作为强分类器在训练数据集上有3个误分类点（即5 7 8），此时强分类器的训练错误为：0.3

第二次迭代t=2：

  在权值分布D2的情况下，再取三个弱分类器h1、h2和h3中误差率最小的分类器作为第2个基本分类器H2(x)：
①　当取弱分类器h1=X1=2.5时，此时被错分的样本点为“5 7 8”：
误差率e=1/6+1/6+1/6=3/6=1/2；
②　当取弱分类器h2=X1=8.5时，此时被错分的样本点为“3 4 6”：
误差率e=1/14+1/14+1/14=3/14；
③　当取弱分类器h3=X2=6.5时，此时被错分的样本点为“1 2 9”：
误差率e=1/14+1/14+1/14=3/14；

 

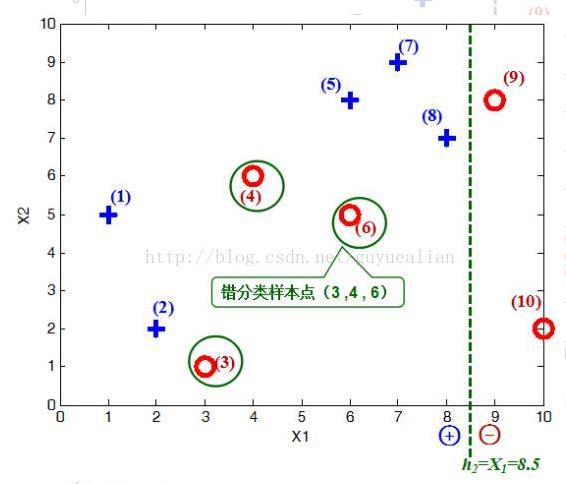
      因此，取当前最小的分类器h2作为第2个基本分类器H2(x)

 

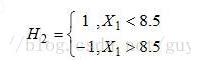
　  显然，H2(x)把样本“3 4 6”分错了，根据D2可知它们的权值为D2(3)=1/14，D2(4)=1/14， D2(6)=1/14，所以H2(x)在训练数据集上的误差率：

 

 

  这样，第2轮迭代后，最后得到各个样本数据新的权值分布：

                                           D3=[1/22,1/22,1/6,1/6,7/66,1/6,7/66,7/66,1/22,1/22]

  下表给出了权值分布的变换情况：

 

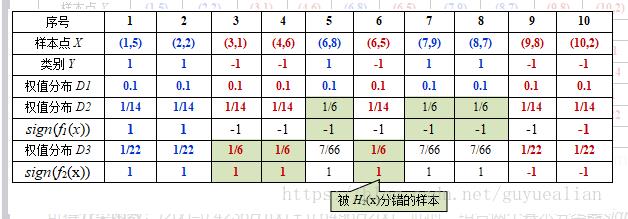
 可得分类函数：f2(x)=0.4236H1(x) + 0.6496H2(x)。此时，组合两个基本分类器sign(f2(x))作为强分类器在训练数据集上有3个误分类点（即3 4 6），此时强分类器的训练错误为：0.3

第三次迭代t=3:

  在权值分布D3的情况下，再取三个弱分类器h1、h2和h3中误差率最小的分类器作为第3个基本分类器H3(x)：
①　当取弱分类器h1=X1=2.5时，此时被错分的样本点为“5 7 8”：
误差率e=7/66+7/66+7/66=7/22；
②　当取弱分类器h2=X1=8.5时，此时被错分的样本点为“3 4 6”：
误差率e=1/6+1/6+1/6=1/2=0.5；
③　当取弱分类器h3=X2=6.5时，此时被错分的样本点为“1 2 9”：
误差率e=1/22+1/22+1/22=3/22；

 

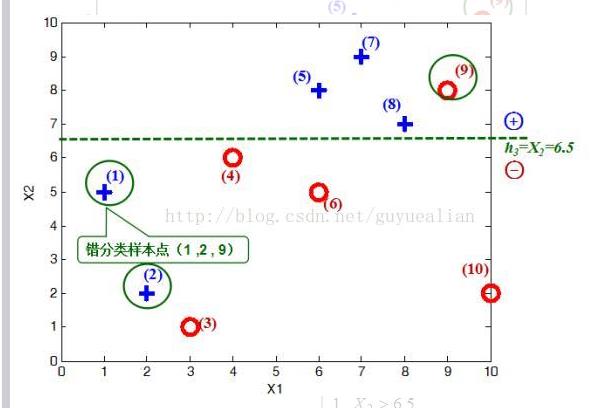
   因此，取当前最小的分类器h3作为第3个基本分类器H3(x)：

  这样，第3轮迭代后，得到各个样本数据新的权值分布为：

        D4=[1/6,1/6,11/114,11/114,7/114,11/114,7/114,7/114,1/6,1/38]

  下表给出了权值分布的变换情况：

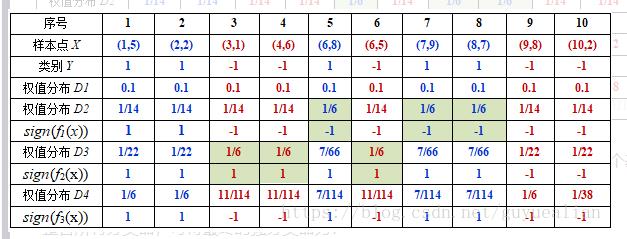
 可得分类函数：f3(x)=0.4236H1(x) + 0.6496H2(x)+0.9229H3(x)。此时，组合三个基本分类器sign(f3(x))作为强分类器，在训练数据集上有0个误分类点。至此，整个训练过程结束。

  整合所有分类器，可得最终的强分类器为：

 

   这个强分类器Hfinal对训练样本的错误率为0！