算法——排序——插入排序——希尔排序

Posted 2021-06-04 Sna1lGo

算法——排序——插入排序(2)——希尔排序

 

 

 

 

简单插入排序的问题：

假设：数组 arr = {2,3,4,5,6,1} 这时需要插入的数 1(最小), 这样的过程是： {2,3,4,5,6,6} {2,3,4,5,5,6} {2,3,4,4,5,6} {2,3,3,4,5,6} {2,2,3,4,5,6} {1,2,3,4,5,6} 结论: 当需要插入的数是较小的数时，后移的次数明显增多，对效率有影响。

希尔排序：

希尔排序是希尔（Donald Shell）于1959年提出的一种排序算法。希尔排序也是一种插入排序，它是简单插入排序经过改进之后的一个更高效的版本，也称为缩小增量排序。

希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。也就是按数组的下标选择如何进行分组，然后分别对每个分组进行简答插入排序，直到每个组只有一个内容。也就是说按照步长选择和谁一组，然后对每个组进行插入排序，直到步长为1，也就是所有的数为一组，最后再来一个直接插入排序就好了。相当于就是按照一个规定来分组，然后对分组进行插入排序，直到最后全部是一组再来一次。

 

 

 

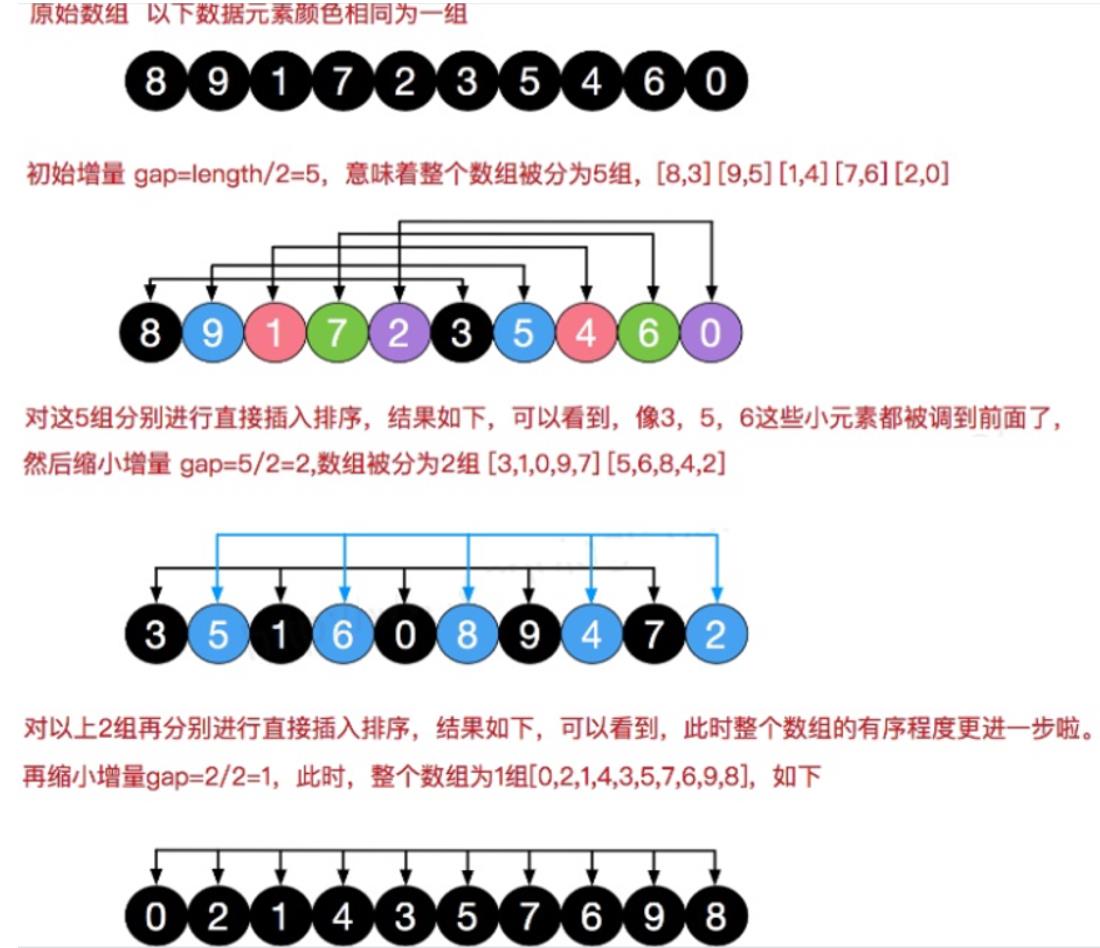
代码实现希尔排序：

原理比较简单，就是利用步长将其分组，然后对每个分组内部进行直接插入排序，直到最后步长为一也就是所有元素是一个数组后再来一次希尔排序。

void ShellSort(int* a, int len)
{
    //第一个for循环用来分组，并且计算步长
    for (int Step = len / 2; Step >= 1; Step /= 2)
    {
        //第二个for循环用来获取分组后有多少个分组
        for(int GroupNum = 0;GroupNum<Step;GroupNum++)
        {
            //第三个for循环用来对每个分组进行直接插入排序
            //直接插入排序的第一个for循环用来遍历除了第一个数之外的后面数
            for (int CharuNum = GroupNum + Step; CharuNum < len; CharuNum += Step)
            {
                //第四个for循环用来遍历要插入的位置的前面所有的数
                for (int CompareNum = GroupNum; CompareNum < CharuNum; CompareNum += Step)
                {
                    if (a[CharuNum] < a[CompareNum])
                    {
                        //第五个for循环用来移动
                        int temp = a[CharuNum];
                        for (int Move = CharuNum; Move > CompareNum; Move -= Step)
                        {
                            a[Move] = a[Move - Step];
                        }
                        a[CompareNum] = temp;
                    }
                }
            }
        }
    }
    for (int i = 0; i < len; i++)
    {
        cout << a[i] << " ";
    }
    cout << endl;
}

 

算法效率

希尔排序时间复杂度是 O(n^(1.3-2))，空间复杂度为常数阶 O(1)。希尔排序没有时间复杂度为 O(n(logn)) 的快速排序算法快 ，因此对中等大小规模表现良好，但对规模非常大的数据排序不是最优选择，总之比一般 O(n^2 ) 复杂度的算法快得多。具体的计算方法就比较麻烦了，这里就不展开了。