数据结构--线段树

Posted 2021-06-03 greenofyu

线段树的基本思想是分治。

此处的是简单线段树，即只支持单点修改，区间查询，不涉及懒标记。

树的每一个节点维护一个区间 [ l , r ] 的值，其子节点的区间的并集等于这个区间的值，左儿子维护[l , mid] ，右儿子维护[ mid+1 , r ]。

树的高度为log(n)，所以更新操作的时间复杂度为log(n)。

可以证明，查询操作最多只会涉及4*log(n)个区间。

所以线段树的单次操作复杂度为log(n)

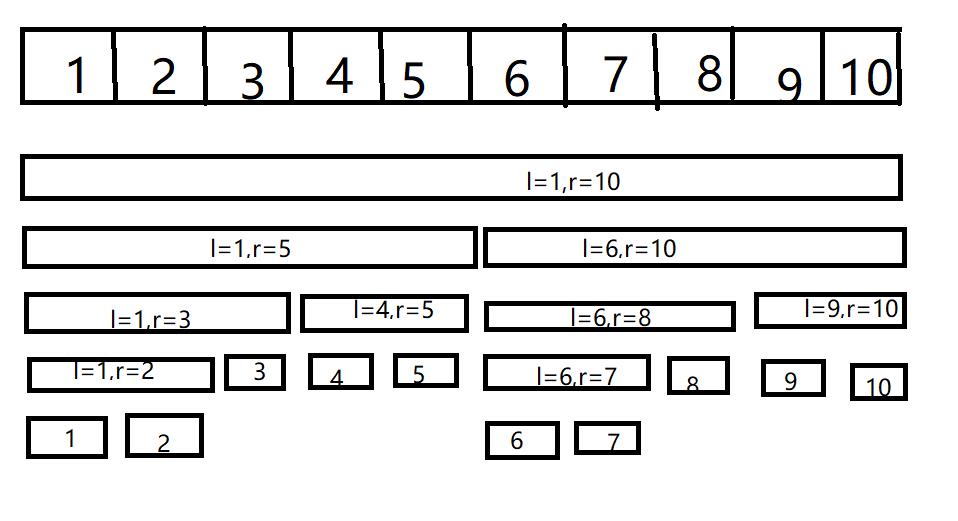
简单线段树包括4大函数：pushup(),build(),modify(),query()

 

 https://www.acwing.com/problem/content/1266/

 1 //单点修改，区间查询线段树4大函数，pushup(),build(),modify(),query()
 2 #include <iostream>
 3 #include <cstring>
 4 #include <algorithm>
 5 using namespace std;
 6 const int N=100010;
 7 int w[N];
 8 int n,m;
 9 struct node{
10     int l,r;
11     int sum;
12 }tr[N * 4];
13 void pushup(int u){//用u的两个子节点的信息来更新u
14     tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;
15 }
16 void build(int u,int l,int r){//构建线段树
17     if(l==r) tr[u]={l,r,w[l]};
18     else{
19         tr[u].l=l,tr[u].r=r;
20         int mid=l+r>>1;
21         build(u<<1,l,mid);
22         build(u<<1|1,mid+1,r);
23         pushup(u);
24     }
25 }
26 int query(int u,int l,int r){//查询l，r的信息
27     if(tr[u].l>=l&&tr[u].r<=r) return tr[u].sum;
28     else{
29         int mid=tr[u].l+tr[u].r>>1;
30         int sum=0;
31         if(l<=mid) sum+=query(u<<1,l,r);
32         if(r>=mid+1) sum+=query(u<<1|1,l,r);
33         return sum;
34     }
35 }
36 void modify(int u,int p,int v){//修改p位置的信息
37     if(tr[u].l==tr[u].r) tr[u].sum+=v;
38     else{
39         int mid=tr[u].l+tr[u].r>>1;
40         if(p<=mid) modify(u<<1,p,v);
41         else modify(u<<1|1,p,v);
42         pushup(u);
43     }
44 }
45 int main(void){
46     cin>>n>>m;
47     for(int i=1;i<=n;i++){
48         cin>>w[i];
49     }
50     build(1,1,n);
51     while(m--){
52         int k,x,y;
53         cin>>k>>x>>y;
54         if(k==0) cout<<query(1,x,y)<<endl;
55         else if(k==1) modify(1,x,y);
56     }
57     return 0;
58 }