STM32使用K型热电偶测温：运算放大器+内置ADC+K型热电偶分度表+中间温度定律 | K型热电偶的温度-热电势曲线

Posted 2021-06-01 蔡子CaiZi

1.理论部分

1.1分度表

使用Python绘制温度-热电势曲线

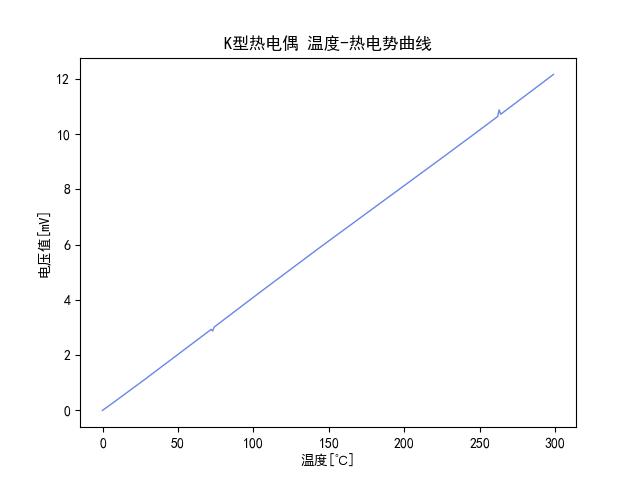
 1 from pylab import *
 2 \'\'\'绘制K型分度表曲线0-299度\'\'\'
 3 xTemp = [temp for temp in range(300)]
 4 yK = [0,0.039,0.079,0.119,0.158,0.198,0.238,0.277,0.317,0.357,
 5 0.397,0.437,0.477,0.517,0.557,0.597,0.637,0.677,0.718,0.758,
 6 0.798,0.838,0.879,0.919,0.960,1.000,1.041,1.081,1.122,1.162,
 7 1.203,1.244,1.285,1.325,1.366,1.407,1.448,1.489,1.529,1.570,
 8 1.611,1.652,1.693,1.734,1.776,1.817,1.858,1.899,1.940,1.981,
 9 2.022,2.064,2.105,2.146,2.188,2.229,2.270,2.312,2.353,2.394,
10 2.436,2.477,2.519,2.560,2.601,2.643,2.684,2.726,2.767,2.809,
11 2.850,2.892,2.933,2.875,3.016,3.058,3.100,3.141,3.183,3.224,
12 3.266,3.307,3.349,3.390,3.432,3.473,3.515,3.556,3.598,3.639,
13 3.681,3.722,3.764,3.805,3.847,3.888,3.930,3.971,4.012,4.054,
14 4.095,4.137,4.178,4.219,4.261,4.302,4.343,4.384,4.426,4.467,
15 4.508,4.549,4.590,4.632,4.673,4.714,4.755,4.796,4.837,4.878,
16 4.919,4.960,5.001,5.042,5.083,5.124,5.164,5.205,5.246,5.287,
17 5.327,5.368,5.409,5.450,5.490,5.531,5.571,5.612,5.652,5.693,
18 5.733,5.774,5.814,5.855,5.895,5.936,5.976,6.016,6.057,6.097,
19 6.137,6.177,6.218,6.258,6.298,6.338,6.378,6.419,6.459,6.499,
20 6.539,6.579,6.619,6.659,6.699,6.739,6.779,6.819,6.859,6.899,
21 6.939,6.979,7.019,7.059,7.099,7.139,7.179,7.219,7.259,7.299,
22 7.338,7.378,7.418,7.458,7.498,7.538,7.578,7.618,7.658,7.697,
23 7.737,7.777,7.817,7.857,7.897,7.937,7.977,8.017,8.057,8.097,
24 8.137,8.177,8.216,8.256,8.296,8.336,8.376,8.416,8.456,8.497,
25 8.537,8.577,8.617,8.657,8.697,8.737,8.777,8.817,8.857,8.898,
26 8.938,8.978,9.018,9.058,9.099,9.139,9.179,9.220,9.260,9.300,
27 9.341,9.381,9.421,9.462,9.502,9.543,9.583,9.624,9.664,9.705,
28 9.745,9.786,9.826,9.867,9.907,9.948,9.989,10.029,10.070,10.111,
29 10.151,10.192,10.233,10.274,10.315,10.355,10.396,10.437,10.478,10.519,
30 10.560,10.600,10.641,10.882,10.723,10.764,10.805,10.848,10.887,10.928,
31 10.969,11.010,11.051,11.093,11.134,11.175,11.216,11.257,11.298,11.339,
32 11.381,11.422,11.463,11.504,11.545,11.587,11.628,11.669,11.711,11.752,
33 11.793,11.835,11.876,11.918,11.959,12.000,12.042,12.083,12.125,12.166]
34 mpl.rcParams[\'font.sans-serif\'] = [\'SimHei\']  # 添加这条可以让图形显示中文
35 plt.plot(xTemp, yK, \'r-\', color=\'#4169E1\', alpha=0.8, linewidth=1)
36 plt.xlabel(\'温度[℃]\')
37 plt.ylabel(\'电压值[mV]\')
38 plt.title(\'K型热电偶 温度-热电势曲线\')
39 plt.show()
40 得到如下曲线，不能说是线性度很好吧，可以说就是线性的！只有偶尔几个点有波动，所以大可以直接用斜率计算温度。

 

常用热电偶的拟合多项式系数，对应温度计算公式为：T=A0*U^0+A1*U^1+...+Ai*U^i；其中U为测得的电动势（V），T为热电偶两端的温度（℃）。

 

1.2冷端补偿

上面的K型热电偶分度表的冷端温度是以0℃为参考的，在室温下直接用这个办法肯定是不行的，那么可以去看看中间温度定律，中间温度定律解决了这个问题，唯一的缺陷就是，最好是室温变化小，并且已知室温。室温可以使用一路ADC+NTC热敏电阻采集到。

来自百度百科 中间温度定律