数据结构——堆（heap）

Posted 2021-05-30 二森

一、概念

 说起堆，我们就想起了土堆，把土堆起来，当我们要用土的时候，首先用到最上面的土。类似地，堆其实是一种优先队列，按照某种优先级将数字“堆”起来，每次取得时候从堆顶取。

 堆是一颗完全二叉树，其特点有如下几点：
1.可以使用一维数组来表示。其中，第i个节点的父节点、子节点index如下：
 - parent(i) = (i - 1) / 2; (取整)
 - leftChild(i) = i * 2 + 1；
 - rightChild(i) = i * 2 + 2;
2.堆中某个节点的值总是不大于（最小堆）或不小于（最大堆）其父节点的值

二、上浮（shiftUp）和下沉（shiftDown）

1. 上浮（shiftUp）（以构建最小堆为例）

上浮操作就是，如果一个节点比它父节点小，则将它与父节点交换位置。这个节点在数组中的位置上升。

2. 下沉（shiftDown）

下沉操作就是，如果一个节点比它子节点大，那么它需要向下移动。称之为“下沉”。

三、堆的构建

给定一个一维数组[4,1,3,2,16,9,10,14,8,7]，怎么把它构建成一个堆呢？使用自底向上的方法将数组转化为堆。
大体思路为：如果每一个节点都是一个堆（以这个节点为根），那么这个数组肯定是一个堆。自底向上的方法意思就是，自底向上依次调整每个节点，使得以该节点为根的树是一个堆。
（以最大堆为例）

1. 首先将数组还原成一个完全二叉树
   、
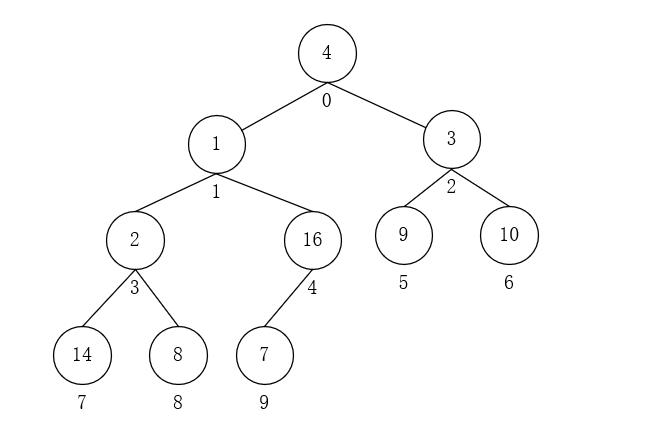2. 从倒数第一个非叶子节点开始（i = (n/2)-1，其中，n是数组的长度），依次对每个节点执行步骤3，将其调整成最大堆，直至第0个节点。
   【这里要说一下为啥从第一个非叶子节点开始，因为叶节点没有孩子节点，可以把它看成只有一个元素的堆。】
3. 将以第i个节点为根节点的子树调整为最大堆。假设根节点A[i]的左右子树的根节点index分别为left[i]和right[i]，其中，left[i]和right[i]都是最大堆。采用逐级下降的方法进行调整，具体步骤如下：
   （1） 从A[i]、A[left[i]]、A[right[i]]中找到最大的值，将其下标存到largest中。如果A[i]是最大的，那么以i为根节点的子树是最大堆；否则，交换A[i]和A[largest]的值。
   （2） 对下标为largest为根的子树重复（1）操作，直至largest为叶子节点。

如图所示：

• 从 i = 4 开始遍历，此时，A[4] = 16，它是一个最大堆；
• i = 3，A[3] = 2，与A[7]交换，因为i = 7是叶子节点，所以调整完毕。
• i = 2，A[2] = 3，与A[6]交换，因为i = 6是叶子节点，所以调整完毕。此时，该树变成：
  
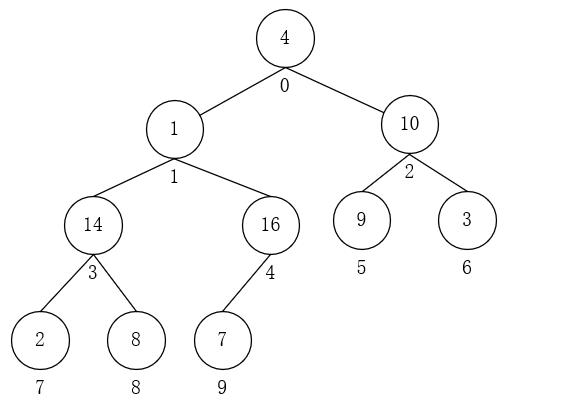
• i = 1，A[1] = 1，与A[4]交换。因为i = 4不是叶子节点，所以要对以4为根的子树进行上述操作；此时，A[4] = 1，与A[9]交换，i = 9是叶子节点，调整完毕。如下图所示：
  
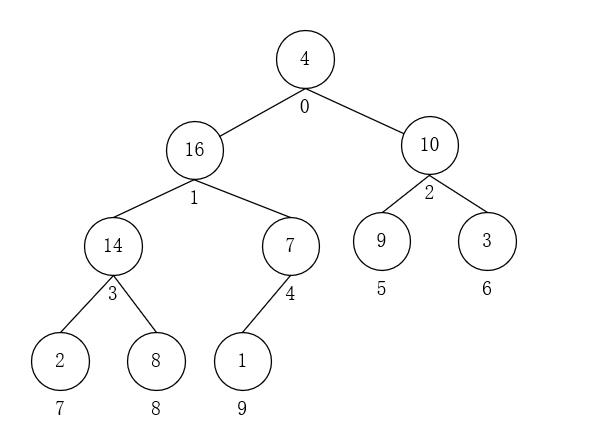
• i = 0，A[0] = 4，与A[1]交换。因为i = 1不是叶子节点，对以1为根的子树进行上述操作；此时，A[1] = 4，与A[3]交换，i = 3不是叶子节点，对以3为根的子树重复进行操作；此时A[3] = 4，与A[8]交换，i = 8是叶子节点，调整完毕。最终得到最大堆：
  

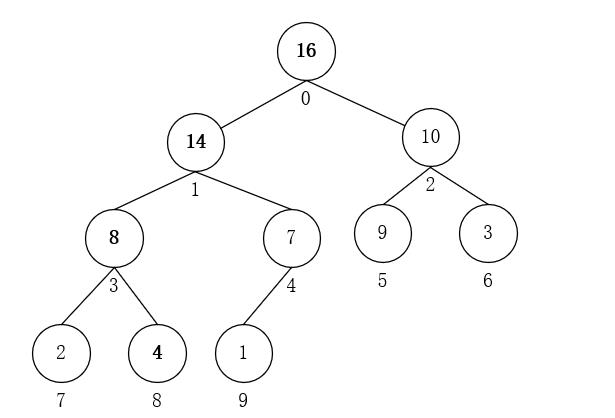
四、堆的其它方法

1.插入

2.删除

五、javascript实现堆类