数据结构与算法——基础篇
Posted 卡斯特梅的雨伞
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构与算法——基础篇相关的知识,希望对你有一定的参考价值。
数据结构与算法——基础篇(二)
希尔排序——Shell Sort——缩小增量排序——O(n log n)
希尔排序也是一种插入排序,它是简单插入排序经过改进之后的一个更高效的版本,也称为缩小增量排序。(希尔排序是把记录按下标的一定增量分组,缩小的是分组的增量,数组增量最后缩小为一组,排序完成)
前提——简单插入排序存在的问题
我们看简单的插入排序可能存在的问题.
数组 arr = {2,3,4,5,6,1} 这时需要插入的数 1(最小), 这样的过程是:
{2,3,4,5,6,6}
{2,3,4,5,5,6}
{2,3,4,4,5,6}
{2,3,3,4,5,6}
{2,2,3,4,5,6}
{1,2,3,4,5,6}
在我们进行简单的插入排序可能存在的问题是待排序的数组中,较小的元素集中在后面,这时候,当我们进行升序排序时,需要插入的数是较小的数时,后移的次数明显增多,对效率有影响。
基本思想
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。
思路分析
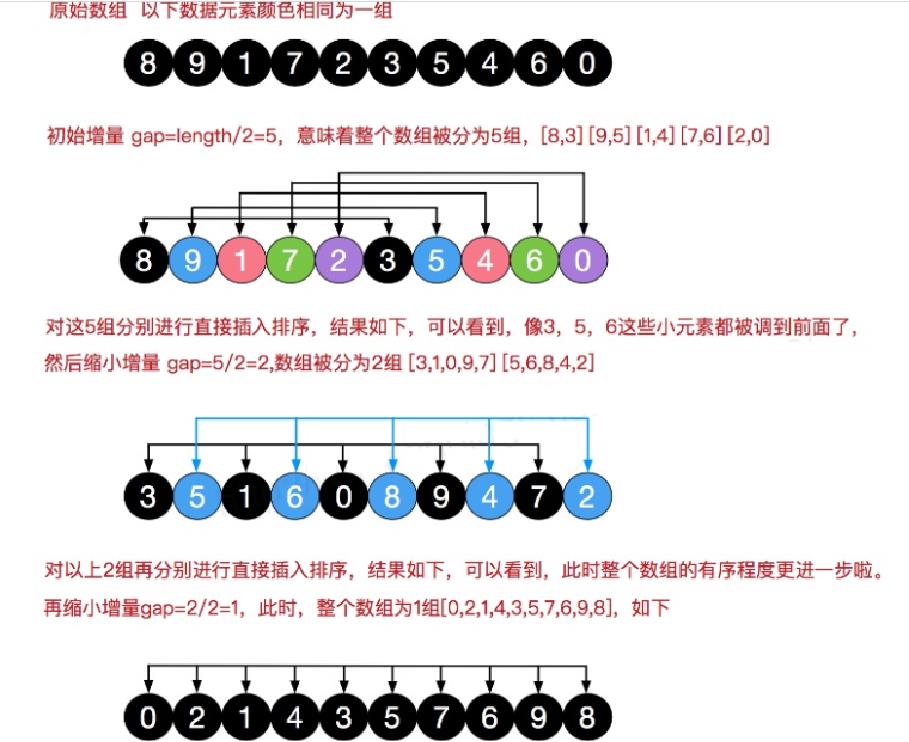

代码示例
希尔排序时, 对有序序列在插入时可以采用交换法或者移动法,正常使用移动法,速度才能上来,也才符合希尔排序的思想是插入排序的一种缩小增量排序的优化。
/**
* 排序前:
* [8, 9, 1, 7, 2, 3, 5, 4, 6, 0]
* 排序后:
* [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
* 十万条数据排序耗时18
*/
public class ShellSort {
public static void main(String[] args) {
int[] array = {8, 9, 1, 7, 2, 3, 5, 4, 6, 0,0,0,0};
System.out.println("排序前:");
System.out.println(Arrays.toString(array));
shellSort(array);
System.out.println("排序后:");
System.out.println(Arrays.toString(array));
int[] arrayTest = new int[10_0000];
for (int i = 0; i < 10_0000; i++) {
arrayTest[i] = (int) (Math.random() * 10_00000);
}
long start = System.currentTimeMillis();
shellSort(arrayTest);
// shellSortBySwap(arrayTest);//十万条数据排序耗时13043
long end = System.currentTimeMillis();
System.out.println("十万条数据排序耗时"+(end-start));
}
/**
* 希尔排序——移动法
* @param array
*/
public static void shellSort(int[] array) {
//gap表示分为几组,5->2->1
for (int gap = array.length / 2; gap > 0; gap /= 2) {
//int i = gap = 10/2=5,就是从5开始,是因为我们做插入排序时,会将数组分为有序表和无序表,5组则有5组有序和无序表,插入排序时从被比较的字段开始
//5个组则待排序从5开始
//第二轮2个组,则默认0,1各为这两个数组的有序表,则待排序元素从2开始
//变量各组中所有的元素,一共gap组,每组2^n个元素,n>=1,步长是gap
for (int i = gap; i < array.length; i++) {
//待插入位置下标
int index = i;
//temp记录待插入值
int temp = array[i];
// if (array[index] < array[index - gap]) {
//如果当前元素小于加上步长后的元素,说明需要进行前移
//注意这里要拿temp与array[index - gap]比较,再进行插入排序前移,如果拿array[index],会因为赋值而导致变化,无法满足比较
while (index - gap >= 0 && temp < array[index - gap]) {
//index - gap的值后移,也就是往后移动gap位置
array[index] = array[index - gap];
//往前移动gap,继续比较,最后gap=1,也就是往前一个个比较,如果temp比之前的数小,就让
index -= gap;
}
//这里不会像插入排序那样导致越界的原因
array[index] = temp;
// }
}
}
}
/**
* 希尔排序——交换法
* @param array
*/
public static void shellSortBySwap(int[] array) {
int temp = 0;
for (int gap = array.length / 2; gap > 0; gap /= 2) {
for (int i = gap; i < array.length; i++) {
for (int j = i - gap; j >= 0; j -= gap) {
if (array[j] > array[j + gap]) {
temp = array[j];
array[j] = array[j + gap];
array[j + gap] = temp;
}
}
}
}
}
}
快速排序—— Quick Sort——冒泡排序的改进——O(n log n)
快速排序(Quicksort)是对冒泡排序的一种改进。
基本思想
通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
思路分析

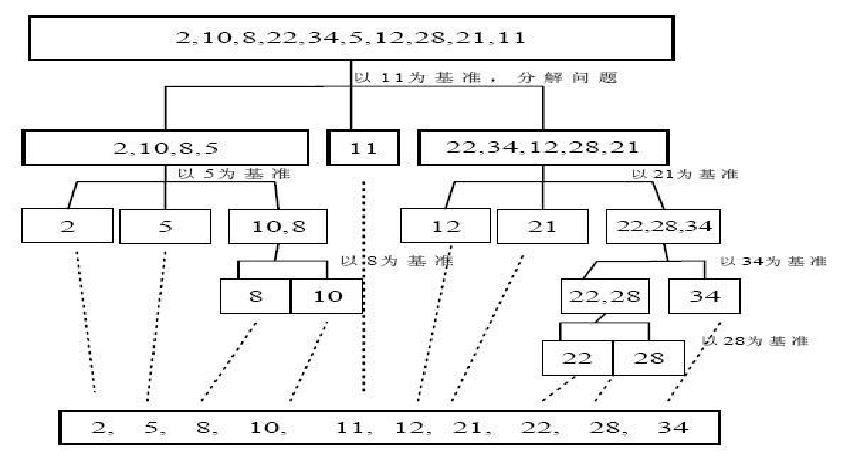
代码示例
/**
* 排序前:
* [-9, 78, 0, 23, -567, 70]
* 排序后:
* [-567, -9, 0, 23, 70, 78]
* 十万条数据排序耗时21
*/
public class QuickSort {
public static void main(String[] args) {
int[] array = {-9, 78, 0, 23, -567, 70};
System.out.println("排序前:");
System.out.println(Arrays.toString(array));
quickSort(array,0,array.length-1);
System.out.println("排序后:");
System.out.println(Arrays.toString(array));
int[] arrayTest = new int[10_0000];
for (int i = 0; i < 10_0000; i++) {
arrayTest[i] = (int) (Math.random() * 10_00000);
}
long start = System.currentTimeMillis();
quickSort(arrayTest,0,arrayTest.length-1);
// shellSortBySwap(arrayTest);//十万条数据排序耗时13043
long end = System.currentTimeMillis();
System.out.println("十万条数据排序耗时"+(end-start));
}
public static void quickSort(int[] array, int left, int right) {
//左下标
int l = left;
//右下标
int r = right;
//中轴值
int pivot = array[(left + right) / 2];
//临时变量swap用
int temp = 0;
//让比中轴值小的在左边
while (l < r) {
//在pivot左边一直找,直到找到大于等于pivot值后退出,得到要交互的左边值位置
while (array[l] < pivot) {
l++;
}
//在pivot右边一直找,直到找到小于等于pivot值后退出,得到要交互的右边值位置
while (pivot < array[r]) {
r--;
}
//l>=r 左右两边值已按pivot左小右大区分
if (l >= r) {
break;
}
//把找到的左右值进行交互
temp = array[l];
array[l] = array[r];
array[r] = temp;
//交换完成后,发现array[l] == pivot值, r--,前移
if (array[l] == pivot) {
r--;
}
//交互完成后,发现array[r] == pivot值, l++,前移
if (array[r] == pivot) {
l++;
}
}
//l==r则表示已经遍历完了,避免栈溢出
if (l == r) {
l++;
r--;
}
//向左递归 r--一直往左边移动,直到r<=left,表示超出最左边的范围
if (left<r){
quickSort(array,left,r);
}
//向右递归 l++一直往右边移动
if (right>l){
quickSort(array,l,right);
}
}
}
归并排序——Merge Sort——分治策略——O(n log n)
合并操作次数= 数组长度-1次,即8个元素需要合并7次。合并操作是线性增长而不是像冒泡那样是O(n^2)这样是平方阶增长。
归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,该算法采用经典的分治策略(divide-and-conquer)(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。
分的过程中仅仅是把数据分开到每个栈中而已,并没有实际的处理,治的过程才是真正在做排序。
归并思想
说明:可以看到这种结构很像一棵完全二叉树,本文的归并排序我们采用递归去实现(也可采用迭代的方式去实现)。分阶段可以理解为就是递归拆分子序列的过程。
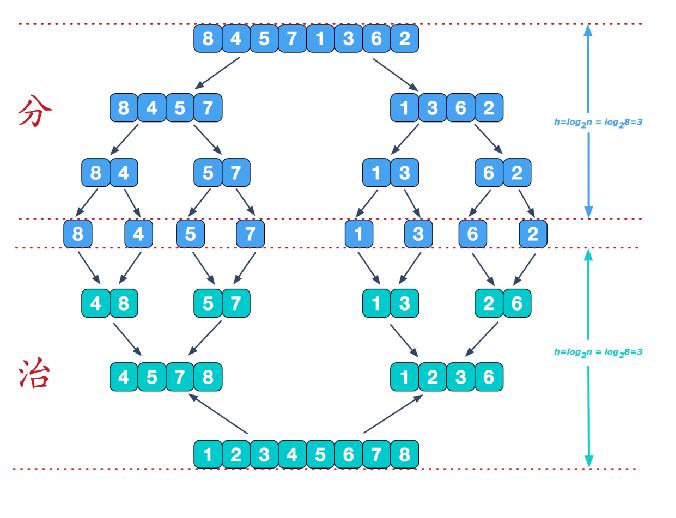
合并思路分析
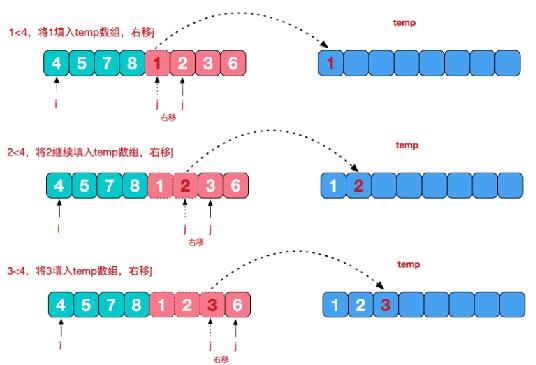
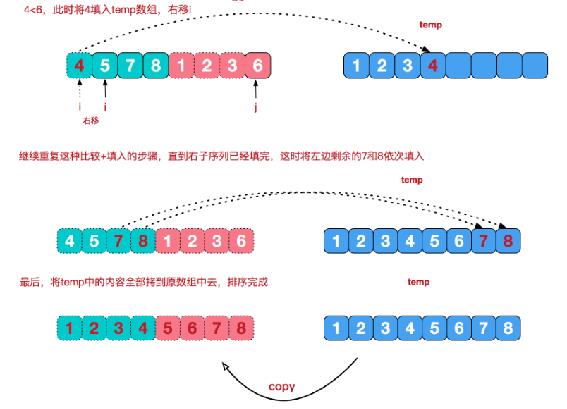
代码示例
/**
* 排序前:
* [8, 4, 5, 7, 1, 3, 6, 2]
* 排序后:
* [1, 2, 3, 4, 5, 6, 7, 8]
* 十万条数据排序耗时18
*/
public class MergeSort {
public static void main(String[] args) {
int[] array = {8, 4, 5, 7, 1, 3, 6, 2};
int[] temp = new int[array.length];
System.out.println("排序前:");
System.out.println(Arrays.toString(array));
mergeSort(array, temp, 0, array.length - 1);
System.out.println("排序后:");
System.out.println(Arrays.toString(array));
int[] arrayTest = new int[10_0000];
int[] tempTest = new int[arrayTest.length];
for (int i = 0; i < 10_0000; i++) {
arrayTest[i] = (int) (Math.random() * 10_0000);
}
long start = System.currentTimeMillis();
//注意传入的数组的左右两端值 arrayTest.length - 1
mergeSort(arrayTest, tempTest, 0, arrayTest.length - 1);
long end = System.currentTimeMillis();
System.out.println("十万条数据排序耗时"+(end-start));
}
public static void mergeSort(int[] array, int[] temp, int left, int right) {
if (left < right) {
//中间索引
int mid = (left + right) / 2;
//向左递归分解
mergeSort(array, temp, left, mid);
//向右递归分解
mergeSort(array, temp, mid + 1, right);
//递归分解后对最后分解的最先合并起来
merge(array, temp, left, mid, right);
}
}
/**
* 合并
* @param array 原始数组
* @param temp 临时存放中转数据的数组
* @param left 分解后的左索引
* @param mid 中间索引
* @param right 分解后的右索引
*/
private static void merge(int[] array, int[] temp, int left, int mid, int right) {
//i,j,t是为了比较两个有序序列里元素的值而定义的数组下标
//i是左边有序序列的初始下标索引
int i = left;
//j是右边有序序列的初始下标索引
int j = mid + 1;
//temp数组的当前下标索引
int t = 0;
//1、将左右两边的有序序列的数据依次通过下标进行比较,把较小的填充到temp数组中,直到有一边有序序列已经处理完毕
while (i <= mid && j <= right) {
if (array[i] < array[j]) {
temp[t] = array[i];
t++;
i++;
} else {
temp[t] = array[j];
t++;
j++;
}
}
//2、这时候我们判断是哪边的有序序列还有剩余元素,把剩余的元素依次填充到temp数组中,因为他们已经是有序的了
while (i <= mid) {
temp[t] = array[i];
t++;
i++;
}
while (j <= right) {
temp[t] = array[j];
t++;
j++;
}
//3、把temp数组的元素拷贝到原始数组array中,值需要拷贝left->right长度的数据即可,不需要全部拷贝
//之所以要新建左端点的局部变量是因为我们要对其遍历++,所以要创建个新的值tempLeft处理好点
int tempLeft = left;
//从0开始获取temp数组元素
t = 0;
while (tempLeft <= right) {
array[tempLeft] = temp[t];
t++;
tempLeft++;
}
}
}
基数排序——Radix Sort——桶排序——包含负数元素不适应
排序数组里有负数不适合处理。对负数要支持的话就是再安排10个桶专门用来存放负数。拿到负数时要对负数求绝对值,再放到对应负数的桶里,等取数的时候再取反处理。
- 基数排序(radix sort)属于“分配式排序”(distribution sort),又称“桶子法”(bucket sort)或bin sort,顾名思义,它是通过键值的各个位的值,将要排序的元素分配至某些“桶”中,达到排序的作用
- 基数排序法是属于稳定性的排序,基数排序法的是效率高的稳定性排序法。
- 基数排序(Radix Sort)是桶排序的扩展。
- 基数排序是1887年赫尔曼·何乐礼发明的。它是这样实现的:将整数按位数切割成不同的数字,然后按每个位数分别比较。
基数排序的说明
- 基数排序是对传统桶排序的扩展,速度很快.
- 基数排序是经典的空间换时间的方式,占用内存很大, 当对海量数据排序时,容易造成 OutOfMemoryError 。
- 基数排序时稳定的。[注:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的]
- 有负数的数组,我们不用基数排序来进行排序, 如果要支持负数,参考
基本思想
将所有待比较数值统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。
思路分析
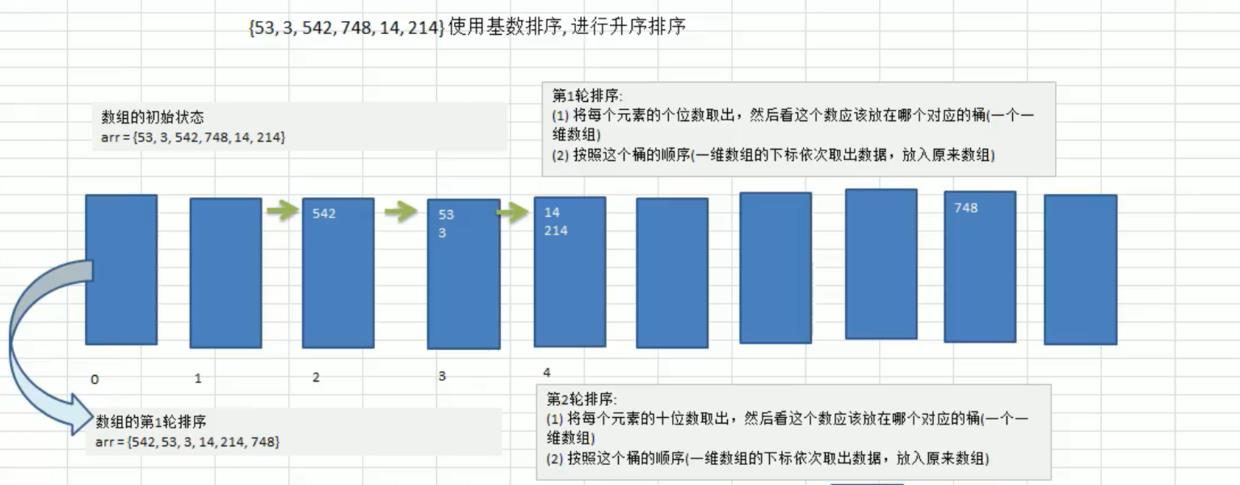
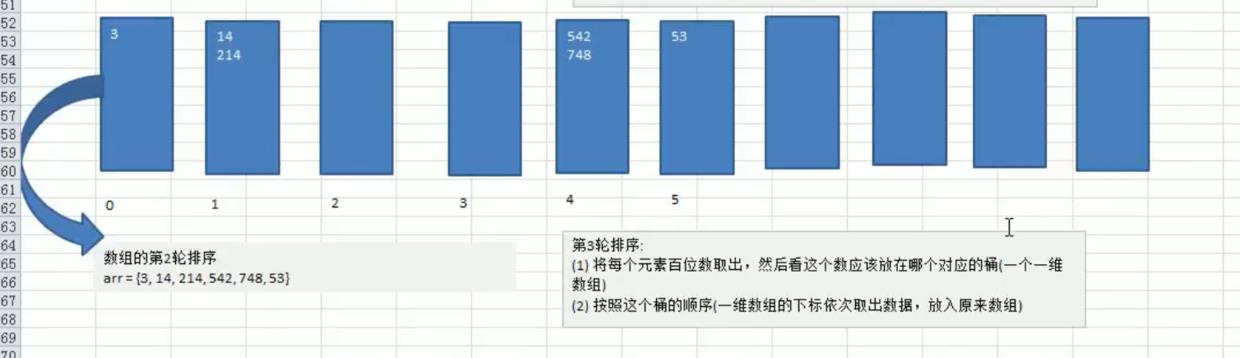

代码示例
/**
* 排序前:
* [833, 42, 5, 71, 1, 3, 6332, 28]
* 排序后:
* [1, 3, 5, 28, 42, 71, 833, 6332]
* 十万条数据排序耗时75(注意并不是开辟空间导致的耗时,而是桶排序的耗时比较大)
*/
public class RadixSort {
public static void main(String[] args) {
int[] array = {833, 42, 5, 71, 1, 3, 6332, 28};
System.out.println("排序前:");
System.out.println(Arrays.toString(array));
radixSort(array);
System.out.println("排序后:");
System.out.println(Arrays.toString(array));
int[] arrayTest = new int[10_0000];
for (int i = 0; i < 10_0000; i++) {
arrayTest[i] = (int) (Math.random() * 10_00000);
}
long start = System.currentTimeMillis();
radixSort(arrayTest);
// shellSortBySwap(arrayTest);//十万条数据排序耗时13043
long end = System.currentTimeMillis();
System.out.println("十万条数据排序耗时"+(end-start));
}
public static void radixSort(int[] array) {
//定义一个二维数组,表示10个桶,每个桶就是一个一维数组,每个一维数组大小为array.length,避免最坏情况数组溢出
//基数排序就是典型的空间换时间的算法
int[][] bucket = new int[10][array.length];
//记录每个桶中,实际存放了多少个数据,定义的一维数组下标对应每一个桶,值为数据个数
int[] bucketElementSize = new int[10];
//获取数组中最大的数
int maxNumber = array[0];
for (int i = 1; i < array.length; i++) {
if (array[i] > maxNumber) {
maxNumber = array[i];
}
}
//最大数字是几位数
int maxSize = String.valueOf(maxNumber).length();
int number = 0;
//针对每个元素对应的个十百千万位分别进行处理
for (int i = 0; i < maxSize; i++) {
for (int j = 0; j < array.length; j++) {
number = array[j] / (int) Math.pow(10, i) % 10;
bucket[number][bucketElementSize[number]] = array[j];
bucketElementSize[number] += 1;
}
//定义数组目前存放位置下标,从0到array.length
int index = 0;
//遍历每个桶,取出桶中的数据到原数组中
for (int m = 0; m < bucket.length; m++) {
//判断桶中有数据才进去遍历桶
if (bucketElementSize[m] > 0) {
for (int n = 0; n < bucketElementSize[m]; n++) {
//依次取出桶中元素到原数组,原数组下标index++后移一位
array[index++] = bucket[m][n];
}
//每轮遍历桶后都要对size置0,避免下一轮加入桶时size不等于0出错
bucketElementSize[m] =0;
}
}
}
}
}
扩展:关于排序的稳定性
稳定性和不稳定性的定义
通俗地讲就是能保证排序前两个相等的数其在序列的前后位置顺序和排序后它们两个的前后位置顺序相同。
稳定排序: 冒泡排序、插入排序、归并排序、基数排序
不稳定的排序: 选择排序、快速排序、希尔排序、堆排序
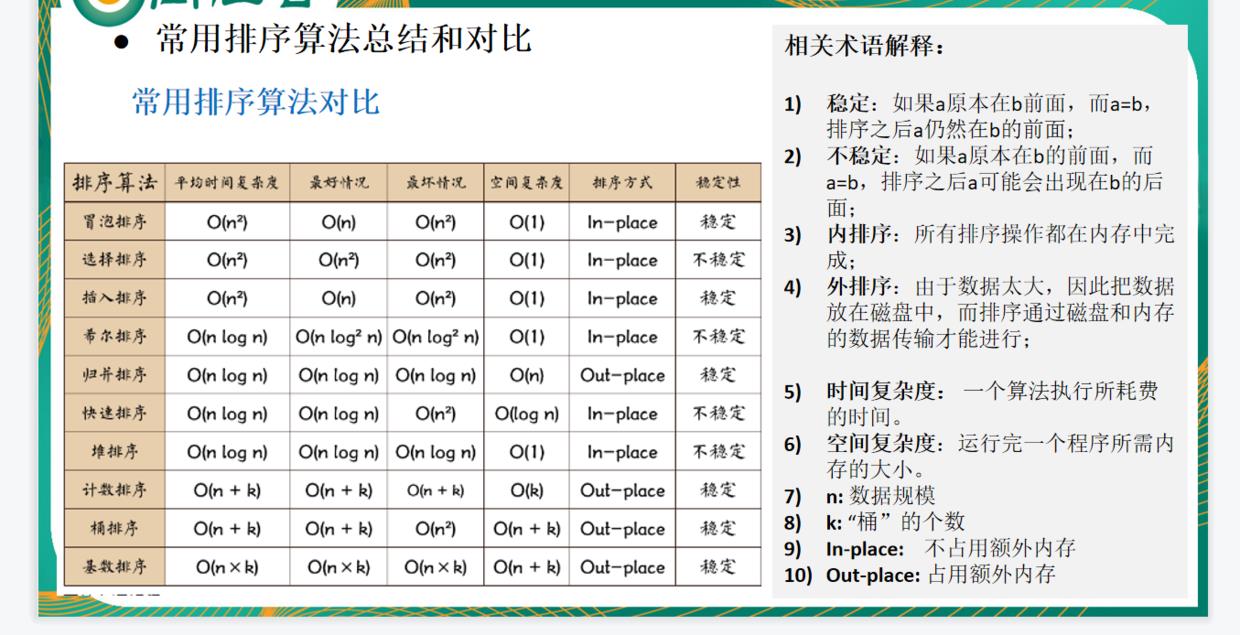
常用排序算法总结和对比
冒泡、选择、插入时间复杂度一般是O(n^2);
而希尔、归并、快速、堆排序的插入时间复杂度一般是O(n log n):线性对数阶;
而基数排序是O(n* k),因为k是桶的个数,因此,当排序数据较小时可以用基本的冒泡、选择、插入,而数据量上来后最后便是使用希尔、归并、快速、堆排序,但是当log n > k也就是桶的个数时,这时候应该选择基数排序,也就是说当数据量更加海量时选择基数排序。
查找算法
常用查找算法
- 顺序(线性)查找
- 二分查找/折半查找
- 插值查找
- 斐波那契查找
线性查找
前提:数组不需要有序
对数组进行从头到尾完全遍历一遍查找。
代码示例
public class SequenceSearch {
public static void main(String[] args) {
int[] array = {833, 42, 5, 71, 1, 3, 6332, 28};
int index = sequenceSearch(array, 3);
if (index != -1) {
System.out.println("找到了对应的数组下标为:"+index);
} else {
System.out.println("数组中找不到对应的元素");
}
//找到了对应的数组下标为:5
}
/**
* 顺序查找,返回第一个找到值的数组下标
* 如果要把所有下标都找出来则继续比对,并把找到的下标存放在集合中即可
* @param arr 数组
* @param value 查找值
* @return
*/
public static int sequenceSearch(int[] arr, int value) {
for (int i = 0; i < arr.length; i++) {
if (arr[i]== value) {
return i;
}
}
return -1;
}
}
二分查找
前提:数组有序
思路分析

代码示例——包含二分查找找出所有符合条件的下标集合
//使用二分查找的前提是该数组是有序的,如果无序则要先进行排序处理
/**
* 找到了对应的数组下标为:12
* [11,10,9,12,13,14,15,16]
*/
public class BinarySearch {
public static void main(String[] args) {
int[] array = {1, 2, 3, 4, 5, 6, 7,8, 9, 10, 10, 10, 10, 10 ,10, 10, 10,};
//注意右索引为array.length - 1
int index = binarySearch(array, 0, array.length - 1, 10);
if (index != -1) {
System.out.println("找到了对应的数组下标为:" + index);
} else {
System.out.println("数组中找不到对应的元素");
}
//查找所有符合条件的下标
List<Integer> list = binarySearchList(array, 0, array.length - 1, 10);
System.out.println(JSON.toJSONString(list));
}
/**
* 二分法查找,找到返回数组下标,找不到返回-1
*
* @param arr 数组
* @param left 左索引
* @param right 右索引
* @param value 要查找的值
* @return
*/
public static int binarySearch(int[] arr, int left, int right, int value) {
if (left > right) {
return -1;
}
// if (left < right) {
int mid = (left + right) / 2;
//要找的值比中间值大,向右递归
if (value > arr[mid]) {
//注意向右查找时mid下标对应的值不需要比对了,之间在mid + 1到right范围内查找,如果不加1则可能会导致栈溢出,
// 因为我们的判断条件是left < right,而此时因为找不到对应的值,得到的mid值会一直等于左索引或者右索引的一边,而mid一直没有变化,就会发生死归
return binarySearch(arr, mid + 1, right, value);
//要找的值比中间值小,向左递归
} else if (value < arr[mid]) {
return binarySearch(arr, left, mid - 1, value);
} else {
return mid;
}
// } else {
// return -1;
// }
}
/**
* 二分法查找
* 当一个有序数组中,有多个相同的数值时,如何将所有的数值都查找到,比如这里的 10.
* 思路:因为数组是有序的,当找到了要找的值时,以该值下标向左向右寻找是否还有相同的值即可
*
* @param arr 数组
* @param left 左索引
* @param right 右索引
* @param value 要查找的值
* @return
*/
public static List<Integer> binarySearchList(int[] arr, int left, int right, int value) {
if (left > right) {
return new ArrayList<>();
}
int mid = (left + right) / 2;
//要找的值比中间值大,向右递归
if (value > arr[mid]) {
//注意向右查找时mid下标对应的值不需要比对了,之间在mid + 1到right范围内查找,如果不加1则可能会导致栈溢出,
// 因为我们的判断条件是left < right,而此时因为找不到对应的值,得到的mid值会一直等于左索引或者右索引的一边,而mid一直没有变化,就会发生死归
return binarySearchList(arr, mid + 1, right, value);
//要找的值比中间值小,向左递归
} else if (value < arr[mid]) {
return binarySearchList(arr, left, mid - 1, value);
} else {
List<Integer> list = new ArrayList<>();
//注意 :这里不能用mid--给局部变量赋值,否则会导致mid也发生了变化
int tempIndex = mid - 1;
//向左查找
while (tempIndex >= 0 && arr[tempIndex] == value) {
list.add(tempIndex);
tempIndex--;
}
//添加mid
list.add(mid);
//向右查找
tempIndex = mid + 1;
//注意脚本不能越级的情况下判断是否相等,注意arr.length - 1是存在的,所有要用等于号
while (tempIndex <= arr.length - 1 && arr[tempIndex] == value) {
list.add(tempIndex);
tempIndex++;
}
return list;
}
}
}
插值查找
前提:数组有序
原理
插值查找算法类似于二分查找,不同的是插值查找每次从自适应mid处开始查找。将折半查找中的求mid 索引的公式 , low 表示左边索引left, high表示右边索引right.key 就是前面我们讲的 findVal。
int mid = low + (high - low) * (key - arr[low]) / (arr[high] - arr[low])
公式的意义:所预测的数字的位置占数组总长度的比例,可以理解为要寻找的值key到low的距离占整个区间的距离,值小靠左,值大靠右。

注意:这个要求数据尽量均匀分布。插值类似于平常查英文字典的方法,在查一个以字母C开头的英文单词时,决不会用二分查找,从字典的中间一页开始,因为知道它的大概位置是在字典的较前面的部分,因此可以从前面的某处查起,这就是插值查找的基本思想。
插值查找除要求查找表是顺序存储的有序表外,还要求数据元素的关键字在查找表中均匀分布,这样,就可以按比例插值。
思路分析

代码示例
插值查找注意事项
- 对于数据量较大,关键字分布比较均匀的查找表来说,采用插值查找, 速度较快.
- 关键字分布不均匀的情况下,该方法不一定比折半查找要好.
/**
* 测试插值次数
* 找到了对应的数组下标为:46
*/
public class InterpolationSearch {
public static void main(String[] args) {
int[] arr = new int[100];
//创建0到100的均匀有序数组
for (int i = 0; i < 100; i++) {
arr[i] = i + 1;
}
int index = interpolationSearch(arr, 0, arr.length - 1, 47);
if (index != -1) {
System.out.println("找到了对应的数组下标为:" + index);
} else {
System.out.println("数组中找不到对应的元素");
}
}
/**
* 前提是有序数组
* 插值查找,适合数据尽量均匀分布的有序数组
*
* @param arr 数组
* @param left 左索引
* @param right 右索引
* @param value 要查找的值
* @return 找到返回数组下标,找不到返回-1
*/
public static int interpolationSearch(int[] arr, int left, int right, int value) {
// 测试插值次数
System.out.println("测试插值次数");
//如果不在最初对要查找的值进行最大最小的比较排除,则因为要查找的值是会进公式计算出mid的,
// 计算结果会因为value值而无线膨胀或者缩小导致mid值失去意义,且会造成mid角标越级异常
//Exception in thread "main" java.lang.ArrayIndexOutOfBoundsException: 108 :这是用109测试时的结果
//value < arr[0] || value > arr[arr.length - 1] 必须需要
if (left > right || value < arr[0] || value > arr[arr.length - 1]) {
return -1;
}
int mid = left + (right - left) * (value - arr[left]) / (arr[right] - arr[left]);
//要找的值比中间值大,向右递归
if (value > arr[mid]) {
return interpolationSearch(arr, mid + 1, right, value);
//要找的值比中间值小,向左递归
} else if (value < arr[mid]) {
return interpolationSearch(arr, left, mid - 1, value);
} else {
return mid;
}
}
}
斐波那契查找——黄金分割法查找
基本介绍
黄金分割点是指把一条线段分割为两部分,使其中一部分与全长之比等于另一部分与这部分之比。取其前三位数字的近似值是0.618。由于按此比例设计的造型十分美丽,因此称为黄金分割,也称为中外比。这是一个神奇的数字,会带来意向不大的效果。
斐波那契数列 {1, 1, 2, 3, 5, 8, 13, 21, 34, 55 } 发现斐波那契数列的两个相邻数的比例,无限接近 黄金分割值0.618。
/**
* 斐波那契数列:返回第几位斐波那契数列的值
*
* @param number 第几位斐波那契数列
* @return
*/
public static long fibonacci(long number) {
if ((number == 0) || (number == 1)) {
return number;
} else {
return fibonacci(number - 1) + fibonacci(number - 2);
}
}
思路分析
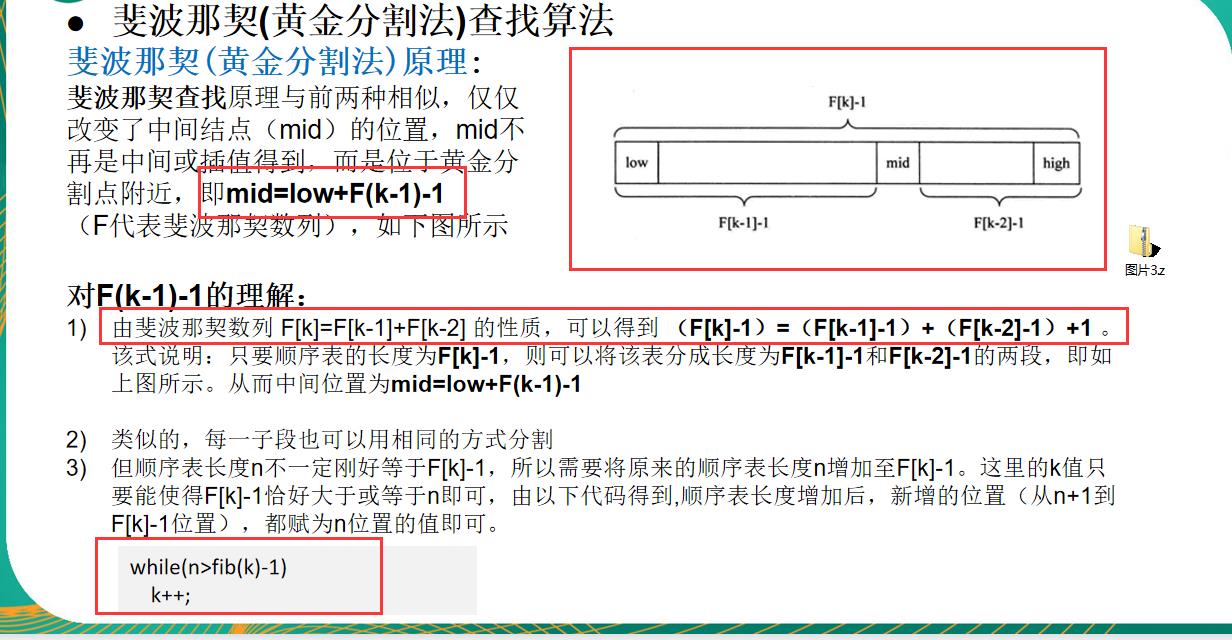
代码示例
//找到了对应的数组下标为:5
public class FibonacciSearch {
private static int maxSize = 20;
public static void main(String[] args) {
int[] array = {1, 8, 10, 89, 1000, 1234};
int index = fibonacciSearch(array, 1234);
if (index != -1) {
System.out.println("找到了对应的数组下标为:" + index);
} else {
System.out.println("数组中找不到对应的元素");
}
}
/**
* 斐波那契查找
*
* @param arr 数组
* @param value 查找值
* @return 返回数组下标,找不到返回-1
*/
public static int fibonacciSearch(int[] arr, int value) {
//因为mid = low + f[k - 1] - 1;所以要创建一个斐波那契数列返回第几位下斐波那契的值
//获取斐波那契数组
int[] f = createFibonacci();
//表示斐波那契分割数值对应的数组对应的下标
int k = 0;
int low = 0;
int high = arr.length - 1;
int mid = 0;
//这是其实是为了把查询数组分割成一个长度为8的线段,然后按照斐波那契的规律进行获取黄金分割点进行查找,
// 1,1,2,3,5,8从后往前就是各个位置的黄金分割点
//获取斐波那契数值对应的数组下标,这里的k=5,f[k]=8,因为我们的数组有6个数,所以斐波那契值刚好大于等于他的是8,
while (high > f[k] - 1) {
k++;
}
//将原查找表扩展为长度为F[n](如果要补充元素,则补充重复最后一个元素,直到满足F[n]个元素)
//补充最后一个元素是因为我们的数组是有序的,不能补充0,否则在比较是会出问题,补充最后一个元素刚好
//保证数组有序
int[] tempArr = Arrays.copyOf(arr, f[k]);
for (int j = high + 1; j < tempArr.length; j++) {
tempArr[j] = arr[high];
}
//low <= high 则可以继续寻找
while (low <= high) {
mid = low + f[k - 1] - 1;
//
if (value > tempArr[mid]) {
// k -= 2是因为 f[k]=f[k-1]+f[k-2],向右边则是查找f[k-2],则k-2
//这时候f[k-2] =f[k-3]+f[k-4]
k -= 2;
//向右查找则最低点变成mid + 1;
low = mid + 1;
//向数组的左边查找,把高位改为mid - 1
} else if (value < tempArr[mid]) {
// k -= 1是因为 f[k]=f[k-1]+f[k-2],向左边查找也就是查找f[k-1],则k-1;向右边则是查找f[k-2],则k-2
//这时候f[k-1] =f[k-2]+f[k-3]
k -= 1;
//向左查找则最高点变成mid -1;
high = mid - 1;
} else {
if (mid >= arr.length) {
return high;
} else {
return mid;
}
}
}
return -1;
}
//非递归方式斐波那契数组
private static int[] createFibonacci() {
int[] f = new int[maxSize];
f[0] = 1;
f[1] = 1;
for (int i = 2; i < f.length; i++) {
f[i] = f[i - 1] + f[i - 2];
}
return f;
}
private static int[] createFibonacci(int k) {
int[] f = new int[k];
f[0] = 1;
f[1] = 1;
for (int i = 2; i < f.length; i++) {
f[i] = f[i - 1] + f[i - 2];
}
return f;
}
/**
* 斐波那契数列:返回第几位斐波那契数列的值
*
* @param number 第几位斐波那契数列
* @return
*/
public static long fibonacci(long number) {
if ((number == 0) || (number == 1)) {
return number;
} else {
return fibonacci(number - 1) + fibonacci(number - 2);
}
}
}
哈希表——Hashtable——散列表
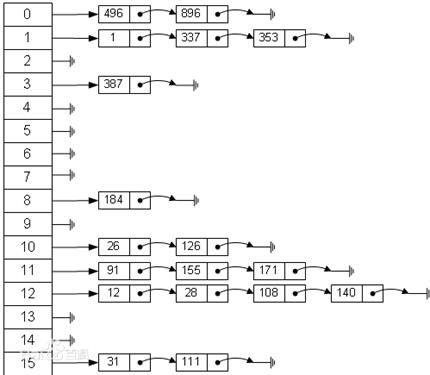
散列表(Hash table,也叫哈希表),是根据关键码值(Key value)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做散列表。
哈希表的结构示意图——数组+链表的结构(JDK1.8是数组+链表+红黑树)
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
手写一个hashmap?
代码示例
google公司的一个上机题:
有一个公司,当有新的员工来报道时,要求将该员工的信息加入(id,性别,年龄,名字,住址..),当输入该员工的id时,要求查找到该员工的所有信息.
要求:
不使用数据库,,速度越快越好=>哈希表(散列)
添加时,保证按照id从低到高插入 [课后思考:如果id不是从低到高插入,但要求各条链表仍是从低到高,怎么解决?]
使用链表来实现哈希表, 该链表不带表头[即: 链表的第一个结点就存放雇员信息]
思路分析并画出示意图
代码实现[增删改查(显示所有员工,按id查询)]
public class HashTable<E> {
private SingleLinkedList<E>[] singleLinkedListArr;
private int size;
public HashTable(int size) {
this.size = size;
this.singleLinkedListArr = new SingleLinkedList[size];
for (int i = 0; i < this.singleLinkedListArr.length; i++) {
singleLinkedListArr[i] = new SingleLinkedList();
}
}
public void add(E e) {
singleLinkedListArr[hash(e)].add(e);
}
public void list() {
for (int i = 0; i < singleLinkedListArr.length; i++) {
if (singleLinkedListArr[i].getSize() > 0) {
singleLinkedListArr[i].list();
}
}
}
public E findById(int id) {
return singleLinkedListArr[id%size].findById(id);
}
private int hash(E e) {
if (e instanceof Employee) {
Employee employee = (Employee) e;
return employee.getId() % size;
} else {
return e.hashCode() % size;
}
}
}
public class SingleLinkedList<E> {
//head指向第一个元素,没有专门的head头结点
private Node<E> head;
private int size;
public int getSize() {
return size;
}
public void add(E e) {
if (head == null) {
head = new Node<E>(e);
size++;
} else {
Node<E> temp = head;
while (temp.next != null) {
temp = temp.next;
}
Node<E> node = new Node<E>(e);
temp.next = node;
size++;
}
}
public void list() {
if (head == null) {
return;
} else {
Node<E> temp = head;
while (temp != null) {
System.out.printf("%s\\t", temp.getE());
temp = temp.next;
}
System.out.println();
}
}
public E findById(int id) {
boolean flag = false;
Node<E> temp = this.head;
while (temp != null) {
if (temp.getE() instanceof Employee) {
Employee employee = (Employee) temp.getE();
if (employee.getId() == id) {
flag = true;
break;
}
}
temp = temp.next;
}
if (flag) {
return temp.getE();
}
return null;
}
public void delete(E e) {
if (head == null) {
return;
} else {
boolean flag = false;
Node<E> temp = head.next;
while (temp.next != null) {
if (temp.next.getE().equals(e)) {
flag = true;
break;
}
temp = temp.next;
}
if (flag) {
temp.next = temp.next.next;
}
}
}
private static class Node<E> {
private E e;
private Node<E> next;
public E getE() {
return e;
}
public Node<E> getNext() {
return next;
}
public Node(E e) {
this.e = e;
}
@Override
public String toString() {
return "Node{" +
"e=" + e +
\'}\';
}
}
}
public class Employee {
private Integer id;
private String name;
public Employee() {
}
public Employee(Integer id,String name){
this.id = id;
this.name =name;
}
public Integer getId() {
return id;
}
public void setId(Integer id) {
this.id = id;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
@Override
public String toString() {
return "Employee{" +
"id=" + id +
", name=\'" + name + \'\\\'\' +
\'}\';
}
}
public class HashTableTest {
public static void main(String[] args) {
HashTable<Employee> hashTable = new HashTable<Employee>(10);
hashTable.add(new Employee(1,"小强"));
hashTable.add(new Employee(2,"艾米"));
hashTable.add(new Employee(12,"艾米"));
hashTable.list();
System.out.printf("查找%d的元素的值%s",12,hashTable.findById(12));
System.out.println();
System.out.printf("查找%d的元素的值%s",13,hashTable.findById(13));
}
/**
* Employee{id=1, name=\'小强\'}
* Employee{id=2, name=\'艾米\'} Employee{id=12, name=\'艾米\'}
* 查找12的元素的值Employee{id=12, name=\'艾米\'}
* 查找13的元素的值null
*/
}
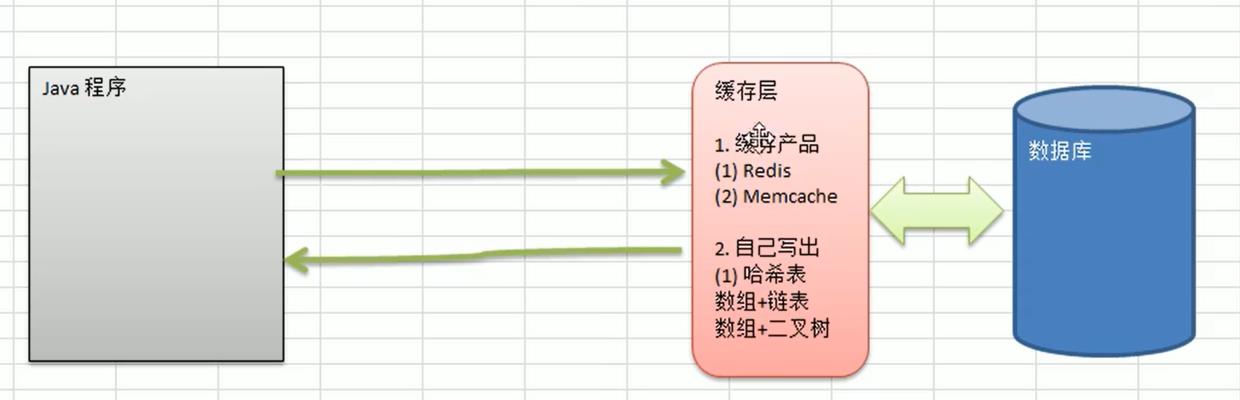
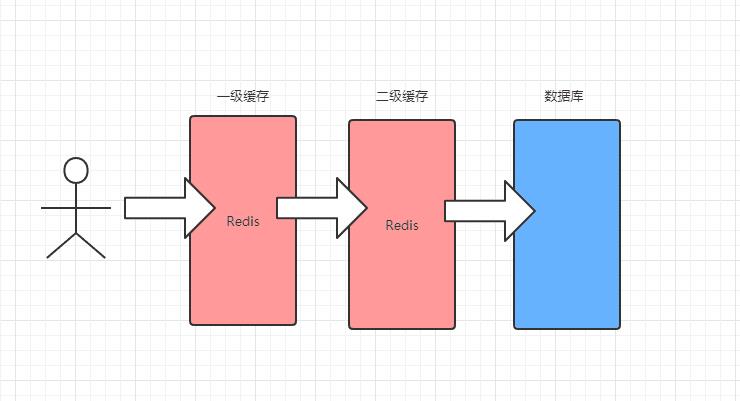
扩展:有了一级缓存,为什么还要二级缓存?
一级缓存不够就可以再加一级缓存,变成二级缓存。二级缓存的作用又是什么呢?简单地说,二级缓存就是一级缓存的缓冲器:一级缓存制造成本很高因此它的容量有限,二级缓存的作用就是存储那些CPU处理时需要用到、一级缓存又无法存储的数据。同样道理,三级缓存和内存可以看作是二级缓存的缓冲器,它们的容量递增,但单位制造成本却递减。需要注意的是,无论是二级缓存、三级缓存还是内存都不能存储处理器操作的原始指令,这些指令只能存储在CPU的一级指令缓存中,而余下的二级缓存、三级缓存和内存仅用于存储CPU所需数据。
树
为什么需要树这种数据结构
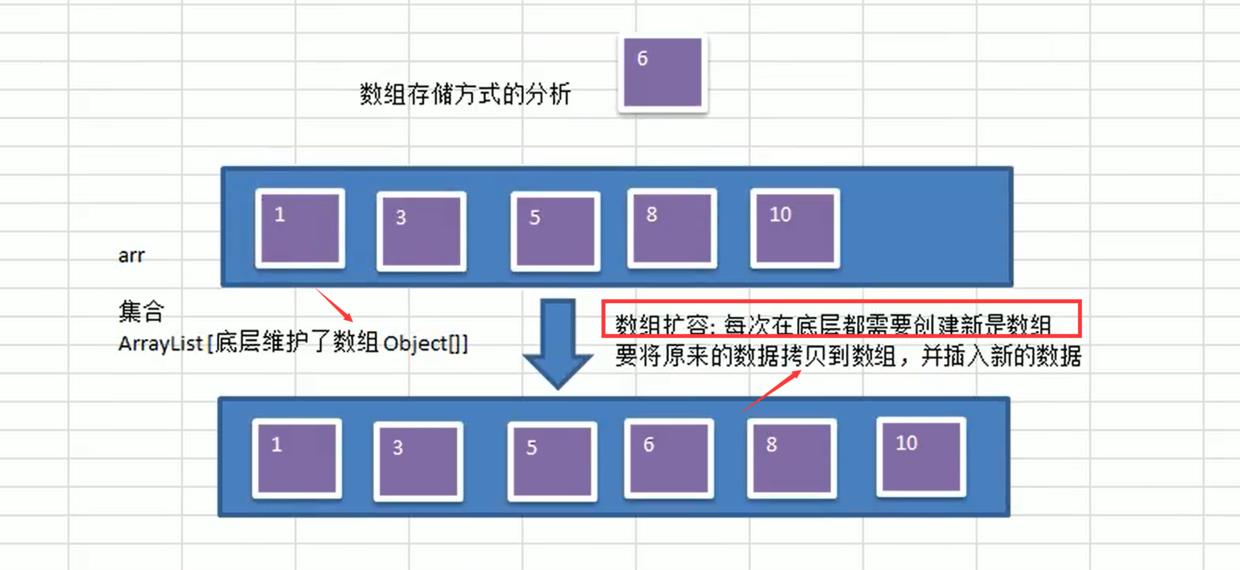
- 数组存储方式的分析——查找快,增删慢
优点:通过下标方式访问元素,速度快。对于有序数组,还可使用二分查找提高检索速度。
缺点:如果要检索具体某个值,或者插入值(按一定顺序)会整体移动,效率较低 。
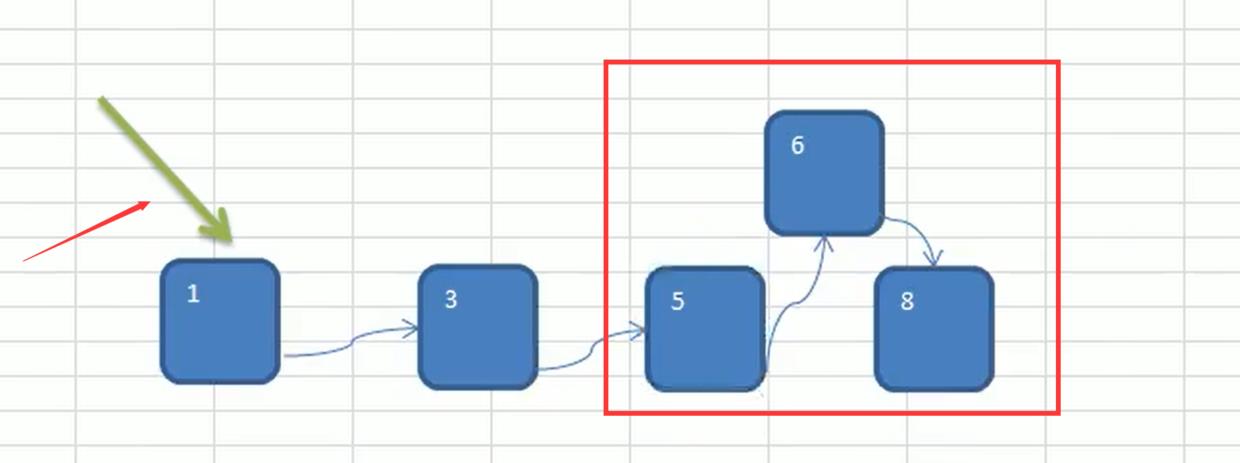
- 链式存储方式的分析——查找慢,增删快
优点:在一定程度上对数组存储方式有优化(比如:插入一个数值节点,只需要将插入节点,链接到链表中即可, 删除效率也很好)。
缺点:在进行检索时,效率仍然较低,比如(检索某个值,需要从头节点开始遍历)
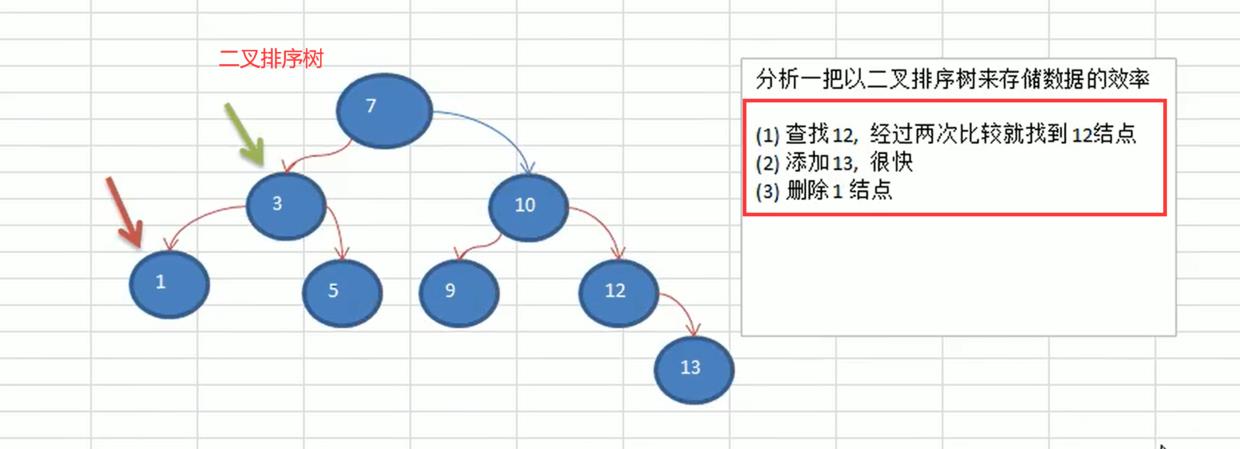
- 树存储方式的分析——查找增删都相对较快
能提高数据存储,读取的效率, 比如利用二叉排序树(Binary Sort Tree),既可以保证数据的检索速度,同时也可以保证数据的插入,删除,修改的速度。
扩展
ArrayList底层扩容说明

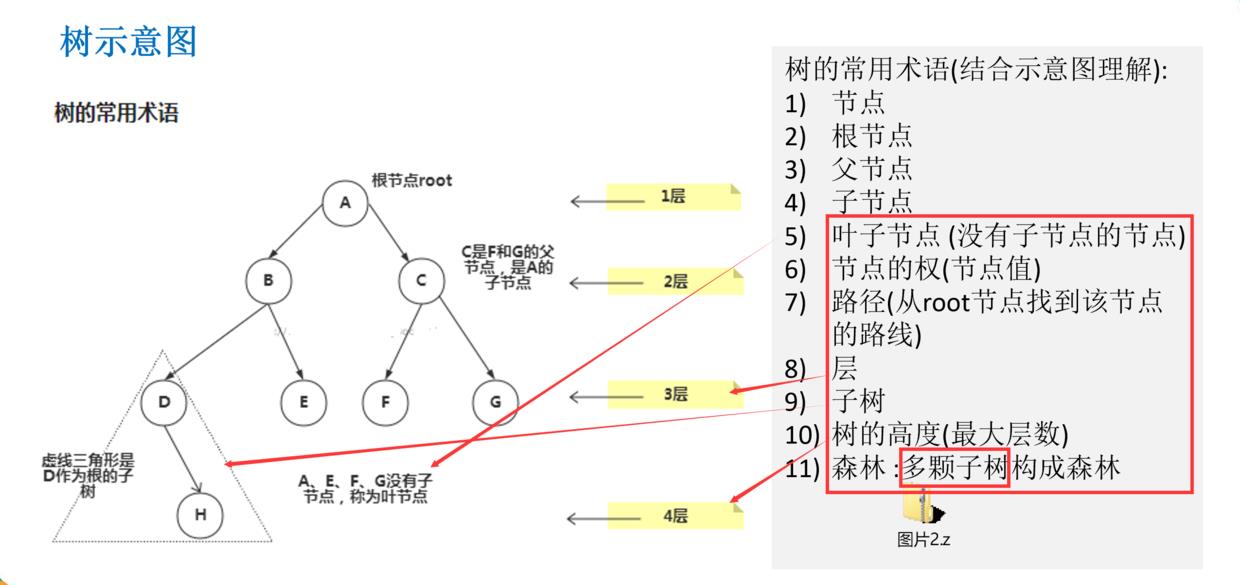
树的常用术语
二叉树简介
-
树有很多种,每个节点最多只能有两个子节点的一种形式称为二叉树。
-
二叉树的子节点分为左节点和右节点。
-
只有左节点或者只有右节点也是一个二叉树。
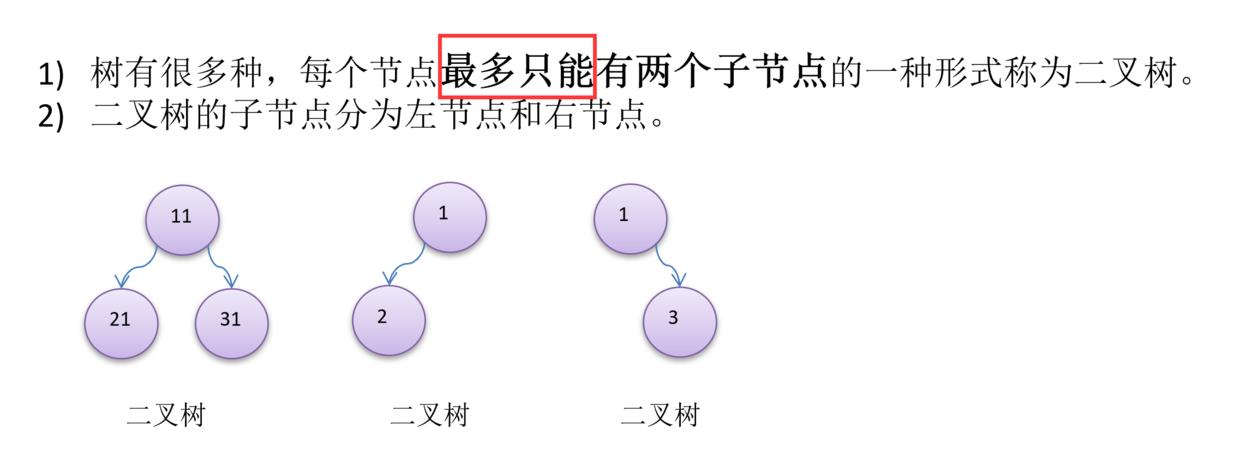
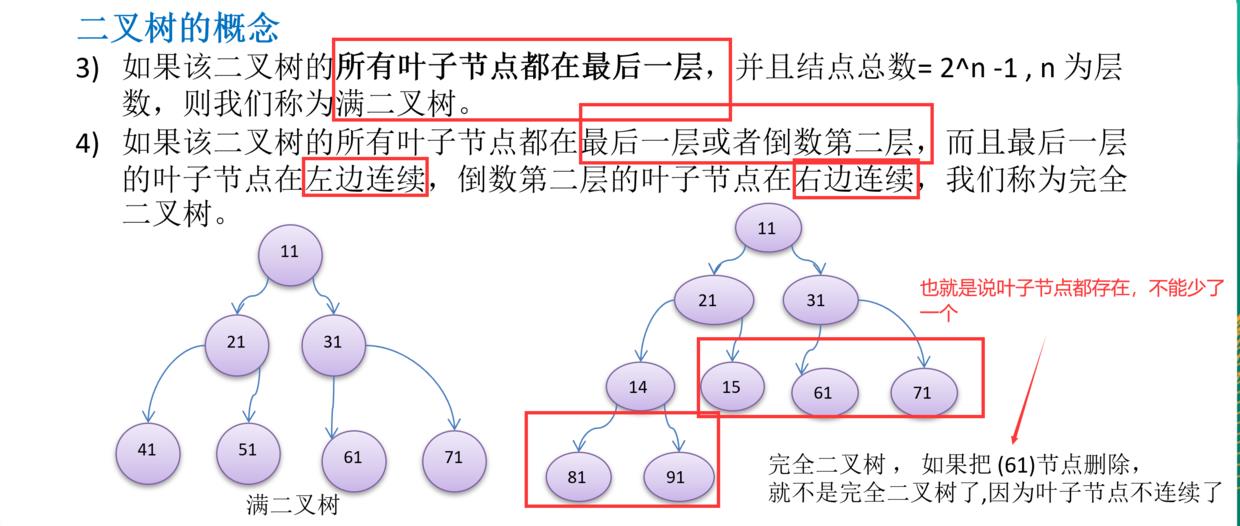
满二叉树和完全二叉树
满二叉树节点总数=2^n -1,满二叉树是特殊的完全二叉树。
二叉树的遍历
二叉树的遍历有前序、中序、后续遍历三种方式。
前序遍历: 先输出父节点,再遍历左子树和右子树
中序遍历: 先遍历左子树,再输出父节点,再遍历右子树
后序遍历: 先遍历左子树,再遍历右子树,最后输出父节点
小结: 看输出父节点的顺序,就确定是前序,中序还是后序
前序遍历—— Preorder Traversal
前序遍历(VLR), 是二叉树遍历的一种,也叫做先根遍历、先序遍历、前序周游,可记做根左右。前序遍历首先访问根结点然后遍历左子树,最后遍历右子树。
中序遍历——Inorder Traversal
中序遍历(LDR)是二叉树遍历的一种,也叫做中根遍历、中序周游。在二叉树中,中序遍历首先遍历左子树,然后访问根结点,最后遍历右子树。
后序遍历——Postorder Traversal
后序遍历(LRD)是二叉树遍历的一种,也叫做后根遍历、后序周游,可记做左右根。后序遍历有递归算法和非递归算法两种。在二叉树中,先左后右再根,即首先遍历左子树,然后遍历右子树,最后访问根结点。
树的遍历思路分析
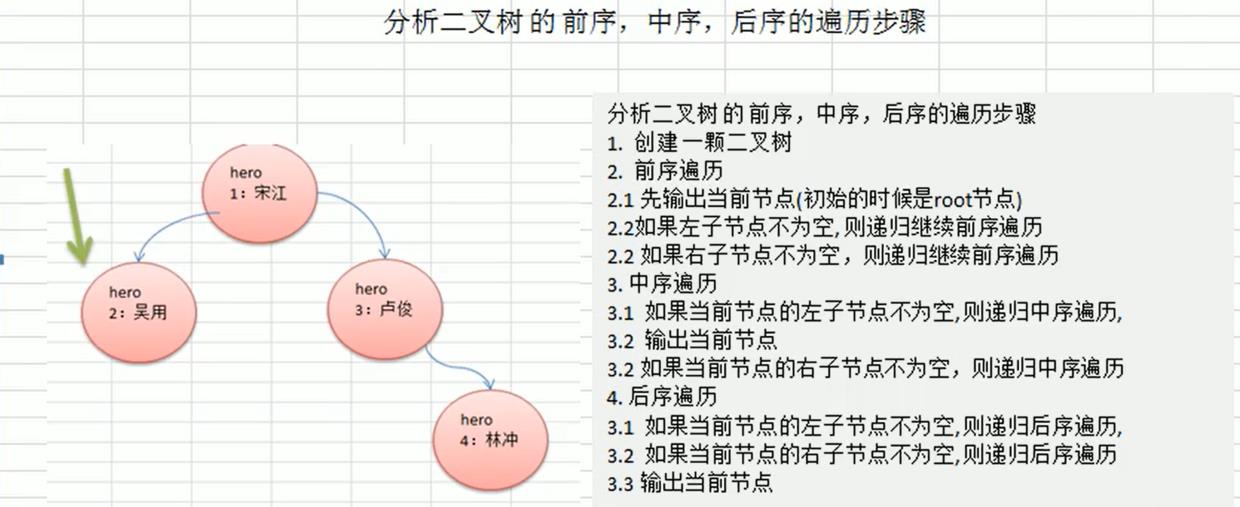
代码示例——前序、中序、后续遍历
public class BinaryTree<E> {
private TreeNode<E> root;
//前序
public void preOrder(){
if (this.root != null) {
this.root.preOrder();
}
}
//中序
public void inOrder(){
if (this.root != null) {
this.root.inOrder();
}
}
//后序
public void postOrder(){
if (this.root != null) {
this.root.postOrder();
}
}
public BinaryTree(TreeNode<E> root) {
this.root = root;
}
public TreeNode<E> getRoot() {
return root;
}
public void setRoot(TreeNode<E> root) {
this.root = root;
}
public static class TreeNode<E> {
private E item;
private TreeNode<E> left;
private TreeNode<E> right;
public TreeNode(E item) {
this.item = item;
}
/**
* 前序遍历
*/
public void preOrder() {
System.out.println(this.getItem());
//递归向左子树前序遍历
if (this.getLeft() != null) {
this.getLeft().preOrder();
}
//递归向右子树前序遍历
if (this.getRight() != null) {
this.getRight().preOrder();
}
}
/**
* 中序遍历
*/
public void inOrder() {
//递归向左子树中序遍历
if (this.getLeft() != null) {
this.getLeft().inOrder();
}
System.out.println(this.getItem());
//递归向右子树中序遍历
if (this.getRight() != null) {
this.getRight().inOrder();
}
}
public void postOrder() {
//递归向左子树后序遍历
if (this.getLeft() != null) {
this.getLeft().postOrder();
}
//递归向右子树后序遍历
if (this.getRight() != null) {
this.getRight().postOrder();
}
System.out.println(this.getItem());
}
public E getItem() {
return item;
}
public void setItem(E item) {
this.item = item;
}
public TreeNode<E> getLeft() {
return left;
}
public void setLeft(TreeNode<E> left) {
this.left = left;
}
public TreeNode<E> getRight() {
return right;
}
public void setRight(TreeNode<E> right) {
this.right = right;
}
}
}
public class Hero {
private Integer id;
private String name;
public Hero(Integer id, String name) {
this.id = id;
this.name = name;
}
@Override
public String toString() {
return "Hero{" +
"id=" + id +
", name=\'" + name + \'\\\'\' +
\'}\';
}
}
/**
* --------------前序------------------
* Hero{id=1, name=\'艾米哈珀\'}
* Hero{id=2, name=\'大青山\'}
* Hero{id=3, name=\'霍恩斯\'}
* Hero{id=5, name=\'绿儿\'}
* Hero{id=4, name=\'池傲天\'}
* --------------中序------------------
* Hero{id=2, name=\'大青山\'}
* Hero{id=1, name=\'艾米哈珀\'}
* Hero{id=5, name=\'绿儿\'}
* Hero{id=3, name=\'霍恩斯\'}
* Hero{id=4, name=\'池傲天\'}
* --------------后序------------------
* Hero{id=2, name=\'大青山\'}
* Hero{id=5, name=\'绿儿\'}
* Hero{id=4, name=\'池傲天\'}
* Hero{id=3, name=\'霍恩斯\'}
* Hero{id=1, name=\'艾米哈珀\'}
*/
public class BinaryTreeTest {
public static void main(String[] args) {
BinaryTree tree = createBinaryTree();
System.out.println("--------------前序------------------");
tree.preOrder();
System.out.println("--------------中序------------------");
tree.inOrder();
System.out.println("--------------后序------------------");
tree.postOrder();
}
public static BinaryTree createBinaryTree(){
BinaryTree.TreeNode<Hero> root = new BinaryTree.TreeNode<>(new Hero(1, "艾米哈珀"));
BinaryTree.TreeNode<Hero> node2 = new BinaryTree.TreeNode<>(new Hero(2, "大青山"));
BinaryTree.TreeNode<Hero> node3 = new BinaryTree.TreeNode<>(new Hero(3, "霍恩斯"));
BinaryTree.TreeNode<Hero> node4 = new BinaryTree.TreeNode<>(new Hero(4, "池傲天"));
BinaryTree.TreeNode<Hero> node5 = new BinaryTree.TreeNode<>(new Hero(5, "绿儿"));
root.setLeft(node2);
root.setRight(node3);
node3.setRight(node4);
node3.setLeft(node5);
BinaryTree<Hero> tree = new BinaryTree<>(root);
tree.setRoot(root);
return tree;
}
}
二叉树查找——通过前序、中序、后序查找
思路分析
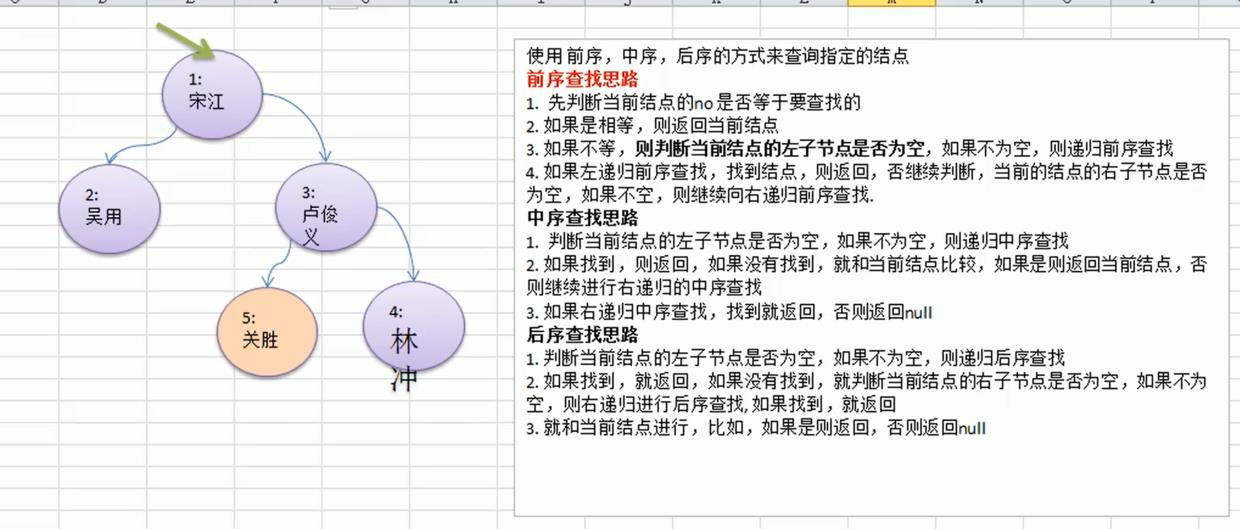
二叉树删除
删除要通过判断当前节点的子节点是否为要删除的对象来进行删除,,因为树的当前节点没有保存父节点的信息,是单向的,跟单向链表要找被删除节点的前一个节点一样。
思路分析
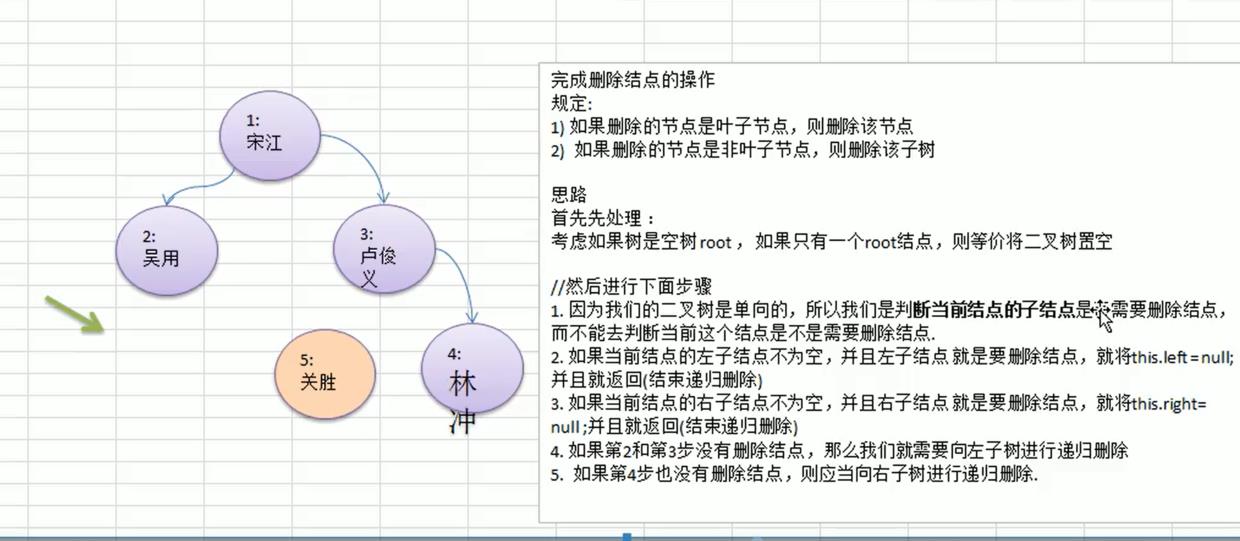
二叉树查找和删除代码示例
public class BinaryTree {
private HeroNode root;
public BinaryTree(HeroNode root) {
this.root = root;
}
public HeroNode getRoot() {
return root;
}
public void setRoot(HeroNode root) {
this.root = root;
}
/**
* 二叉树删除
* 如果删除的节点是叶子节点,则删除该节点
* 如果删除的节点是非叶子节点,则删除该子树
* @param id
*/
public void delete(Integer id) {
//先判断节点是否为空
if (root == null) {
System.out.println("根节点为空,无法删除");
return;
}
//第一步先判断根节点是否为要删除的节点
if (Objects.equals(root.getId(),id)) {
this.setRoot(null);
return;
}
//递归判断删除
this.root.deleteNode(id);
}
//前序
public void preOrder() {
if (this.root != null) {
this.root.preOrder();
}
}
//中序
public void inOrder() {
if (this.root != null) {
this.root.inOrder();
}
}
//后序
public void postOrder() {
if (this.root != null) {
this.root.postOrder();
}
}
//前序
public HeroNode preOrderSearch(Integer id) {
if (this.root != null) {
return this.root.preOrderSearch(id);
}
return null;
}
//中序
public HeroNode inOrderSearch(Integer id) {
if (this.root != null) {
return this.root.inOrderSearch(id);
}
return null;
}
//后序
public HeroNode postOrderSearch(Integer id) {
if (this.root != null) {
return root.postOrderSearch(id);
}
return null;
}
public static class HeroNode {
private Integer id;
private String name;
private HeroNode left;
private HeroNode right;
public HeroNode(Integer id, String name) {
this.id = id;
this.name = name;
}
public Integer getId() {
return id;
}
public void setId(Integer id) {
this.id = id;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
/**
* 递归删除节点
* 删除要通过判断当前节点的子节点是否为要删除的对象来进行删除,
* 因为树的当前节点没有保存父节点的信息,是单向的,跟单向链表要找被删除节点的前一个节点一样。
*/
public void deleteNode(Integer id) {
//这边是按照一直往左比较递归的思路写的,如果要按照树的结构来进行删除的话
//就要在判断左节点不相等后判断右节点是否相等,只有两个都不相等时,
//才能向左递归删除,再向右递归删除
if (this.left != null) {
if (Objects.equals(this.left.id,id)) {
this.left = null;
return;
} else {
this.left.deleteNode(id);
}
}
if (this.right != null) {
if (Objects.equals(this.right.id,id)) {
this.right = null;
return;
} else {
this.right.deleteNode(id);
}
}
}
/**
* 前序查找
*/
public HeroNode preOrderSearch(Integer id) {
if (Objects.equals(this.id, id)) {
return this;
}
HeroNode node = null;
if (this.left != null) {
node = this.left.preOrderSearch(id);
}
if (node == null && this.right != null) {
node = this.right.preOrderSearch(id);
}
return node;
}
/**
* 中序查找
*/
public HeroNode inOrderSearch(Integer id) {
HeroNode node = null;
if (this.left != null) {
node = this.left.inOrderSearch(id);
}
if (node == null && Objects.equals(this.id, id)) {
return this;
}
if (node == null && this.right != null) {
node = this.right.inOrderSearch(id);
}
return node;
}
/**
* 后序查找
*/
public HeroNode postOrderSearch(Integer id) {
HeroNode node = null;
if (this.left != null) {
node = this.left.postOrderSearch(id);
}
if (node == null && this.right != null) {
node = this.right.postOrderSearch(id);
}
if (node == null && Objects.equals(this.id, id)) {
node = this;
}
return node;
}
/**
* 前序遍历
*/
public void preOrder() {
System.out.println(this);
//递归向左子树前序遍历
if (this.getLeft() != null) {
this.getLeft().preOrder();
}
//递归向右子树前序遍历
if (this.getRight() != null) {
this.getRight().preOrder();
}
}
/**
* 中序遍历
*/
public void inOrder() {
//递归向左子树中序遍历
if (this.getLeft() != null) {
this.getLeft().inOrder();
}
System.out.println(this);
//递归向右子树中序遍历
if (this.getRight() != null) {
this.getRight().inOrder();
}
}
public void postOrder() {
//递归向左子树后序遍历
if (this.getLeft() != null) {
this.getLeft().postOrder();
}
//递归向右子树后序遍历
if (this.getRight() != null) {
this.getRight().postOrder();
}
System.out.println(this);
}
@Override
public String toString() {
return "HeroNode{" +
"id=" + id +
", name=\'" + name + \'\\\'\' +
\'}\';
}
}
}
/**
* --------------前序------------------
* HeroNode{id=1, name=\'艾米哈珀\'}
* HeroNode{id=2, name=\'大青山\'}
* HeroNode{id=3, name=\'霍恩斯\'}
* HeroNode{id=5, name=\'绿儿\'}
* HeroNode{id=4, name=\'池傲天\'}
* --------------中序------------------
* HeroNode{id=2, name=\'大青山\'}
* HeroNode{id=1, name=\'艾米哈珀\'}
* HeroNode{id=5, name=\'绿儿\'}
* HeroNode{id=3, name=\'霍恩斯\'}
* HeroNode{id=4, name=\'池傲天\'}
* --------------后序------------------
* HeroNode{id=2, name=\'大青山\'}
* HeroNode{id=5, name=\'绿儿\'}
* HeroNode{id=4, name=\'池傲天\'}
* HeroNode{id=3, name=\'霍恩斯\'}
* HeroNode{id=1, name=\'艾米哈珀\'}
* --------------前序查找------------------
* 前序查找:HeroNode{id=5, name=\'绿儿\'}
* --------------中序查找------------------
* 中序查找:HeroNode{id=5, name=\'绿儿\'}
* --------------后序查找------------------
* 后序查找:HeroNode{id=5, name=\'绿儿\'}
* 后序查找:null
* --------------删除节点5------------------
* --------------删除后前序遍历------------------
* HeroNode{id=1, name=\'艾米哈珀\'}
* HeroNode{id=2, name=\'大青山\'}
* HeroNode{id=3, name=\'霍恩斯\'}
* HeroNode{id=4, name=\'池傲天\'}
*
* Process finished with exit code 0
*/
public class BinaryTreeTest {
public static void main(String[] args) {
BinaryTree tree = createBinaryTree();
System.out.println("--------------前序------------------");
tree.preOrder();
System.out.println("--------------中序------------------");
tree.inOrder();
System.out.println("--------------后序------------------");
tree.postOrder();
System.out.println("--------------前序查找------------------");
System.out.println("前序查找:" + tree.preOrderSearch(5));
System.out.println("--------------中序查找------------------");
System.out.println("中序查找:" + tree.inOrderSearch(5));
System.out.println("--------------后序查找------------------");
System.out.println("后序查找:" + tree.postOrderSearch(5));
System.out.println("后序查找:"+tree.postOrderSearch(20));
System.out.println("--------------删除节点5------------------");
tree.delete(5);
System.out.println("--------------删除后前序遍历------------------");
tree.preOrder();
}
public static BinaryTree createBinaryTree() {
BinaryTree.HeroNode root = new BinaryTree.HeroNode(1, "艾米哈珀");
BinaryTree.HeroNode node2 = new BinaryTree.HeroNode(2, "大青山");
BinaryTree.HeroNode node3 = new BinaryTree.HeroNode(3, "霍恩斯");
BinaryTree.HeroNode node4 = new BinaryTree.HeroNode(4, "池傲天");
BinaryTree.HeroNode node5 = new BinaryTree.HeroNode(5, "绿儿");
root.setLeft(node2);
root.setRight(node3);
node3.setRight(node4);
nod以上是关于数据结构与算法——基础篇的主要内容,如果未能解决你的问题,请参考以下文章