图

Posted 2021-05-29 亿杯奶茶

图的思维导图

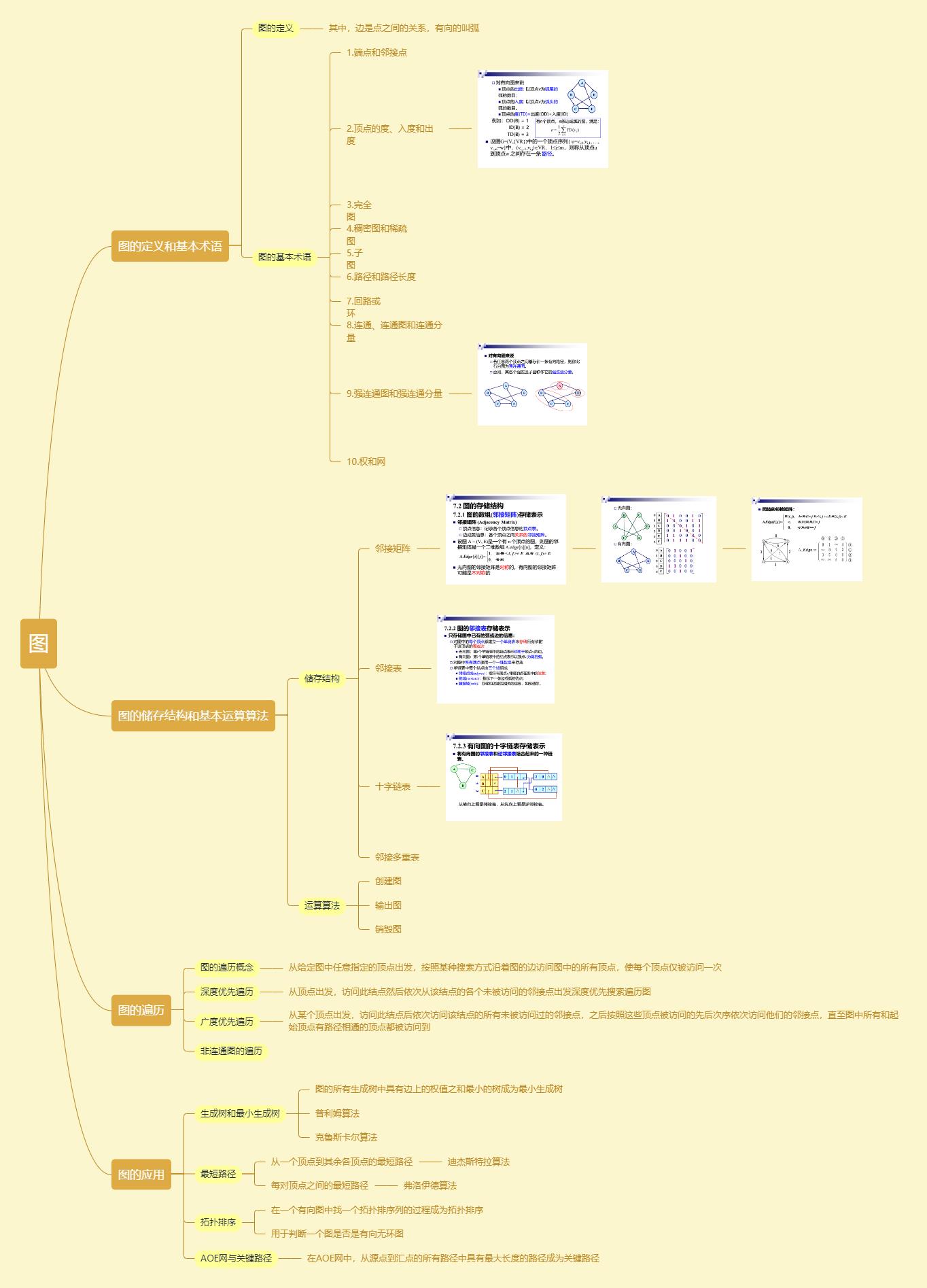
图的重要概念丰富

图的储存结构和基本运算算法

（一）邻接矩阵储存法

• 图的完整邻接矩阵类型声明：

  #define MAXV<最大顶点个数>
  #define INF 32767           //定义∞ 
  typedef struct
  { int no;                   //顶点的编号
    Info Type info;           //顶点的其他信息      
  }Vertex Type;               //顶点的类型
  typedef struct
  {  int edges[MAXV][MAXV];   //邻接矩阵数组
     int n e;                 //顶点数，边数
     VertexType vexs[MAXV];   //存放顶点信息
  }MatGraph;                  //完整的图邻接矩阵类型

（二）邻接表储存法

• 图的完整邻接表储存类型声明如下：

  typedef struct ANode
{ int adjvex;               //该边的邻接点编号
  struct ANode *nextarc;    //指向下一条边的指针
  int weight;               //该边的相关信息
}ArcNode;                   //边结点的类型
typedef struct Vnode
{  Info Type info;
   ArcNode *firstarc;
}VNode;
typedef struct
{ VNode adjlist[MAXV];      //邻接表的头结点数组
  int n,e;                  //图中的顶点数n和边数e
}AdjGraph;                  //完整的图邻接表类型

（三）图的运算算法

• 图的运算包括创建图、输出图及销毁图
  创建图根据邻接矩阵数组A、顶点个数n和边数e来建立图的邻接表G。输出图通过扫描邻接表G的头结点再对于每个单链表输出头结点的顶点信息，然后逐一输出单链表中的所有结点的顶点编号。销毁图对于邻接表G，扫描其头结点数组指向的所有单链表，逐个释放单链表中的边结点，最后释放头结点数组。

---

---

图的遍历

• 深度优先遍历算法如下：

  int visited[MAX]={0};         //全局数组
  void DFS(AdjGraph *G,int v)   //深度优先遍历算法
  {
    ArcNode *p;
    visited[v]=1;               //置已访问标记
    printf("%d",v);             //输出被访问顶点的编号
    p=G->adjlist[v].firstarc;   //p指向顶点v的第一个邻接点
    while(p!=NULL)
    {
       if(visited[p->adjvex]==0) //若p->adjvex顶点未被访问，递归访问它
         DFS(G,p->adjvex);
       p=p->nextarc;             //p指向顶点v的下一个邻接点
     }
  }

• 广度优先遍历
  广度优先遍历以邻接表为储存结构，在用广度优先遍历图时需要使用一个队列，可采用环形队列，以类似于二叉树的层次遍历方式来遍历图。在此暂不列出算法。
• DFS与BFS算法效率比较：
  1、二者空间复杂度相同，都为O(n)(都使用了堆栈或队列）
  2、时间复杂度只与储存结构（邻接矩阵和邻接表）有关，而与搜索路径无关。
  3、搜索路径由储存结构与算法共同决定

---

图的应用

• 生成树与最小生成树
  
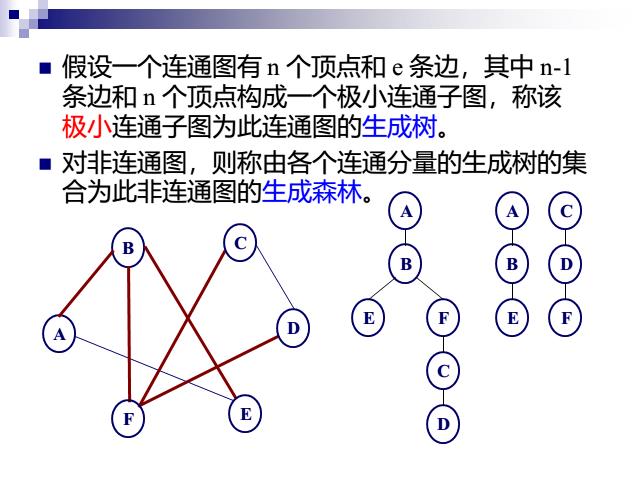
  其中：图的所有生成树中具有边上的权值之和最小的树成为最小生成树

• 最短路径
  
  Dijkstra算法：
  

• 拓扑排序
  （1）从一个有向图中选择一个没有前驱的顶点并输出它。
  （2）从图中删去该顶点，并删去从该顶点发出的全部有向边。
  （3）重复（1）（2）两步、直到剩余的图中不再存在没有前驱的顶点为止。

• AOE网与关键路径
  在AOE网中，从源点到汇点的所有路径中具有最大长度的路径成为关键路径。
  

尚存问题：
对于图应用方面掌握不足