1064. 小国王(状压DP&棋盘式)

Posted 2021-05-27 Are~you~ready

题目：https://www.acwing.com/problem/content/1066/

在 n×n 的棋盘上放 k 个国王，国王可攻击相邻的 8 个格子，求使它们无法互相攻击的方案总数。
输入格式
共一行，包含两个整数 n 和 k。
输出格式
共一行，表示方案总数，若不能够放置则输出0。
数据范围
1≤n≤10,
0≤k≤n2

题解：状压DP，第i行只与第i-1行有关系，每一行的所有方案都可以用一个二进制状态来表示，1表示放置了国王，0表示没有，，f[n][m][k],第一维是棋盘n，第二维是放了几个国王，第三维表示的是二进制状态。

y总讲解：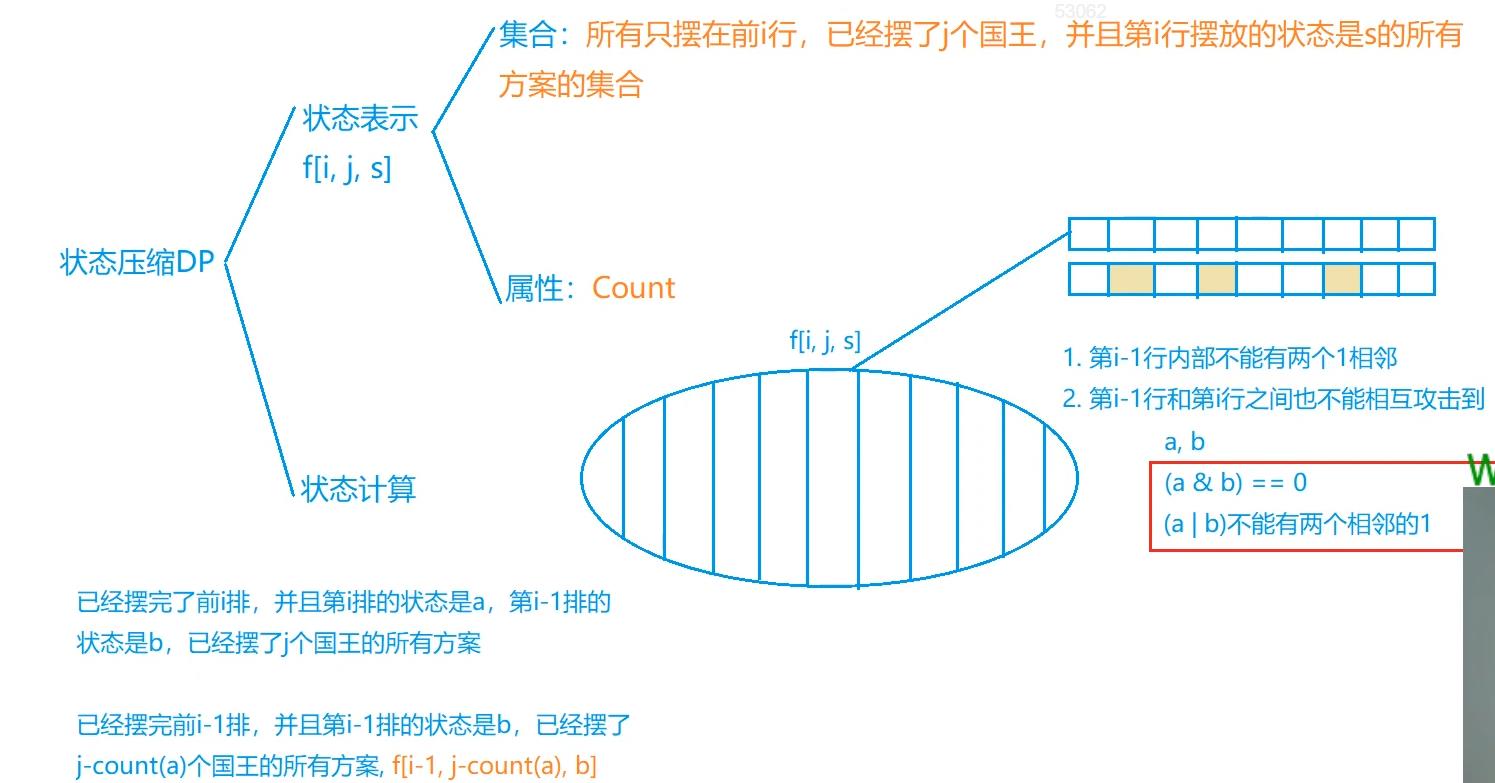

 

 

#include <algorithm>
#include <bitset>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <deque>
#include <functional>
#include <iostream>
#include <map>
#include <queue>
#include <set>
#include <stack>
#include <string>
#include <vector>
//#include <unordered_map>
//#include <unordered_set>
//#include <bits/stdc++.h>
//#define int long long
#define pb push_back
#define PII pair<int, int>
#define mpr make_pair
#define ms(a, b) memset((a), (b), sizeof(a))
#define x first
#define y second
typedef long long ll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int N = 12, M = 1 << 10, K = 110;
using namespace std;

vector<int> vec,
    h[M];  // vec存所有可以用的状态，h存每一个状态能够从哪个状态转移过来
int cnt[M];  //存每个状态包涵1的数量，即这个状态用了几个国王
ll f[N][K][M];  //第一维代表长度，第二维代表用了几个国王，第三维代表二进制状态
int n, m;
int check(int num) {  //判断某状态是否有相邻的1
    for (int i = 0; i < n; i++) {
        if (((num >> i) & 1) && ((num >> (i + 1)) & 1)) return 0;
    }
    return 1;
}
int get1(int num) {  //得到某状态的1的个数
    int s = 0;
    while (num) {
        s += num % 2;
        num = num / 2;
    }
    return s;
}
signed main(int argc, char const *argv[]) {
    cin >> n >> m;
    for (int i = 0; i < 1 << n; i++) {  //判断每个状态是否可以形成，以及1的个数
        if (check(i)) vec.emplace_back(i), cnt[i] = get1(i);
    }
    int len = vec.size();
    for (int i = 0; i < len; i++) {  //枚举任何俩个状态之间是否可以转移
        for (int j = 0; j < len; j++) {
            if (((vec[i] & vec[j]) == 0) && (((vec[i] << 1) & vec[j]) == 0) &&
                (((vec[j] << 1) & vec[i]) ==
                 0))  // i状态和i<<1状态&为0，以及j<<1状态*i为0，把竖直和斜着都有1的情况卡掉
                // if ((vec[i] & vec[j]) == 0 && (check(vec[i] | vec[j])))
                // //或者让ij状态先或一下，然后再判断是否有相邻1
                h[vec[i]].emplace_back(vec[j]);
        }
    }
    f[0][0][0] = 1;
    for (int i = 1; i <= n + 1; i++) {  //多dp一行，输出答案的时候好输出
        for (int k = 0; k <= m; k++) {       //枚举国王数量
            for (int j = 0; j < len; j++) {  //枚举每个状态
                int a = vec[j];
                int lenn = h[a].size();
                for (int u = 0; u < lenn;
                     u++) {  //枚举这个状态可以从哪些状态转移过来
                    // int b = vec[h[a][u]];
                    int b = h[a][u];
                    if (k >= cnt[a]) {  //国王数量必须够我本状态转移
                        f[i][k][a] += f[i - 1][k - cnt[a]][b];
                    }
                }
            }
        }
    }
    // cout << f[n + 1][m][0] <<
    // endl;//上面dp多枚举了一行，那么就取这个一行用了0个国王的所有情况
    
    //或者把所有情况累加
    ll s = 0;
    for (int j = 0; j < len; j++) {
        s += f[n][m][vec[j]];
    }
    cout << s << endl;

    return 0;
}

View Code