B树

Posted 2023-02-23 ZDF0414

定义：一棵M（M>2）阶的平衡搜索树
性质：以下出现的 M/2 均表示向上取整
     （1）根节点至少有两个孩子
     （2）每个非根节点有[M/2,M]个孩子
     （3）每个非根节点有[M/2,M-1]个关键字，并且以升序排列
     （4）key[i]和key[i+1]之间的孩子节点的值介于key[i]、key[i+1]之间

     （5）所有的叶子节点都在同一层

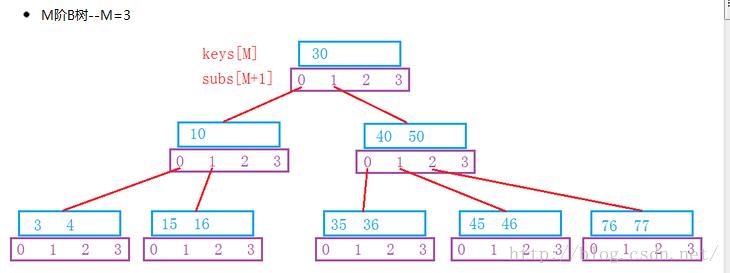
下面来实现一下B树的插入、查找、中序的操作

#pragma once
#include<iostream>
using namespace std;
template<class K, int M=3>//M：M路的B树
struct BTreeNode

	int _size;             //标识有多少key
	K _keys[M];             //一个结点最多有M-1个key值
	BTreeNode<K,M>* _parent;
	BTreeNode<K,M>* _subs[M + 1];//一个结点最多有M个子结点
	BTreeNode<K, M>()
		: _size(0)
		, _parent(0)
	
		for (int i = 0; i < M; i++)
		
			_keys[i] = 0;
			_subs[i] = NULL;
		
		_subs[M] = NULL;
	
;
template<class K,int M=3>
class BTree

	typedef BTreeNode<K, M> Node;
public:
	BTree()
		:_root(NULL)
	
	//在B树中的查找功能
	pair<Node*, int> Find(const K& key)
	
		if (_root == NULL)
			return pair<Node*, int>(NULL, -1);;
		Node*parent = NULL;
		Node*cur = _root;
		while (cur)
		
			int i = 0;
			for (; i < cur->_size; i++)//需要查询每个结点的所有key值
			
				if (cur->_keys[i] == key)
					return pair<Node*, int>(cur, i);
				else if (cur->_keys[i]>key)//确定往子树的查找方向
					break;
			
			parent = cur;
			cur = cur->_subs[i];
		
		return pair<Node*, int>(parent, -1);
	
	bool Insert(const K& key)
	
		//1、如果根结点为空
		if (_root == NULL)
		
			_root = new Node;
			_root->_keys[0] = key;
			_root->_size++;
			return true;
		
		pair<Node*, int> _pair = Find(key);
		if (_pair.second >0 )//key已存在
			return false;
		Node* cur = _pair.first;
		Node* parent = NULL;
		Node* sub = NULL;
		K NewKey = key;
		while (1)
		
			_InsertKey(cur, NewKey, sub);
			if (cur->_size < M)//key满足要求
				return true;
			
			//说明cur->_size已经超过了B-树的要求的key值个数,则就需要向上调整
			int div = (cur->_size) / 2;//往上提的key值的下标（提的是中间结点）

			Node*tmp = new Node;//把div右边的key值都拷到tmp里，作为所提结点的右孩子
			int index = 0;
			for (int i = div + 1; i < cur->_size; i++)
			
				tmp->_keys[index] = cur->_keys[i];
				cur->_keys[i] = 0;//清0操作
				tmp->_size++;
				index++;
			
			
			//再把div以右的孩子结点拷到tmp中
			index = 0;
			for (int i = div + 1; i < cur->_size+1; i++)
			
				tmp->_subs[index] = cur->_subs[i];
				cur->_subs[i] = NULL;
				index++;
			
			
			//更新cur结点，还剩下div以左的部分
			cur->_size -= (tmp->_size + 1);
			if (cur == _root)//如果cur为根节点，则div被提上去就是新的根结点
			
				_root = new Node;
				_root->_keys[0] = cur->_keys[div];
				cur->_keys[div] = 0;//清0操作
				_root->_subs[0] = cur;
				_root->_subs[1] = tmp;
				cur->_parent = _root;
				tmp->_parent = _root;
				_root->_size++;
				return true;
			
			NewKey = cur->_keys[div];
			cur->_keys[div] = 0;//清0操作
			cur = cur->_parent;
			sub = tmp;
		
	
	
	//B树的中序遍历
	void InOrder()
	
		_InOrder(_root);
		cout << endl;
	
protected:

	//把待插入的值插入到cur的_keys的适当位置，其过程就是一个插入排序的思想
	void _InsertKey(Node*cur, K& key, Node*sub)
	
		int end = cur->_size - 1;//cur->_keys的最后一个有效key的位置
		while (end >= 0)
		
			if (cur->_keys[end] > key)
			//移动keyz值的同时，也需要对比其大的孩子结点进行移动
				cur->_keys[end + 1] = cur->_keys[end];
				cur->_subs[end + 2] = cur->_subs[end + 1];
				end--;
			
			else
				break;
		
		//找准了插入位置
		cur->_keys[end + 1] = key;
		cur->_subs[end + 2] = sub;
		if (sub)
			sub->_parent = cur;
		cur->_size++;
	
	void _InOrder(Node* root)
	
		if (root == NULL)
			return;
		int i = 0;
		for (; i < root->_size; i++)
		
			_InOrder(root->_subs[i]);
			cout << root->_keys[i]<<" ";
		
		_InOrder(root->_subs[i]);
	
private:
	Node*_root;
;