并查集

Posted 2021-05-23 mrmrwjk

并查集：

1、将两个集合合并

2、询问两个元素是否在一个集合当中

基本原理：每个集合用一棵树来表示。树根的编号就是这个集合的编号。每个节点存储它的父节点，p[x]表示x的父节点

问题1：如何判断树根：if (p[x] == x)

问题2：如何求x的集合编号：while (p[x] != x) x = p[x];

问题3：如何合并两个集合：px是x的集合编号，py是y的集合编号。p[x] = y;

对并查集的优化一个方法就是压缩路径

原始的话，当两个集合合并之后长度会变长，所以路径会增加

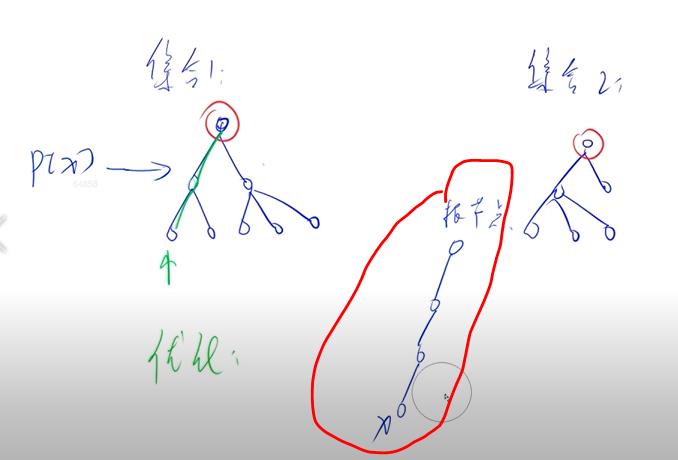
就比如图中圈起来的部分，x在找他的根节点的时候，需要向上寻找，但是每次都会花费很长的时间，我们知道这个路径上的所有节点的祖宗节点都是同一个根结点，所以我们可以将所有自己点直接连到根结点下面

优化：路径压缩

这一步的代码对应于

//返回x的祖宗节点 + 路径压缩
int find(int x) {
    if (p[x] != x) {
        p[x] = find(p[x]);   // 路径压缩
    }
    return p[x];
}

题目：合并集合

一共有 n 个数，编号是 1∼n，最开始每个数各自在一个集合中。

现在要进行 m 个操作，操作共有两种：

1. M a b，将编号为 a 和 b 的两个数所在的集合合并，如果两个数已经在同一个集合中，则忽略这个操作；
2. Q a b，询问编号为 a 和 b 的两个数是否在同一个集合中；

输入格式

第一行输入整数 n 和 m。

接下来 m 行，每行包含一个操作指令，指令为 M a b 或 Q a b 中的一种。

输出格式

对于每个询问指令 Q a b，都要输出一个结果，如果 aa 和 bb 在同一集合内，则输出 Yes，否则输出 No。

每个结果占一行。

数据范围

1≤n,m≤10⁵

输入样例：

4 5
M 1 2
M 3 4
Q 1 2
Q 1 3
Q 3 4

输出样例：

Yes
No
Yes

#include<iostream>

using namespace std;

const int N = 100010;

int n, m;
int p[N];

//返回x的祖宗节点 + 路径压缩
int find(int x) {
    if (p[x] != x) {
        p[x] = find(p[x]);
    }
    return p[x];
}



int main() {

    scanf("%d%d", &n, &m);

    for (int i = 1; i <= n; i++) {
        p[i] = i;
    }

    while (m--) {

        //小细节，这个地方之所以用字符数组去读取字符原因是因为如果直接读取字符的话，会自动读取一些空格换行
        //scanf("%c%d%d", &op, &a, &b); 这样会出现错误 所以读取字符的话，可以考虑采用读取字符串的形式
        char op[2];
        int a, b;
        scanf("%s%d%d", op, &a, &b);

        if (op[0] == \'M\') {
            p[find(a)] = find(b);
        }



    }






    return 0;
}

题型二：连通块中点的数量

注意这个时候需要维护一些变量

给定一个包含 n 个点（编号为 1∼n）的无向图，初始时图中没有边。

现在要进行 m 个操作，操作共有三种：

1. C a b，在点 a 和点 b 之间连一条边，a 和 b 可能相等；
2. Q1 a b，询问点 a 和点 b 是否在同一个连通块中，a 和 b 可能相等；
3. Q2 a，询问点 a 所在连通块中点的数量；

输入格式

第一行输入整数 n 和 m。

接下来 m 行，每行包含一个操作指令，指令为 C a b，Q1 a b 或 Q2 a 中的一种。

输出格式

对于每个询问指令 Q1 a b，如果 a 和 b 在同一个连通块中，则输出 Yes，否则输出 No。

对于每个询问指令 Q2 a，输出一个整数表示点 a 所在连通块中点的数量

每个结果占一行。

数据范围

1≤n,m≤10⁵

输入样例：

5 5
C 1 2
Q1 1 2
Q2 1
C 2 5
Q2 5

输出样例：

Yes
2
3

#include<iostream>

using namespace std;

const int N = 100010;

int n, m;
int p[N], size1[N];


//返回x的祖宗节点 + 路径压缩
int find(int x) {
    if (p[x] != x) {
        //递归进行路径压缩
        p[x] = find(p[x]);
    }
    return p[x];
}



int main() {

    scanf("%d%d", &n, &m);

    for (int i = 1; i <= n; i++) {
        p[i] = i;
        size1[i] = 1;
    }

    while (m--) {

        //小细节，这个地方之所以用字符数组去读取字符原因是因为如果直接读取字符的话，会自动读取一些空格换行
        //scanf("%c%d%d", &op, &a, &b); 这样会出现错误 所以读取字符的话，可以考虑采用读取字符串的形式
        char op[5];
        int a, b;
        scanf("%s", op);

        if (op[0] == \'C\') {
            scanf("%d%d", &a, &b);
            //判断两个点是否有同一个祖宗节点，如果是的话，那么size不用相加
            if (find(a) == find(b)) {
                continue;
            }
            size1[find(b)] += size1[find(a)];
            p[find(a)] = find(b);
        } else if (op[1] == \'1\'){
            scanf("%d%d", &a, &b);
            if (find(a) == find(b)) {
                puts("Yes");
            } else {
                puts("No");
            }
        } else {
            scanf("%d", &a);
            printf("%d\\n", size1[find(a)]);
        }

    }



//    for (int i = 1; i <= n; i++) {
//        cout << p[i];
//    }



    return 0;
}