普里姆(Prim)算法
Posted kokiafan
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了普里姆(Prim)算法相关的知识,希望对你有一定的参考价值。
概览
普里姆算法(Prim算法),图论中的一种算法,可在加权连通图(即“带权图”)里搜索最小生成树。即此算法搜索到的边(Edge)子集所构成的树中,不但包括了连通图里的所有顶点(Vertex)且其所有边的权值之和最小。
(注:N个顶点的图中,其最小生成树的边为N-1条,且各边之和最小。树的每一个节点(除根节点)有且只有一个前驱,所以,只有N-1条边。)
该算法于1930年由捷克数学家沃伊捷赫·亚尔尼克(Vojtěch Jarník)发现;并在1957年由美国计算机科学家罗伯特·普里姆(Robert C. Prim)独立发现;1959年,艾兹格·迪科斯彻再次发现了该算法。因此,在某些场合,普里姆算法又被称为DJP算法、亚尔尼克算法或普里姆-亚尔尼克算法。
定义
假设G=(V, {E})是连通网,TE是N上最小生成树中边(Edge)的集合。V是图G的顶点的集合,E是图G的边的集合。算法从U={u0} (u0∈V),TE={}开始。重复执行下述操作:
- 在所有u∈U,v∈V-U的边(u, v)∈E中找一条代价(权值)最小的边(u0, v0)并入集合TE。
- 同时v0并入U
- 直至U=V为止。此时TE中必有n-1条边,则T=(V, {TE})为N的最小生成树。
由算法代码中的循环嵌套可得知此算法的时间复杂度为O(n2)。
过程简述
输入:带权连通图(即“网”)G,其顶点的集合为V,边的集合为E。
初始:U={u},u为从V中任意选取顶点,作为起始点;TE={}。
操作:重复以下操作,直到U=V,即两个集合相等。
- 在集合E中选取权值最小的边(u, v),u∈U,v∈V且v∉U。(如果存在多条满足前述条件,即权值相同的边,则可任意选取其中之一。)
- 将v并入U,将(u, v)边加入TE。
输出:用集合U和TE来描述所得到的最小生成树。
如何实现
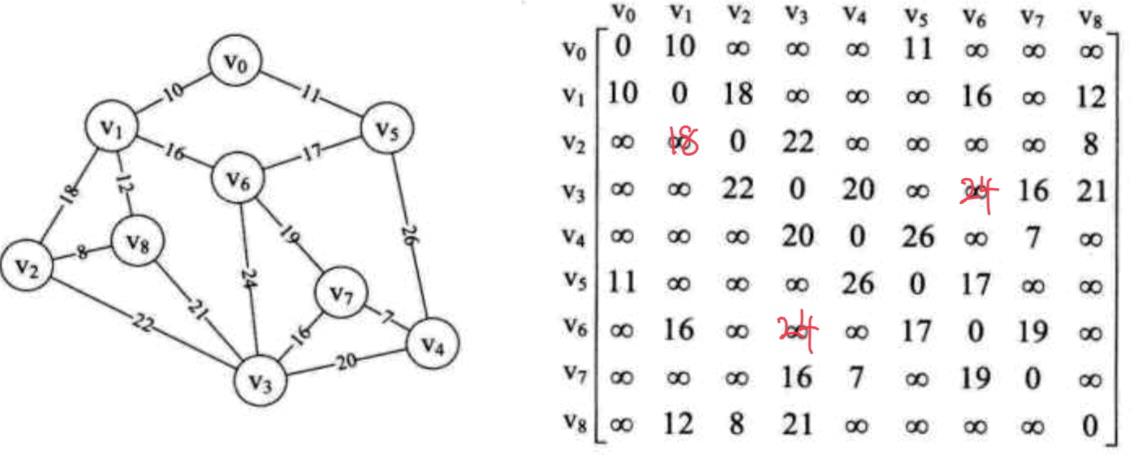
如上面的这个图G=(V, {E}),其中:
V={v0, v1, v2, v3, v4, v5, v6, v7, v8},
E= {(v0, v1), (v0, v5), (v1, v6), (v5, v6), (v1, v8), (v1, v2), (v2, v8), (v6, v7), (v3, v6), (v4, v5), (v4, v7), (v3, v7), (v3, v4), (v3,v8), (v2, v3)}
用邻接矩阵表示该图G,得上图右边的邻接矩阵。
此图G有n = 9个顶点,其最小生成树则必有n-1 = 8条边。
(注意:图G的最小生成树是一棵树,且图G中的每个顶点都在这棵树里,故必含有n个顶点;而除树根节点,每个节点有且只有一个前驱,所以图G的最小生成树有且只有n-1条边。若边数大于n-1,则必有树中某个顶点与另一个顶点存在第二条边,从而不能构成树。树中节点是一对多关系而不是多对多关系。)
①输入:带权连通图G=(V, {E}),求图G的最小生成树。
②初始:U={u},取图G中的v0作为u,用数组adjVex=int[9]来表示U(最终U要等于V),adjVex数组记录的是U中顶点的下标。U是最小生成树T的各边的起始顶点的集合。
adjVex初始值为[0, 0, 0, 0, 0, 0, 0, 0, 0],表示从顶点v0开始去寻找权值最小的边。
用数组lowCost = int[9] 表示adjVex中各点到集合V中顶点构成的边的权值。lowCost数组中元素的索引即是顶点V的下标。解释:adjVex[3] == 0,表示v0,adjVex[5] == 0,表示v0。lowCost[3] == ∞且adjVex[3] == 0,表示(v0, v3)边不存在;lowCost[5] == 11且adjVex[5] == 0,表示(v0, v5)边的权值为11。
如:邻接矩阵中的v0行,v0顶点与各顶点构成的边及其权值用下面这的方式表示:
示例一
索引:index [0, 1, 2, 3, 4, 5, 6, 7, 8]
权值:lowCost[0, 10, ∞, ∞, ∞, 11, ∞, ∞, ∞]
下标:adjVex [0, 0, 0, 0, 0, 0, 0, 0, 0](v0, v0, 0), (v0, v3, ∞), (v0, v5, 11)
0表示以该顶点为终点的边已经并入图G的最小生成树的边集合——TE集合,不需要再比较(搜索)。
∞表示以该顶点为终点的边不存在。
③操作:
- 上面示例一中,最小的权值为10,此时lowCost中下标k = 1,相应地adjVex[k]即adjVex[1] == 0,记录下此时的边为(v0, v1)。
- 将adjVex[k]即adjVex[1]设为1,表示将顶点v1放入图G的最小生成树的顶点集合U中。
- 将lowCost[k]即lowCost[1]设为0,表示以v1为终止点的边已搜索。
- 然后,将焦点转向顶点v1,看看从v1开始的边有哪些是权值小于从之前的顶点v0开始的边的。此时k == 1。则有以下过程:
索引:index [ 0, 1, 2, 3, 4, 5, 6, 7, 8]
权值:lowCost[ 0, 0, ∞, ∞, ∞, 11, ∞, ∞, ∞]
下标:adjVex [ 0, 1, 0, 0, 0, 0, 0, 0, 0]
顶点:vex[1] [10, 0,18, ∞, ∞, ∞,16, ∞,12]
由于lowCost[0]和lowCost[1]为0,所以从lowCost[2]开始比较权值。vex[1][2] == 18 < lowCost[2],意思是(v0, v2)==∞不存在这条边,(v1, v2) == 18,存在权为18的边(v1, v2),类似的还有vex[1][6] == 16 < lowCost[6]和vex[1][8] == 12 < lowCost[8]。
把k == 1赋值给
adjVex[2]、adjVex[6]和adjVex[8]。
把权值18、16和12赋值给
lowCost[2]、lowCost[6]和lowCost[8]。
更新后的权值数组和邻接顶点数组如下:
索引:index [ 0, 1, 2, 3, 4, 5, 6, 7, 8]
权值:lowCost[ 0, 0, 18, ∞, ∞, 11, 16, ∞, 12]
下标:adjVex [ 0, 1, 1, 0, 0, 0, 1, 0, 1]
故下次循环从顶点v1为起点去搜索lowCost中权值最小的边。如此往复循环,直到图G中的每一个顶点都被遍历到。(邻接矩阵的每一行都被遍历到)
④输出:
演示过程
Loop 1
lowCost: [ 0, 10, ∞, ∞, ∞, 11, ∞, ∞, ∞ ]
adjVex: [ 0, 0, 0, 0, 0, 0, 0, 0, 0 ]
lowCost: [ 0, 0, 18, ∞, ∞, 11, 16, ∞, 12 ]
adjVex: [ 0, 1, 1, 0, 0, 0, 1, 0, 1 ]
Loop 2
lowCost: [ 0, 0, 18, ∞, ∞, 11, 16, ∞, 12 ]
adjVex: [ 0, 1, 1, 0, 0, 0, 1, 0, 1 ]
lowCost: [ 0, 0, 18, ∞, 26, 0, 16, ∞, 12 ]
adjVex: [ 0, 1, 5, 0, 5, 0, 1, 0, 1 ]
Loop 3
lowCost: [ 0, 0, 18, ∞, 26, 0, 16, ∞, 12 ]
adjVex: [ 0, 1, 5, 0, 5, 0, 1, 0, 1 ]
lowCost: [ 0, 0, 8, 21, 26, 0, 16, ∞, 0 ]
adjVex: [ 0, 1, 8, 8, 5, 0, 1, 0, 1 ]
Loop 4
lowCost: [ 0, 0, 8, 21, 26, 0, 16, ∞, 0 ]
adjVex: [ 0, 1, 8, 8, 5, 0, 1, 0, 1 ]
lowCost: [ 0, 0, 0, 21, 26, 0, 16, ∞, 0 ]
adjVex: [ 0, 1, 8, 8, 2, 0, 1, 0, 1 ]
Loop 5
lowCost: [ 0, 0, 0, 21, 26, 0, 16, ∞, 0 ]
adjVex: [ 0, 1, 8, 8, 2, 0, 1, 0, 1 ]
lowCost: [ 0, 0, 0, 21, 26, 0, 0, 19, 0 ]
adjVex: [ 0, 1, 8, 8, 2, 6, 1, 6, 1 ]
Loop 6
lowCost: [ 0, 0, 0, 21, 26, 0, 0, 19, 0 ]
adjVex: [ 0, 1, 8, 8, 2, 6, 1, 6, 1 ]
lowCost: [ 0, 0, 0, 16, 7, 0, 0, 0, 0 ]
adjVex: [ 0, 1, 8, 7, 7, 6, 7, 6, 1 ]
Loop 7
lowCost: [ 0, 0, 0, 16, 7, 0, 0, 0, 0 ]
adjVex: [ 0, 1, 8, 7, 7, 6, 7, 6, 1 ]
lowCost: [ 0, 0, 0, 16, 0, 0, 0, 0, 0 ]
adjVex: [ 0, 1, 8, 7, 7, 6, 7, 4, 1 ]
Loop 8
lowCost: [ 0, 0, 0, 16, 0, 0, 0, 0, 0 ]
adjVex: [ 0, 1, 8, 7, 7, 6, 7, 4, 1 ]
lowCost: [ 0, 0, 0, 0, 0, 0, 0, 0, 0 ]
adjVex: [ 0, 1, 8, 7, 7, 6, 7, 4, 3 ]
运行结果
(0, 1)
(0, 5)
(1, 8)
(8, 2)
(1, 6)
(6, 7)
(7, 4)
(7, 3)
算法代码
C#代码
using System;
namespace Prim
{
class Program
{
static void Main(string[] args)
{
int numberOfVertexes = 9,
infinity = int.MaxValue;
int[][] graph = new int[][] {
new int[]{0, 10, infinity, infinity, infinity, 11, infinity, infinity, infinity },
new int[]{ 10, 0, 18, infinity, infinity, infinity, 16, infinity, 12 },
new int[]{ infinity, 18, 0, 22, infinity, infinity, infinity, infinity, 8 },
new int[]{ infinity, infinity, 22, 0, 20, infinity, 24, 16, 21 },
new int[]{ infinity, infinity, infinity, 20, 0, 26, infinity, 7, infinity },
new int[]{ 11, infinity, infinity, infinity, 26, 0, 17, infinity, infinity },
new int[]{ infinity, 16, infinity, 24, infinity, 17, 0, 19, infinity },
new int[]{ infinity, infinity, infinity, 16, 7, infinity, 19, 0, infinity },
new int[]{ infinity, 12, 8, 21, infinity, infinity, infinity, infinity, 0 },
};
//Prim(graph, numberOfVertexes);
PrimSimplified(graph, numberOfVertexes);
}
static void Prim(int[][] graph, int numberOfVertexes)
{
bool debug = true;
int[] adjVex = new int[numberOfVertexes], // 邻接顶点数组:搜索边的最小权值过程中各边的起点坐标
lowCost = new int[numberOfVertexes]; // 各边权值数组:搜索边的最小权值过程中各边的权值,数组下标为边的终点。
for (int i = 0; i < numberOfVertexes; i++) // 从图G的下标为0的顶点开始搜索。(也是图G的最小生成树的顶点集合)。
{
adjVex[i] = 0;
}
for (int i = 0; i < numberOfVertexes; i++) // 初始从下标为0的顶点开始到下标为i的顶点的边的权值去搜索。找lowCost中权值最小的下标i。
{
lowCost[i] = graph[0][i];
}
int k = 0; // 初始假定权值最小的边的终点的下标为k。
for (int i = 1; i < numberOfVertexes; i++)
{
if (debug)
{
Console.WriteLine($"Loop {i}");
Console.Write("lowCost: ");
PrintArray(lowCost);
Console.Write(" adjVex: ");
PrintArray(adjVex);
Console.WriteLine();
}
int minimumWeight = int.MaxValue; // 搜索过程中发现到的最小的权值。初始设置为最大的整数值以示两点间无边。
for (int j = 1; j < numberOfVertexes; j++)
{
if (lowCost[j] != 0 && lowCost[j] < minimumWeight) // lowCost中0表示该点已经搜索过了。lowCost[j] < minimumWeight即发现目前最小权值。
{
minimumWeight = lowCost[j]; // 发现目前最小权值。
k = j; // 目前最小权值的边的终点下标。
}
}
if (!debug)
{
Console.WriteLine($"({adjVex[k]}, {k})"); // 输出边
}
adjVex[i] = k; // 此时找到的k值即是权值最小的边的终点。将V[k]放入集合U。(这步可省略,因lowCost[j]已被标为“无需搜索”了)。
lowCost[k] = 0; // 0表示该点已经搜索过了,已不需要再被搜索了。
for (int j = 1; j < numberOfVertexes; j++) // 转到以V[k]为开始顶点的边,去与前面u为起始顶点到V[i]为终止顶点的边的权值去比较。
{
if (lowCost[j] != 0 && graph[k][j] < lowCost[j]) // lowCost中0表示该点已经搜索过了。graph[k][j] < lowCost[j]即发现更小权值。
{
lowCost[j] = graph[k][j]; // 更新权值;索引j即终点下标。
adjVex[j] = k; // 下次寻找权值小的边时,从k为下标的顶点为起点。
}
}
if (debug)
{
Console.Write("lowCost: ");
PrintArray(lowCost);
Console.Write(" adjVex: ");
PrintArray(adjVex);
Console.WriteLine();
}
}
}
static void PrimSimplified(int[][] graph, int numberOfVertexes)
{
int[] adjVex = new int[numberOfVertexes], // 邻接顶点数组:搜索边的最小权值过程中各边的起点坐标
lowCost = new int[numberOfVertexes]; // 各边权值数组:搜索边的最小权值过程中各边的权值,数组下标为边的终点。
for (int i = 0; i < numberOfVertexes; i++)
{
adjVex[i] = 0; // 从图G的下标为0的顶点开始搜索。(也是图G的最小生成树的顶点集合)。
lowCost[i] = graph[0][i]; // 初始从下标为0的顶点开始到下标为i的顶点的边的权值去搜索。找lowCost中权值最小的下标i。
}
int k = 0; // 初始假定权值最小的边的终点的下标为k。
for (int i = 1; i < numberOfVertexes; i++)
{
int minimumWeight = int.MaxValue; // 搜索过程中发现到的最小的权值。初始设置为最大的整数值以示两点间无边。
for (int j = 1; j < numberOfVertexes; j++)
{
if (lowCost[j] != 0 && lowCost[j] < minimumWeight) // lowCost中0表示该点已经搜索过了。lowCost[j] < minimumWeight即发现目前最小权值。
{
minimumWeight = lowCost[j]; // 发现目前最小权值。
k = j; // 目前最小权值的边的终点下标。
}
}
Console.WriteLine($"({adjVex[k]}, {k})"); // 输出边
lowCost[k] = 0; // 0表示该点已经搜索过了,已不需要再被搜索了。
for (int j = 1; j < numberOfVertexes; j++) // 转到以V[k]为开始顶点的边,去与前面u为起始顶点到V[i]为终止顶点的边的权值去比较。
{
if (lowCost[j] != 0 && graph[k][j] < lowCost[j]) // lowCost中0表示该点已经搜索过了。graph[k][j] < lowCost[j]即发现更小权值。
{
lowCost[j] = graph[k][j]; // 更新权值;索引j即终点下标。
adjVex[j] = k; // 下次寻找权值小的边时,从k为下标的顶点为起点。
}
}
}
}
static void PrintArray(int[] array)
{
Console.Write("[ ");
for (int i = 0; i < array.Length - 1; i++) // 输出数组的前面n-1个
{
Console.Write($"{ToInfinity(array[i])}, ");
}
if (array.Length > 0) // 输出数组的最后1个
{
int n = array.Length - 1;
Console.Write($"{ToInfinity(array[n])}");
}
Console.WriteLine(" ]");
}
static string ToInfinity(int i) => i == int.MaxValue ? "∞" : i.ToString();
}
}
TypeScript代码
function prim(graph: number[][], numberOfVertexes: number) {
let debug: boolean = true;
let adjVex: number[] = [], // 邻接顶点数组:搜索边的最小权值过程中各边的起点坐标
lowCost = []; // 各边权值数组:搜索边的最小权值过程中各边的权值,数组下标为边的终点。
for (let i = 0; i < numberOfVertexes; i++) // 从图G的下标为0的顶点开始搜索。(也是图G的最小生成树的顶点集合)。
{
adjVex[i] = 0;
}
for (let i = 0; i < numberOfVertexes; i++) // 初始从下标为0的顶点开始到下标为i的顶点的边的权值去搜索。找lowCost中权值最小的下标i。
{
lowCost[i] = graph[0][i];
}
let k: number = 0; // 初始假定权值最小的边的终点的下标为k。
for (let i = 1; i < numberOfVertexes; i++) {
if (debug) {
console.log(`Loop ${i}`);
console.log(`lowCost: ${printArray(lowCost)}`);
console.log(` adjVex: ${printArray(adjVex)}`);
}
let minimumWeight: number = Number.MAX_VALUE; // 搜索过程中发现到的最小的权值。初始设置为最大的整数值以示两点间无边。
for (let j = 1; j < numberOfVertexes; j++) {
if (lowCost[j] != 0 && lowCost[j] < minimumWeight) // lowCost中0表示该点已经搜索过了。lowCost[j] < minimumWeight即发现目前最小权值。
{
minimumWeight = lowCost[j]; // 发现目前最小权值。
k = j; // 目前最小权值的边的终点下标。
}
}
if (!debug) {
console.log(`(${adjVex[k]}, ${k})`);// 输出边
}
adjVex[i] = k; // 此时找到的k值即是权值最小的边的终点。将V[k]放入集合U。(这步可省略,因lowCost[j]已被标为“无需搜索”了)。
lowCost[k] = 0; // 0表示该点已经搜索过了,已不需要再被搜索了。
for (let j = 1; j < numberOfVertexes; j++) // 转到以V[k]为开始顶点的边,去与前面u为起始顶点到V[i]为终止顶点的边的权值去比较。
{
if (lowCost[j] != 0 && graph[k][j] < lowCost[j]) // lowCost中0表示该点已经搜索过了。graph[k][j] < lowCost[j]即发现更小权值。
{
lowCost[j] = graph[k][j]; // 更新权值;索引j即终点下标。
adjVex[j] = k; // 下次寻找权值小的边时,从k为下标的顶点为起点。
}
}
if (debug) {
console.log(`lowCost: ${printArray(lowCost)}`);
console.log(` adjVex: ${printArray(adjVex)}`);
console.log(\'\');
}
}
}
function primSimplified(graph: number[][], numberOfVertexes: number) {
let adjVex: number[] = [], // 邻接顶点数组:搜索边的最小权值过程中各边的起点坐标
lowCost = []; // 各边权值数组:搜索边的最小权值过程中各边的权值,数组下标为边的终点。
for (let i = 0; i < numberOfVertexes; i++) {
adjVex[i] = 0; // 从图G的下标为0的顶点开始搜索。(也是图G的最小生成树的顶点集合)。
lowCost[i] = graph[0][i]; // 初始从下标为0的顶点开始到下标为i的顶点的边的权值去搜索。找lowCost中权值最小的下标i。
}
let k: number = 0; // 初始假定权值最小的边的终点的下标为k。
for (let i = 1; i < numberOfVertexes; i++) {
let minimumWeight: number = Number.MAX_VALUE; // 搜索过程中发现到的最小的权值。初始设置为最大的整数值以示两点间无边。
for (let j = 1; j < numberOfVertexes; j++) {
if (lowCost[j] != 0 && lowCost[j] < minimumWeight) // lowCost中0表示该点已经搜索过了。lowCost[j] < minimumWeight即发现目前最小权值。
{
minimumWeight = lowCost[j]; // 发现目前最小权值。
k = j; // 目前最小权值的边的终点下标。
}
}
console.log(`(${adjVex[k]}, ${k})`); // 输出边
lowCost[k] = 0; // 0表示该点已经搜索过了,已不需要再被搜索了。
for (let j = 1; j < numberOfVertexes; j++) // 转到以V[k]为开始顶点的边,去与前面u为起始顶点到V[i]为终止顶点的边的权值去比较。
{
if (lowCost[j] != 0 && graph[k][j] < lowCost[j]) // lowCost中0表示该点已经搜索过了。graph[k][j] < lowCost[j]即发现更小权值。
{
lowCost[j] = graph[k][j]; // 更新权值;索引j即终点下标。
adjVex[j] = k; // 下次寻找权值小的边时,从k为下标的顶点为起点。
}
}
}
}
function printArray(array: number[]): string {
let str: string[] = [];
str.push("[ ");
for (let i = 0; i < array.length - 1; i++) // 输出数组的前面n-1个
{
str.push(`${toInfinity(array[i])}, `)
}
if (array.length > 0) // 输出数组的最后1个
{
let n: number = array.length - 1;
str.push(`${toInfinity(array[n])}`);
}
str.push(" ]");
return str.join("");
}
function toInfinity(i: number) {
return i == Number.MAX_VALUE ? "∞" : i.toString();
}
function Main() {
let numberOfVertexes: number = 9,
infinity = Number.MAX_VALUE;
let graph: number[][] = [
[0, 10, infinity, infinity, infinity, 11, infinity, infinity, infinity],
[10, 0, 18, infinity, infinity, infinity, 16, infinity, 12],
[infinity, 18, 0, 22, infinity, infinity, infinity, infinity, 8],
[infinity, infinity, 22, 0, 20, infinity, 24, 16, 21],
[infinity, infinity, infinity, 20, 0, 26, infinity, 7, infinity],
[11, infinity, infinity, infinity, 26, 0, 17, infinity, infinity],
[infinity, 16, infinity, 24, infinity, 17, 0, 19, infinity],
[infinity, infinity, infinity, 16, 7, infinity, 19, 0, infinity],
[infinity, 12, 8, 21, infinity, infinity, infinity, infinity, 0],
];
// let graph: number[][] = [
// [0, 1, 5, infinity, infinity, infinity, infinity, infinity, infinity],
// [1, 0, 3, 7, 5, infinity, infinity, infinity, infinity],
// [5, 3, 0, infinity, 1, 7, infinity, infinity, infinity],
// [infinity, 7, infinity, 0, 2, infinity, 3, infinity, infinity],
// [infinity, 5, 1, 2, 0, 3, 6, 9, infinity],
// [infinity, infinity, 7, infinity, 3, 0, infinity, 5, infinity],
// [infinity, infinity, infinity, 3, 6, infinity, 0, 2, 7],
// [infinity, infinity, infinity, infinity, 9, 5, 2, 0, 4],
// [infinity, infinity, infinity, infinity, infinity, infinity, 7, 4, 0],
// ];
//prim(graph, numberOfVertexes);
primSimplified(graph, numberOfVertexes);
}
Main();
/**
运行结果:
(0, 1)
(1, 2)
(2, 4)
(4, 3)
(4, 5)
(3, 6)
(6, 7)
(7, 8)
*/
参考资料:
《大话数据结构》 - 程杰 著 - 清华大学出版社 第247页
之前不会Markdown语法的角标(Subscript),所以分成了两篇文章。这里将之前的合成整理为一篇。
以上是关于普里姆(Prim)算法的主要内容,如果未能解决你的问题,请参考以下文章