[AGC022E] Median Replace 题解

Posted 2021-05-22 Robert_JYH

题意

对于一个\\(\\mathtt{01}\\)串我们每次可将\\(3\\)个连续的字符替换成这三个数的中位数，如果最后可以得到长度为\\(1\\)的字符串\\(\\mathtt{1}\\),我们称这个字符串是漂亮的。

现有\\(1\\)个长度为奇数的\\(\\mathtt{01}\\)串\\(s\\) 其中有若干位置是\\(？\\),表示该字符可以被替换为\\(\\mathtt{0,1}\\)中的任意一个字符，求这个字符串可以表示多少个不同的漂亮的字符串，答案对 $ 10^{9}\\ +\\ 7 $ 取模。

\\(|S|\\le 300000\\)

题解

本篇题解基本上为yhx大佬的题解的总结，更详细的题解请参见大佬的博客。

这类字符串问题常常需要我们写出状态的转移数组再进行DP。

1.操作分类

我们首先考虑如何判断一个串是否是漂亮的。

我们发现操作可以分为三种：

1.\\(\\texttt{000} \\to \\texttt{0}\\)

2.去掉相邻的一对 \\(\\texttt 0, \\texttt 1\\)

3.\\(\\texttt{111} \\to \\texttt{1}\\)

2.操作优先级

可以发现这三类操作有优先级，优先级为\\(1>2>3\\)

我们考虑如何证明这个优先级。

首先，容易发现，如何一个串\\(S\\)是漂亮的，那么将\\(S\\)中的一些\\(\\mathtt{0}\\)替换为\\(\\mathtt{1}\\)后其仍是漂亮的，因为我们仍然可以按照原先的操作序列进行操作。

如果当前字符串为\\(S = a \\cdot \\texttt{0001} \\cdot b\\) ,假设我们通过操作2得到的\\(S\' = a \\cdot \\texttt{00} \\cdot b\\)是漂亮的，那么我们通过操作1得到的\\(S\'\' = a \\cdot \\texttt{01} \\cdot b\\)也是漂亮的，即通过操作2可以得到的合法操作序列通过操作1也一定能得到，操作1优先于操作2，运用类似的方法可以证明操作2优先于操作3。

3.贪心判断算法

我们现在得到了一个贪心的判断算法：

1.维护一个栈，如果栈顶三个字符为\\(\\mathtt{000}\\)，则弹出其中两个\\(\\mathtt{0}\\)

2.如果栈顶为\\(\\mathbb{1}\\)，次栈顶为\\(\\mathtt{0}\\)，也立即弹出两个字符；如果栈顶为\\(\\mathbb{0}\\)，次栈顶为\\(\\mathtt{1}\\)，就先留着，因为可能会遇到连续三个\\(\\mathtt{0}\\)的更优情况

3.在这种贪心的过程中，一旦栈内出现了连续两个\\(\\mathtt{1}\\)，就可以说明该字符串一定是漂亮的，因为我们可以先把后面的合并了再合并这两个\\(1\\)，从而得到\\(1\\)

自此我们得到了\\(O(n)\\)的判断算法。

4.自动机跑匹配

我们发现栈内状态及弹出的过程很像自动机的状态及转移，于是我们可以写出状态的转移数组再进行自动机上的DP。

自动机如下(S表示空节点)：

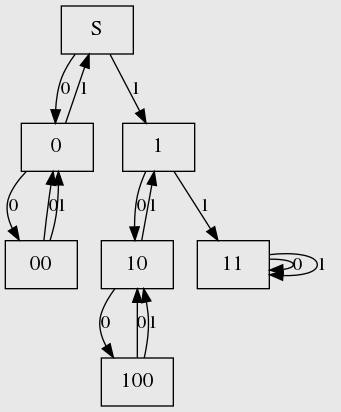
我们在自动机上跑匹配即可。

#include<bits/stdc++.h>
using namespace std;
const int N=3e5+5;
const int mod=1e9+7;
#define add(a,b) a=(a+b)%mod
char s[N];
int f[N][7],g[2][7]={{1,3,4,1,6,5,4},{2,0,5,1,2,5,4}};
int main(){
	scanf("%s",s+1);
	int n=strlen(s+1);
	f[0][0]=1;
	for(int i=0;i<n;i++)
		for(int j=0;j<7;j++){
			if(s[i+1]!=\'1\')add(f[i+1][g[0][j]],f[i][j]);
			if(s[i+1]!=\'0\')add(f[i+1][g[1][j]],f[i][j]);
		}
	printf("%d\\n",(f[n][2]+f[n][5])%mod);
	return 0;
}