《Ray Tracing in One Weekend》阅读笔记

Posted 2021-05-20 shadow_lr

不发光的漫射对象仅具有周围环境的颜色，但是会使用其自身的固有颜色对其进行调制。从散射表面反射的光的方向随机化。因此，如果我们将三束光线发送到两个扩散表面之间的裂缝中，它们将具有不同的随机行为：

8.1.A Simple Diffuse Material（ 一种简单的扩散材料）

不发光的漫射对象仅具有周围环境的颜色，但是会使用其自身的固有颜色对其进行调制。从散射表面反射的光的方向随机化。因此，如果我们将三束光线发送到两个扩散表面之间的裂缝中，它们将具有不同的随机行为：

Figure 8: Light ray bounces

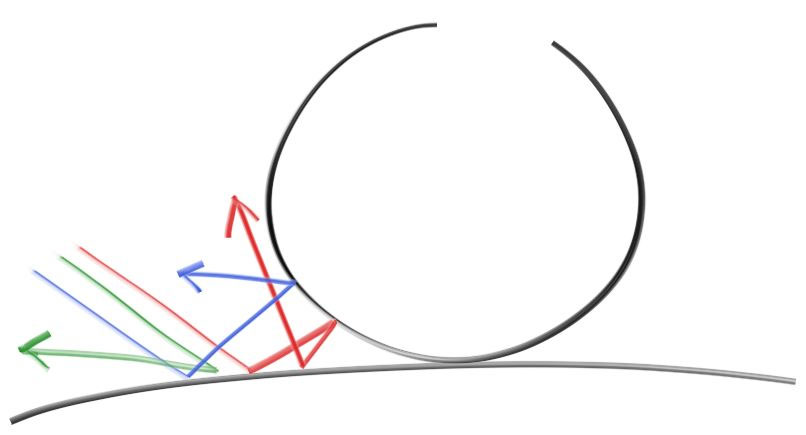
它们也可能被吸收而不是被反映出来。 表面越黑，吸收的可能性就越大。（这就是为什么它很暗的原因！）实际上，任何将方向随机化的算法都会产生看起来粗糙的表面。 事实证明，最简单的方法之一是对理想的扩散表面完全正确。 （我以前把它作为一个懒惰的黑客，在数学上接近理想的Lambertian。）

可以理解为当光线射向几何体上某点时，如果此点反弹后会接着与其他几何体有交点，那么光的能量会在陆续在反射中损失一定的能量，如果光线射向几何体后，不会弹射到其他几何体，那么可视为该点所获得的光的能量是最大的，也就呈现明亮的样子，如果射向几何体后，再弹回其他几何体，那么可视为最初光线（射线）与几何体的交点吸收了大部分能量，所以呈现为黑色（暗色）

（读者Vassillen Chizhov证明了懒惰黑客确实只是一个懒惰黑客，而且是不准确的。理想的Lambertian的正确表示并不需要太多工作，并且在本章的结尾处进行了介绍。）

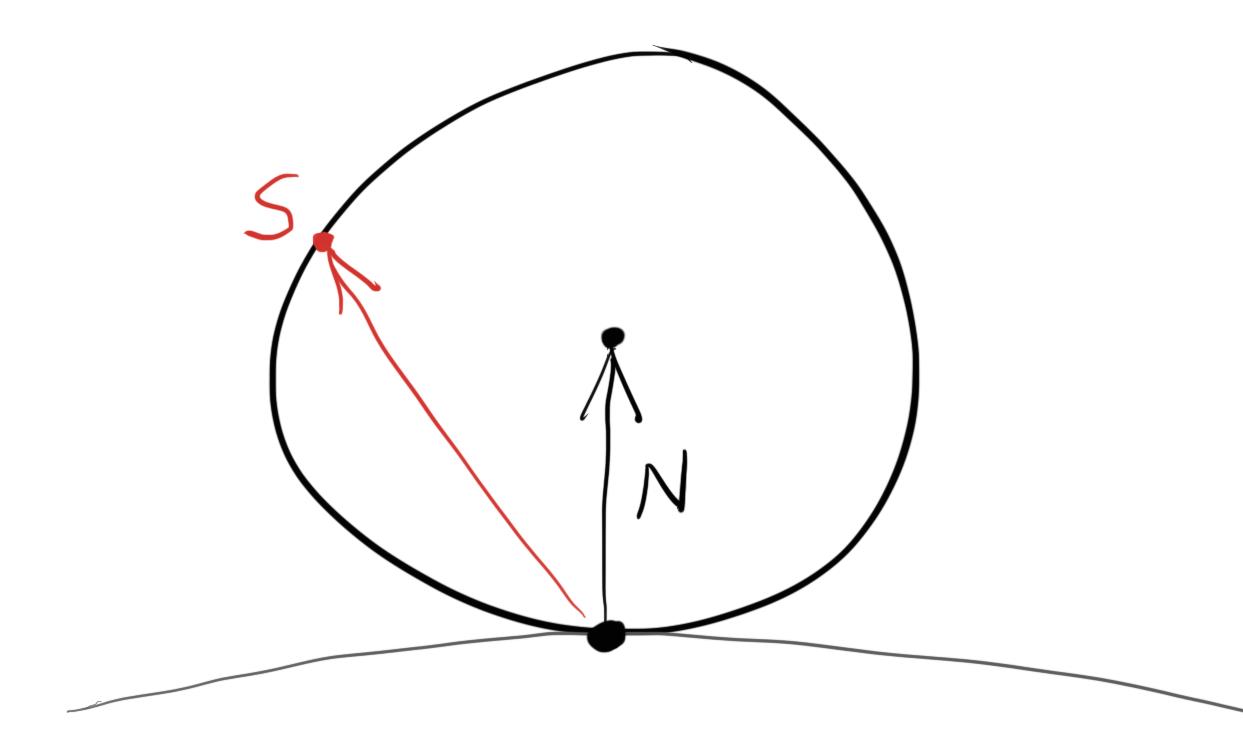
有两个单位半径球体与曲面的切点p相切。 这两个球的中心为（P + n）和（PN），其中n为曲面的法线。 以（P-n）为中心的球体被视为曲面的内部，而以（P + n）为中心的球体被视为曲面的外部。 选择与射线原点在曲面同一侧的切线单位半径球体。 在此单位半径球体内选取一个随机点S，然后将一条光线从命中点P发送到随机点S（这是矢量（S-P））：

Figure 9: Generating a random diffuse bounce ray

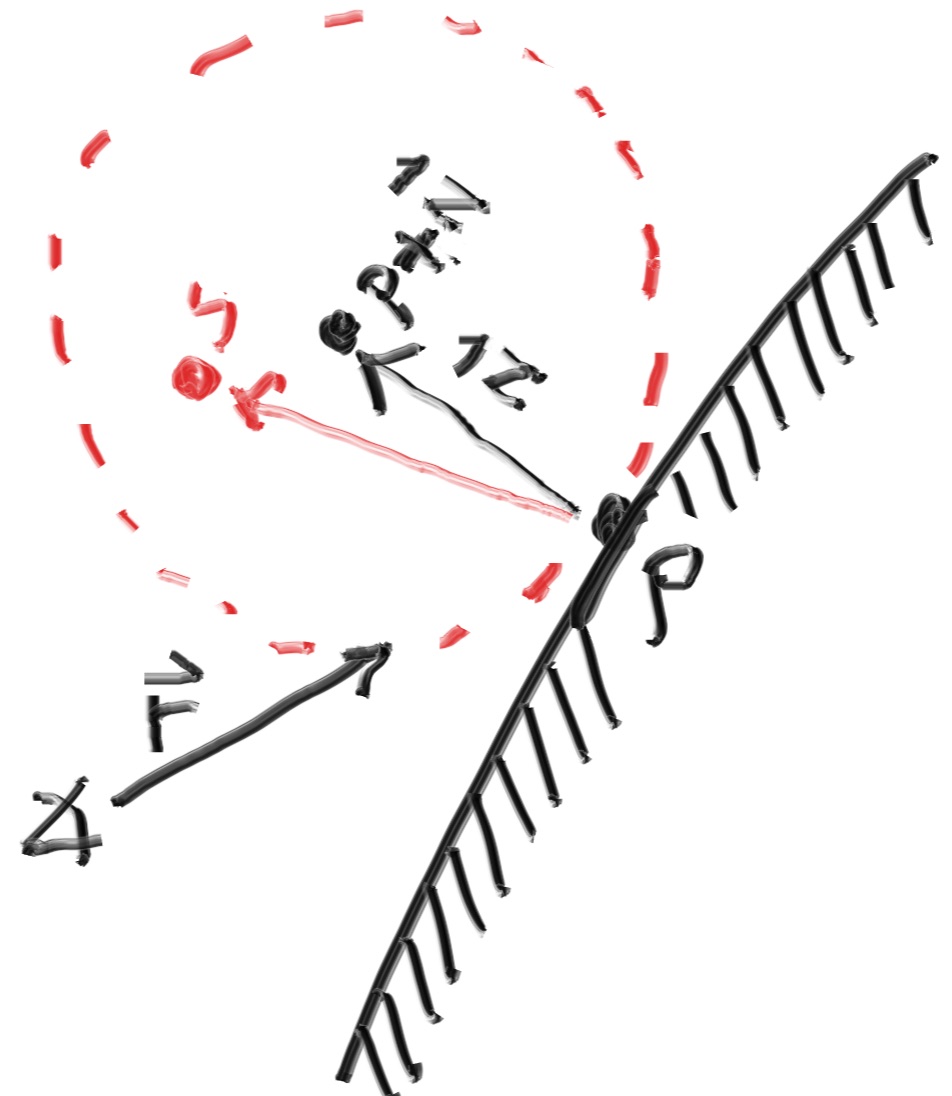
我们需要一种在单位半径球体内选择随机点的方法。 我们将使用通常最简单的算法：拒绝法。

首先，在单位立方体中选择一个随机点，其中x，y和z的范围都在-1到+1之间。 如果该随机点的x，y，z不满足在圆内条件则拒绝该点，该点在球体之外然后重复操作。

有两个单位半径球体与曲面的切点pp相切。 这两个球的中心为（P + n）（P + n）和（P-n）（P-n），其中nn是曲面的法线。 以（P-n）（P-n）为中心的球体被认为是表面的内部，而以（P + n）（P + n）的中心为球体的外部是表面。 选择与射线原点在曲面同一侧的切线单位半径球体。 在此单位半径球体内选取一个随机点SS，然后将一条射线从撞击点PP发送到随机点SS（这是向量（S-P）（S-P））：

效果

这是没有加上反走样的情况下生成的图，反走样会加大图像生成时间，所以暂时先去掉，效果如下，表面出现了很多的黑色噪点，其实是各个颜色的rgb组在一起不统一，视觉上有多余的颜色（杂）

当加大采样点并且计算周围点的rgb平均到像素中心点的rgb后效果如下（可以看到不像上图那样有颗粒状），颜色比较平均，仔细观察球的周围有抗锯齿效果，但这样会加大计算时间，楼主跑了一俩分钟（maybe）...实在是太久了

            for (int s = 0; s < samples_per_pixel; ++s) {
                double u = (i + random_double()) / (image_width - 1.0);
                double v = (j + random_double()) / (image_height - 1.0);
                ray r = cam.get_ray(u, v);
                pixel_color += ray_color(r, world, max_depth);
            }
            write_color(std::cout, pixel_color, samples_per_pixel);

void write_color(std::ostream &out, color pixel_color, int samples_per_pixel) {
    double r = pixel_color.x();
    double g = pixel_color.y();
    double b = pixel_color.z();

    // Divide the color by the number of samples
    double scale = 1.0 / samples_per_pixel;
    r *= scale;
    g *= scale;
    b *= scale;

    // Write the translated [0,255] value of each color component.
    out << static_cast<int>(256 * clamp(r, 0.0, 0.999)) << \' \'
        << static_cast<int>(256 * clamp(g, 0.0, 0.999)) << \' \'
        << static_cast<int>(256 * clamp(b, 0.0, 0.999)) << \'\\n\';
}

效果

8.2. Using Gamma Correction for Accurate Color Intensity

注意球体下的阴影。 这张照片很暗，但是我们的球体每次反射仅吸收一半的能量，因此它们是50％的反射器。 如果您看不到阴影，请放心，我们将立即修复该阴影。 这些球体看起来应该很亮（在现实生活中为浅灰色）。 这样做的原因是，几乎所有图像查看器都假定图像是经过“伽马校正”的，这意味着0到1的值在存储为字节之前会有一些变换。 这样做有很多充分的理由，但是出于我们的目的，我们只需要意识到这一点。 初步近似，我们可以使用“伽玛2”，这意味着将颜色提升为1 /伽玛的幂，或者在简单的情况下为½（仅平方根）：

void write_color(std::ostream &out, color pixel_color, int samples_per_pixel) {
    auto r = pixel_color.x();
    auto g = pixel_color.y();
    auto b = pixel_color.z();

    // Divide the color by the number of samples and gamma-correct for gamma=2.0.
    auto scale = 1.0 / samples_per_pixel;
    // 此处进行了改动
    r = sqrt(scale * r);
    g = sqrt(scale * g);
    b = sqrt(scale * b);
    
    // Write the translated [0,255] value of each color component.
    out << static_cast<int>(256 * clamp(r, 0.0, 0.999)) << \' \'
        << static_cast<int>(256 * clamp(g, 0.0, 0.999)) << \' \'
        << static_cast<int>(256 * clamp(b, 0.0, 0.999)) << \'\\n\';
}

8.3. Fixing Shadow Acne

There’s also a subtle bug in there. Some of the reflected rays hit the object they are reflecting off of not at exactly t=0t=0, but instead at t=−0.0000001t=−0.0000001 or t=0.00000001t=0.00000001 or whatever floating point approximation the sphere intersector gives us. So we need to ignore hits very near zero:

效果

cpu跑了差不多十几二十分钟...可能是我设置图片是（1600×900）的缘故，看来后续需要改良了

8.4. True Lambertian Reflection

此处介绍的剔除方法会沿表面法线在单位球偏移中生成随机点。 这对应于在半球上接近法线的概率较高的拾取方向，而在掠射角（入射角的余角）处散射射线的概率较低。 此分布按cos3（ϕ）进行缩放，其中ϕ是与法线的夹角。 这是有用的，因为以浅角度到达的光散布在较大的区域上，因此对最终颜色的贡献较小。 但是，我们对具有cos（ϕ）分布的Lambertian分布感兴趣。 True Lambertian射线接近法线散射的可能性更高，但分布更均匀。 这是通过在单位球面的表面上沿表面法线偏移的随机点拾取来实现的。 可以通过在单位球体中选择随机点，然后对其进行规范化来实现在单位球体上选择随机点。

// 单位向量
inline vec3 unit_vector(vec3 v) {
    return v / v.length();
}

vec3 random_unit_vector(){
    return unit_vector(random_in_unit_sphere());
}

Listing 37: [vec3.h] The random_unit_vector() function

This random_unit_vector() is a drop-in replacement for the existing random_in_unit_sphere() function.

if (world.hit(r, 0.001, infinity, rec)) {

改良world.hit函数之后

// 知道取到符合条件的点为止
vec3 random_in_unit_sphere() {
    while (true) {
        vec3 p = vec3::random(-1, 1);
        // 因为圆心是(0,0)，坐标就是表示圆心到随机点的向量
        if (p.length_squared() >= 1)
            continue;
        return p;
    }
}

// 随机后并且归一化
vec3 random_unit_vector(){
    return unit_vector(random_in_unit_sphere());
}

改善随机数的生成法后

鉴于我们两个球的场景是如此简单，因此很难分辨出这两种扩散方法之间的区别，但是您应该能够注意到两个重要的视觉区别：

• 更改后阴影不那么明显
• 更改后，两个球体的外观都较浅

这两个变化都是由于光线的散射更加均匀，朝法线方向散射的光线更少。这意味着，对于漫射物体时，就会出现较轻的 ，因为对相机更多的光线反弹。对于阴影，较少的光直接向上反射，因此较大球体的正下方较小球体的部分更亮。

效果

8.5. An Alternative Diffuse Formulation

为了学习，我们包括了一种直观易懂的扩散方法。对于上述两种方法，我们有一个随机向量，首先是随机长度，然后是单位长度，它从击中点偏移了法线。为何矢量应被法线替换可能并不立即显而易见。

相当于取随机反射向量一定被规定在与法线同向（同一侧），之所以底面阴影减少了，个人理解是在球体底部存在随机后反射向量与法线呈相反方向的情况，与入射向量一样的情况，接着再走射线递归检测，使得函数的递归次数平均会加大，也就是光的能量被吸收的次数平均变大了，也就是阴影会加大，所以在此处减少随机后的反射向量与入射向量同向的情况

vec3 random_in_hemisphere(const vec3& normal){
    vec3 in_unit_sphere = random_in_unit_sphere();

    // In the same hemisphere as the normal
    if (dot(in_unit_sphere, normal) > 0.0)
        return in_unit_sphere;
    else
        return -in_unit_sphere;
}

一种更直观的方法是，在远离击点的所有角度上具有均匀的散射方向，而不依赖于与法线的角度。许多第一批射线追踪论文都使用这种扩散方法（在采用朗伯散射之前）。

// ray recursion
color ray_color(const ray &r, const hittable &world, int depth) {
    hit_record rec;

    // If we\'ve exceeded the ray bounce limit, no more light is gathered.
    if (depth <= 0)
        return color(0, 0, 0);

    // 几何体的颜色
    if (world.hit(r, 0.001, infinity, rec)) {

//        point3 target = rec.p + rec.normal + random_in_unit_sphere();
//        point3 target = rec.p + rec.normal + random_unit_vector();
        // 半球散射的效果
        point3 target = rec.p + random_in_hemisphere(rec.normal);
        return 0.5 * ray_color(ray(rec.p, target - rec.p), world, depth - 1);
    }

    // 背景色
    vec3 unit_direction = unit_vector(r.direction());
    // x y z 映射 r g b
    double t = 0.5 * (unit_direction.y() + 1.0);
    return (1.0 - t) * color(1.0, 1.0, 1.0) + t * color(0.5, 0.7, 1.0);
}

效果

最终效果如下，半球形散射，可以看到底部的阴影相较于之前少很多