数据结构和算法学习笔记三：KMP算法

Posted 2021-05-20 movin2333

一.BF算法

　　KMP算法解决的是字符串匹配的问题。下面首先介绍BF算法：

　　1.最容易想到的字符串匹配的算法：BF（Brute Force，暴力）算法（下面的BF算法图示来自于：http://data.biancheng.net/view/179.html）

　　　　如下图所示：

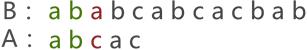
　　　　我们将B字符串称为主串，A字符串称为子串，BF算法或者KMP算法的目的都是计算主串B中是否包含子串A的结果，如果包含，返回主串中的子串出现的第一个字符下标，如果不包含，返回-1(可以称为字符串匹配，很多语言中都有一个indexof方法进行字符串匹配，如C#中string就有IndexOf成员方法）。

　　　　很容易想到，如上图所示，我们将子串的第一个字符和主串第一个字符对齐并逐个字符比较，当主串的第三个字符和子串的第三个字符比较时发现两个字符不同，说明这次匹配失败；接下来将子串右移一位，如下图所示：

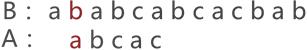
　　　　主串的第二个字符和子串的第一个字符对齐，然后按照对齐顺序还是从第一个字符进行比较，然后发现主串的第二个字符和子串的第一个字符不匹配，这次匹配再次失败；接下来将子串再次右移一位，如下图所示：

　　　　这次主串的第三个字符和子串的第一个字符对齐，然后还是按照对齐顺序进行匹配，发现匹配的子串前四个字符都相同，直到匹配到子串的第五个字符时发现不匹配，这次匹配失败；接下来再次将子串右移一位......重复上述的匹配操作，直到子串移动到如下图所示：

　　　　这次可以发现主串和子串全部相同，匹配成功。

　　2.BF算法总结：

　　　　1）首先将主串和子串对齐，然后按照对齐的位置逐个匹配；

　　　　2）如果对齐的主串和子串全部相同，则匹配成功，否则主串和子串匹配失败；

　　　　3）如果主串和子串匹配失败，则将子串向右移动一位，继续匹配，直到匹配成功或者子串最右端超出主串（如上图中子串第一个字符a和主串的倒数第四个字符c对齐时）；

　　　　4）在子串向右移动一位的过程中其实还包含了匹配位置回溯的操作，如上图中第一次匹配失败时匹配位置是主串第三位和子串第三位，而第二次匹配开始时是主串第二位和子串第一位开始匹配，从主串角度来说，匹配位置从第三位移动到了第二位，从子串角度来说，匹配位置从第三位移动到了第一位，匹配位置都回溯了；

　　　　5）若主串的长度为n，子串的长度为m，在最坏情况下，需要匹配n*m次，因此时间复杂度可以记为O(m*n)。

　　3.代码实现BF算法（C#）（代码只进行了简单的测试，如果您发现了其中的问题可以留言探讨）

      static void Main(string[] args)
      {
          //定义主串
          char[] mainString = {\'a\',\'b\',\'a\',\'b\',\'c\',\'a\',\'b\',\'c\',\'a\',\'c\',\'b\',\'a\',\'b\'};
          //定义子串
          char[] subString = {\'a\',\'b\',\'c\',\'a\',\'c\'};
          //调用方法进行匹配
          Console.WriteLine(BruteForce(mainString,subString));
      }
       
      //暴力匹配的方法
      public static int BruteForce(char[] mainString,char[] subString)
      {
          //主串或子串都不能为空串
          if(mainString.Length == 0 || subString.Length == 0)
          {
              return -1;
          }
          //主串的第几位和子串的第一位对齐
          int mainPosition = 0;
          //当前是子串的第几位和主串匹配
          int subPosition = 0;
          //循环并进行匹配，外层循环条件为子串不超出主串，内层循环依次进行匹配
          //外层循环每次完成后mainPosition变量加1
          while(mainPosition + subString.Length <= mainString.Length)
          {
              for(subPosition = 0;subPosition < subString.Length;subPosition++)
              {
                  //依次匹配主串和子串，如果某次不匹配跳出内层循环，如果匹配到最后一个则返回当前匹配位置
                  if(mainString[mainPosition + subPosition] != subString[subPosition])
                  {
                      break;
                  }
                  else if(subPosition == subString.Length - 1 && mainString[mainPosition + subPosition] == subString[subPosition])
                  {
                      return mainPosition;
                  }
              }
              //一轮匹配不成功则子串右移，重新开始内层for循环时会自动回溯匹配位置
              mainPosition++;
          }
          return -1;
      }

二.KMP算法（The Knuth-Morris-Pratt Algorithm）

　　KMP算法可以理解为BF算法的优化。BF算法的时间复杂度还是较高的，复杂度O(m*n)可以理解为是O(n²)的同阶无穷大，复杂度还是相对较高，KMP算法主要着力于优化BF算法中的一些不必要的比较操作。

　　参考学习资料：「天勤公开课」KMP算法易懂版。

　　1.我们注意到，在BF算法每次匹配失败后，都会有一次回退匹配位置（C语言中这个匹配位置是一个指针，所以经常可以看到回退指针的说法）到子串第一个字符的操作，而KMP算法可以做到不回退匹配位置（对于主串而言），那么KMP算法是如何完成不回退指针的操作呢？考虑到以下几种情况：

　　　　1）注意观察到下面的字符串匹配过程，箭头指向当前匹配位置：

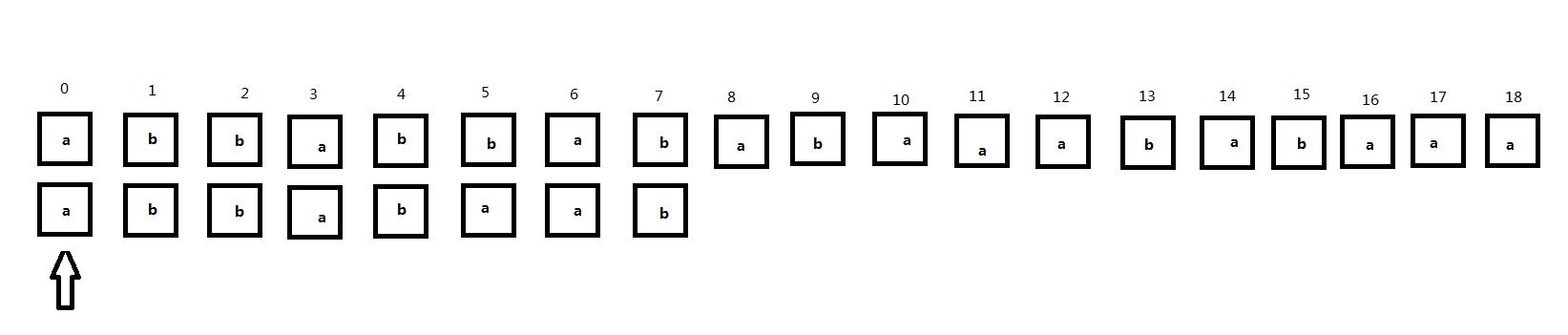
　　　　第一行为主串中字符下标，第二行为主串，第三行为子串。现在从第一位开始匹配，显然当匹配到主串下标为5的字符时出现了不匹配，如下图所示：

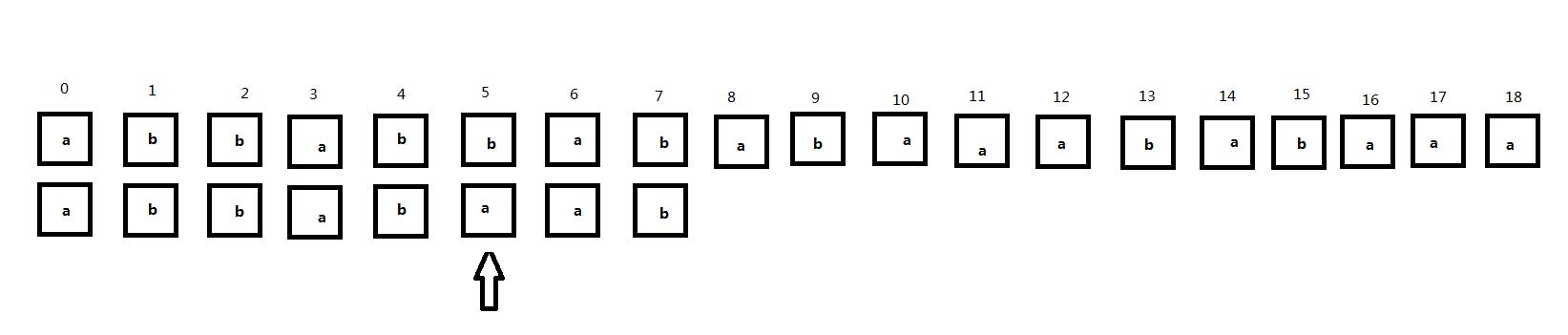
　　　　接下来按照BF算法应该将匹配位置回退到1号位置并将子串右移一位，但是我们可以注意到如下图框选的部分：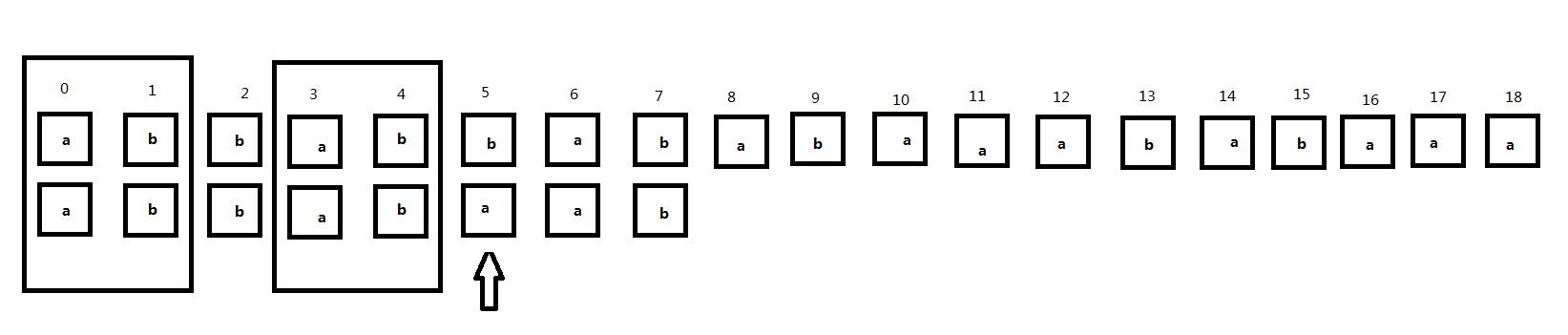

　　　　这里子串中的ab重复出现了两次，那么我们注意第二个框，如下图所示：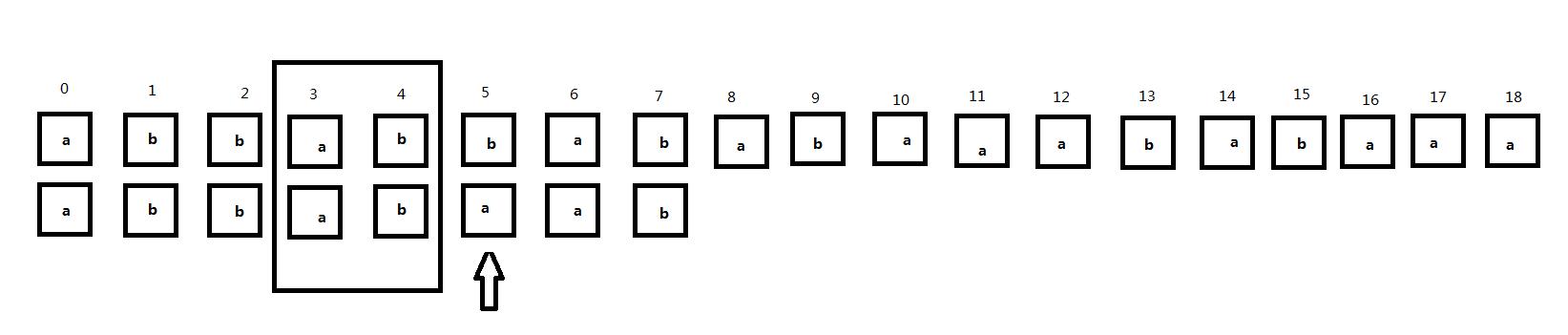

　　　　接下来我们将子串右移，主串是不动的。在子串右移的过程中注意框住的主串3、4位和子串对应位置的匹配情况：

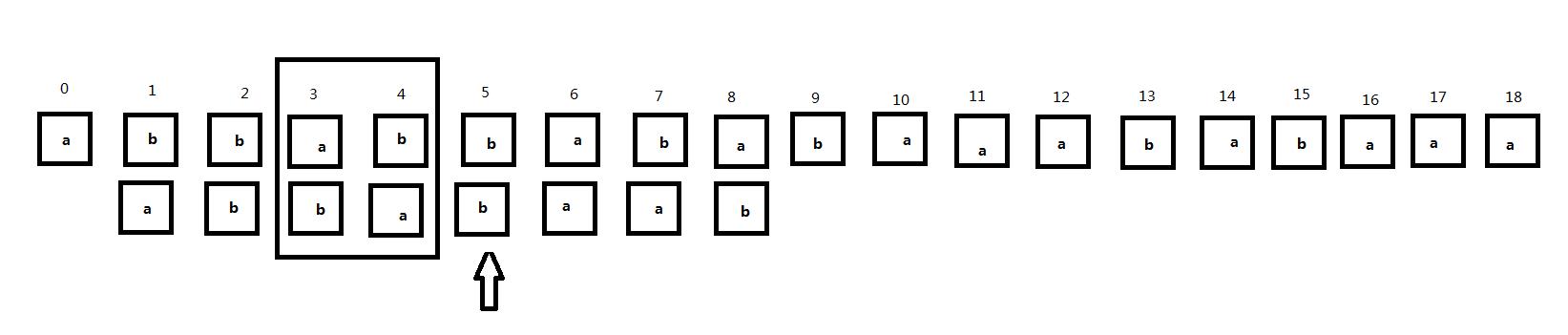
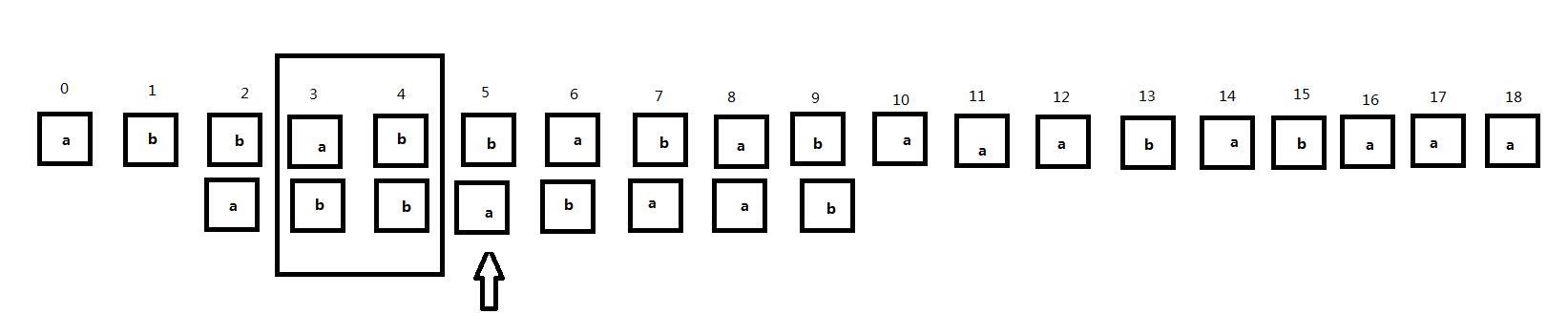
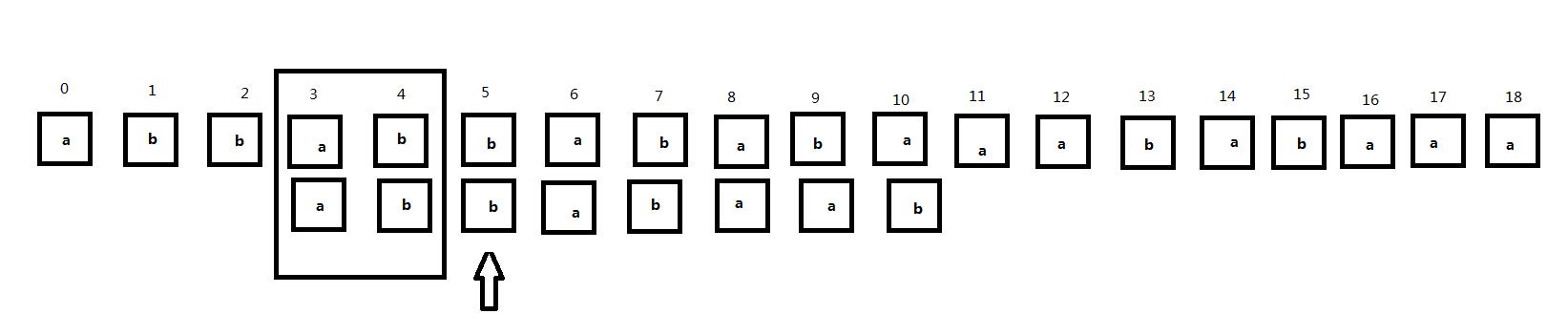
　　　　可以发现，在将子串直接右移的过程中，主串的3、4号位和子串一直不匹配直到子串的0、1号位和主串的3、4号位对齐，原因就在于当我们的匹配位置匹配到5号位发现不匹配的时候，子串中的0、1号位和3、4号位相同，而子串的3、4号位这时和主串的对齐位置是匹配的，所以当子串右移的过程中，子串的其他位置和主串的3、4号位置对齐时肯定不会匹配，直到子串的0、1号位置和主串的3、4号位置对齐，也就是子串中相同的这两部分处于同一位置时。因此，我们可以根据这个原理直接跳过中间的匹配过程而且当前匹配位置（指针位置）不需要回溯。子串中的当前匹配位置前的两个相同的部分我们称为公共前后缀（暂时这样定义）。那么公共前后缀怎么求呢？是只要是子串中相同的部分就可以称为公共前后缀吗？所以我们可以看到接下来的情况。

　　　　2）公共前后缀的找法一

　　　　注意到下面的字符串匹配过程：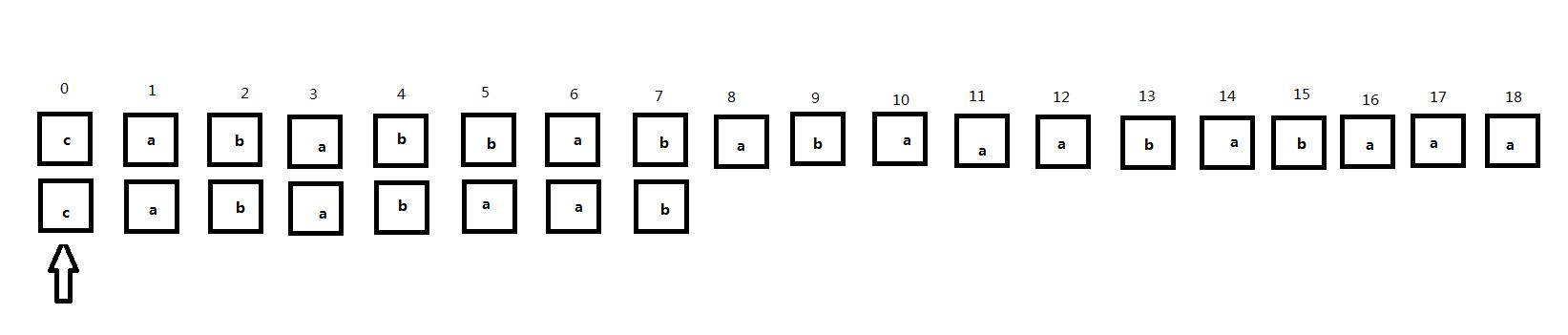

　　　　从头开始匹配字符串。可以注意到同样当匹配到第5位时出现不匹配：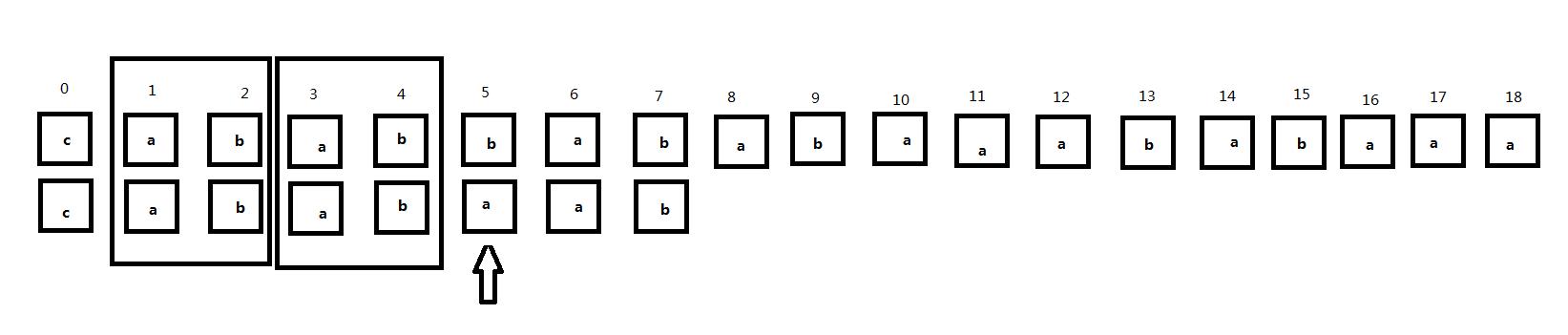

　　　　注意到此时子串匹配位置前的相同部分为1、2位和3、4位。接下来我们将子串向右逐次移动并注意主串3、4位和子串的匹配情况：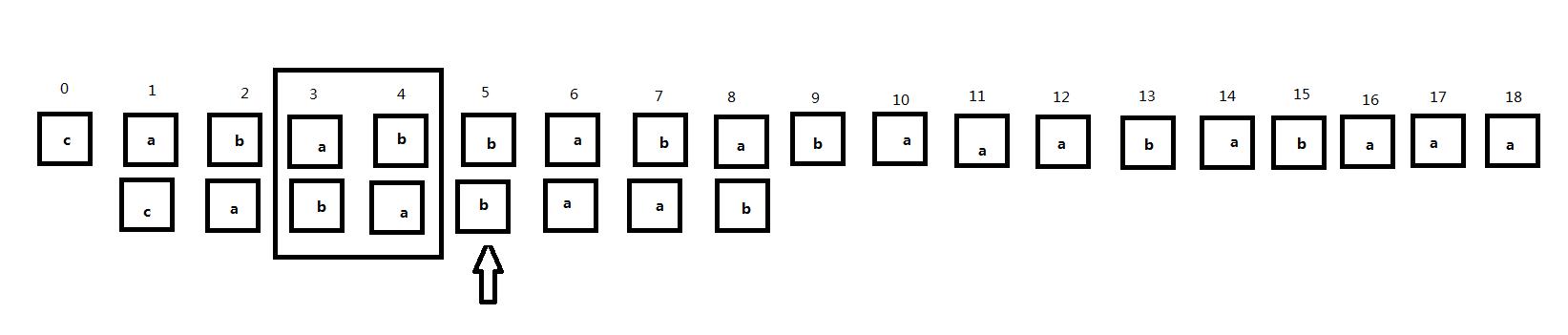

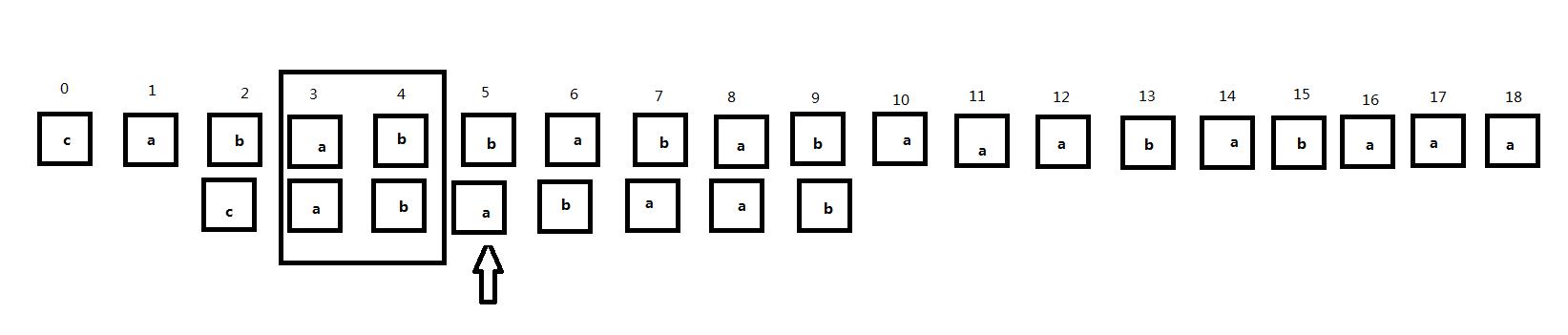
　　　　可以看到子串右移两次后主串3、4号位置就和子串对齐位置匹配了（因为子串的1、2号位置和3、4号位置相同），但是注意到这时子串的0号位对齐主串的2号位，但是这两个位置并不匹配。

　　　　总结：公共前后缀是出现子串和主串不匹配时子串中匹配位置前相同的两部分字符，但是这两个部分中第一部分必须从子串第0位开始看。

　　　　3）公共前后缀的找法二

　　　　同样地，我们注意到下面的匹配过程：

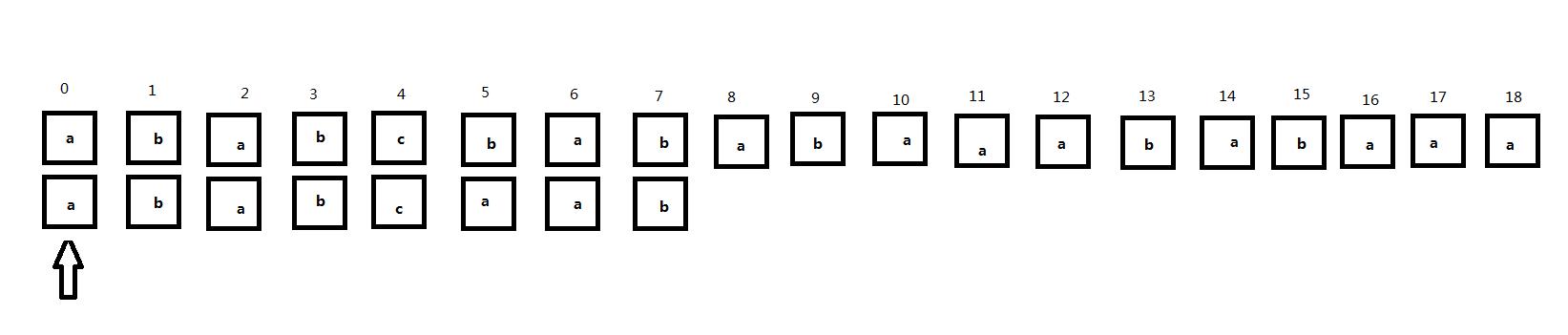
　　　　从头开始匹配，当匹配到主串第5位时出现了不匹配：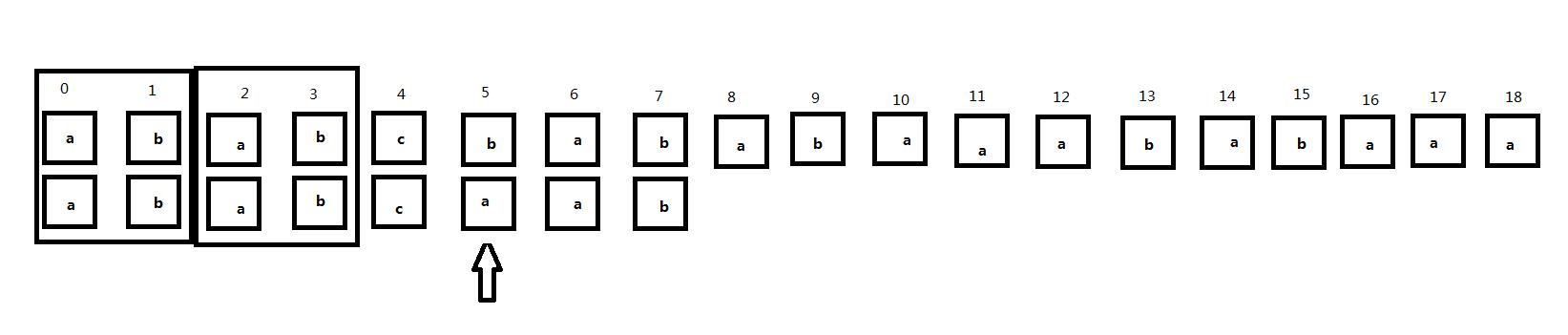

　　　　注意到此时子串中匹配位置前的部分0、1号位置和2、3号位置是相同的，那么我们同样将子串向右移动：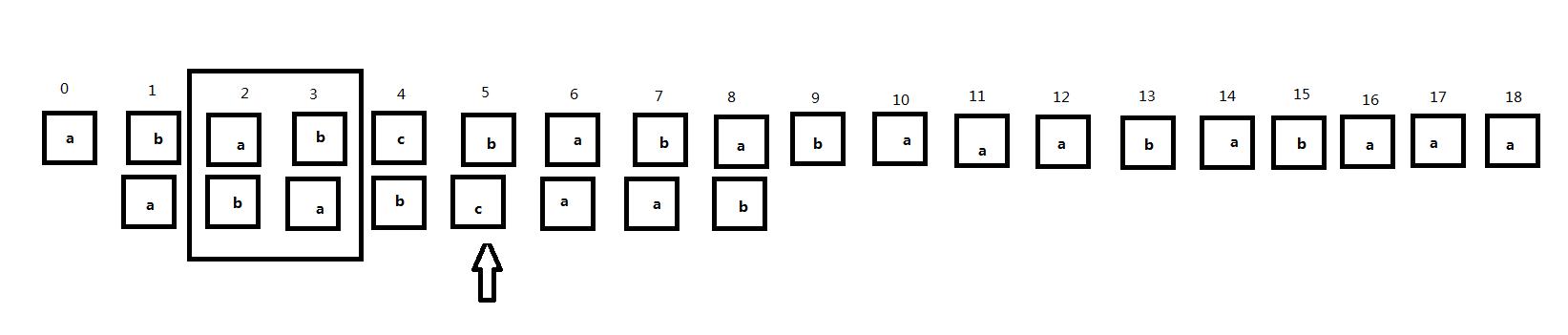

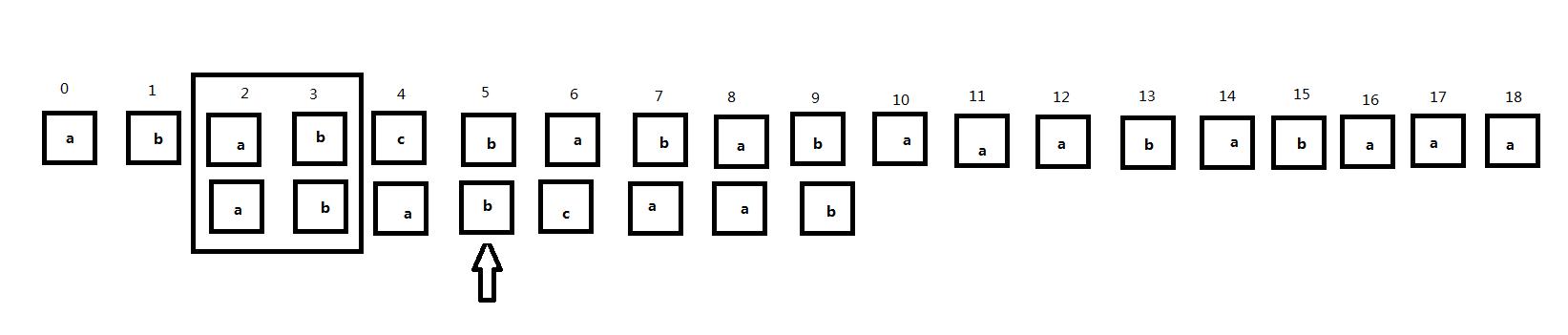
　　　　和刚才的过程类似，当子串向右移动两次后，主串的2、3位和子串再次匹配，但是这时主串的4号位和子串的2号位对齐，但是它们并不匹配。

　　　　总结：公共前后缀是出现子串和主串不匹配时子串中匹配位置前相同的两部分字符，但是这两个部分中第一部分必须从子串第0位开始向右看，第二部分也必须从当前匹配位置左侧位开始向左看。

　　　　4）公共前后缀的找法举例：

　　　　　　从上面的匹配过程中可以看到，公共前后缀只和子串有关，因此我们只看子串。如子串是abbabcda，当不匹配时当前匹配位置是字符c时（5号位），c前面的字符串是abbab，这时看0号位a和4号位b发现不同，再看0、1号位ab和3、4号位ab发现相同，这就是公共前后缀。又如子串是ababaef时，如果当不匹配时当前匹配位置是字符e，e前面的字符串是ababa，这时同样地看0号位a和4号位a发现相同，如果继续看则会发现0、1、2号位aba和2、3、4号位aba也是相同的，这里就出现了两种公共前后缀，对应子串应该右移4格和右移2格，那么该采用哪一种公共前后缀呢？

　　　　5）最大公共前后缀

　　　　　　观察下面的字符串匹配过程：

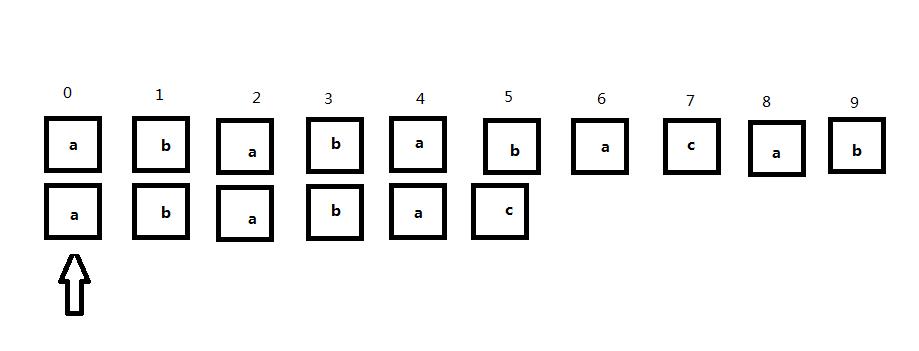
　　　　可以看到当匹配到主串的第5位时出现不匹配，这时子串中当前匹配位置前的部分就是ababa。如果我们采用a作为公共前后缀那么就认为子串在向右移动4位的过程中都不会匹配，因此移动4位后匹配情况如下图所示：

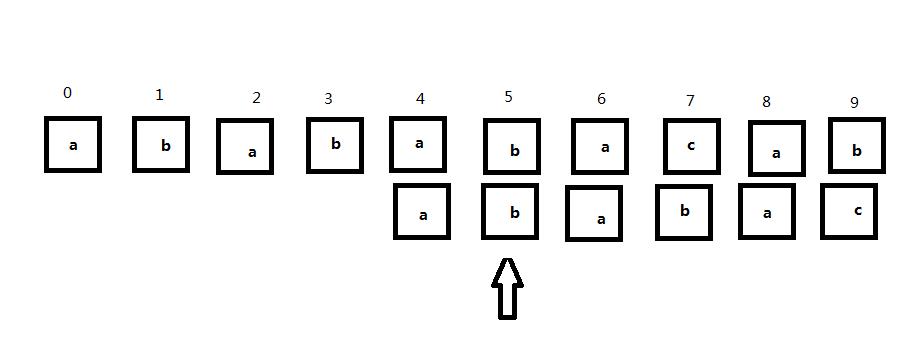
　　　　显然，接下来再匹配，直到第7位发现不匹配，而子串再向右移动就“出头”了，所以最后我们认为子串和主串不能匹配，如下图所示：

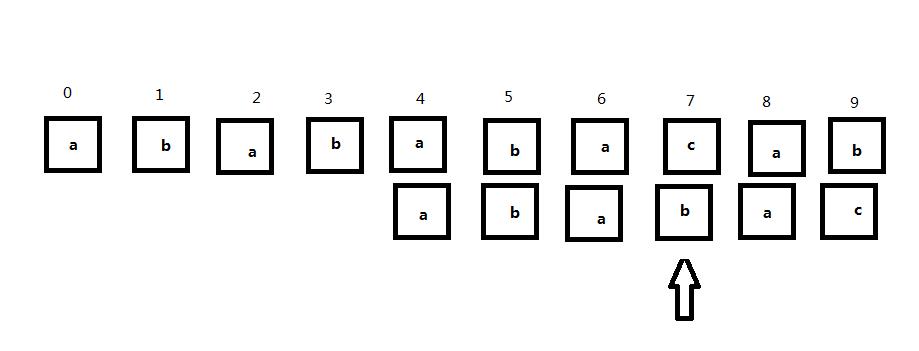
　　　　那么如果我们采用aba作为公共前后缀呢？我们可以认为子串向右移动2位的过程中子串始终和主串始终不匹配，移动后的情况如图所示：

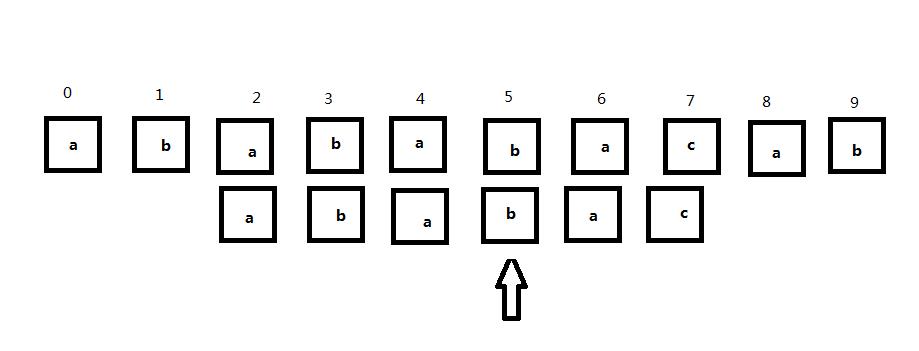
　　　　这时继续向后匹配发现子串和主串完全匹配，那么实际上子串是匹配主串的。

　　　　总结：我们发现当有多个公共前后缀同时出现时，公共前后缀的字符个数越少，子串直接向右移动的步数越多，这时有可能出现遗漏适配的情况，因此我们采用字符个数最多的公共前后缀，这个字符最多的公共前后缀称为最大公共前后缀。

 　　2.next函数值和next数组

　　　　在之前的匹配例子中我们可以看到，当子串和主串出现不匹配时，我们可以不回溯当前匹配的字符位置而只将子串向右直接移动再继续匹配字符，子串向右直接移动的步数取决于当前匹配位置左侧的子串的最大公共前后缀（使得移动前最大公共后缀和移动后最大公共前缀都对齐主串同样的位置，因此这个移动的步数是最大公共前后缀的第一个字符下标差或者最后一个字符下标差）。那么对于一个确定的子串而言，当字符出现不匹配时当前匹配位置指向子串的哪一位和子串中这一位之前字符的组成确定了接下来子串直接向右移动的步数，这个步数和主串的组成情况是无关的。我们可以使用一个函数根据子串的组成和当前匹配位置停留在子串的位置来确定接下来子串向右移动的位数，这个函数就是我们的next函数（next可以理解为指接下来子串向右移动的步数）。

　　　　同时，我们还可以做一个算法上的优化：在匹配的过程中，同样参数的next函数可能运行多次（如子串是abababa，那么可能第一次在子串4号位置a出现不匹配运算一次next函数，下一次子串右移了然后又在子串4号位置出现了不匹配，又运行一次和刚才相同参数的next函数）；我们可以预先根据子串的组成计算不匹配时当前匹配位置停留在子串不同的位置的next函数值（动态规划算法），将其存储起来，这样就避免了next函数的重复运算。我们还可以将这个优化更进一步，当不匹配位置出现在子串的固定位置时，接下来子串向右移动的步数是确定的，那么子串中下一个和主串比较的位置也是固定的（箭头指向子串固定位置，子串再向右移动固定步数，那么移动后箭头指向子串的位置也是固定的），我们可以采用一个数组将这些信息记录下来，数组的下标代表不匹配出现时箭头指向子串的位置，数组值代表子串移动后和主串继续比较的字符位置，这个数组我们称之为next数组。

　　3.总结：KMP算法开始和BF算法相同，都是对齐主串和子串然后逐个比较字符，但是在出现不匹配时的处理方法不相同。KMP算法出现不匹配时不会回溯指针（匹配位置或者图中的箭头），只是将子串向右移动。子串向右移动的步数由最大公共前后缀确定，子串向右移动后再继续从刚才的位置开始比较子串和主串，直到完全匹配或者子串向右移动超出范围。如果主串的字符个数为n，主串的字符个数为m，显然最坏情况为m=1时需要匹配n次，所以这个算法的时间复杂度为O(n)。

　　4.KMP算法的代码实现（C#），参考资料：KMP算法之求next数组代码讲解

        static void Main(string[] args)
        {
            //定义主串
            char[] mainString = { \'a\', \'b\', \'a\', \'b\', \'c\', \'a\', \'b\', \'c\', \'a\', \'c\', \'b\', \'a\', \'b\' };
            //定义子串
            char[] subString = { \'a\', \'b\', \'c\', \'a\', \'c\' };
            //调用方法进行匹配
            Console.WriteLine(KMP(mainString, subString));
            Console.ReadKey();
        }

        //KMP算法
        public static int KMP(char[] mainString, char[] subString)
        {
            //校验参数
            if (mainString.Length == 0 || subString.Length == 0)
            {
                return -1;//返回值-1代表参数不合格或者没有匹配成功
            }
            //得到next数组
            int[] next = GetNextArr(subString);
            //进行逐一匹配
            int point = 0;//记录当前指针（箭头）所在位置
            int cursor = 0;//记录当前和主串指针位置对齐的子串位置(这个位置接下来会进行比较）
            while (point + subString.Length - cursor < mainString.Length)
            {
                //如果成功匹配，指针向右移动
                if (mainString[point] == subString[cursor])
                {
                    point++;
                    cursor++;
                    //如果加1后指针等于字串的字节数，说明加1前指针刚好等于字串字节数减1，那么刚才匹配的就是字串最后一个位置，说明全部匹配
                    if(cursor == subString.Length)
                    {
                        //此时指针指向字串尾部，字串的头部用指针减去字串长度即可
                        return point - subString.Length;
                    }
                }
                //如果没有成功匹配，则需要将子串向右移动
                else
                {
                    cursor = next[cursor];
                    if (cursor == -1)
                    {
                        point++;
                        cursor++;
                    }
                }
            }
            return -1;

        }

        //求解next数组
        public static int[] GetNextArr(char[] subString)
        {
            //创建next空数组
            int[] nextArr = new int[subString.Length];

            //假如当前光标停在n位，求得最大公共前后缀长度为m，那么移动位数为n-m
            //移动后下一个比较的字符为n-(n-m)位，即m位，因此下一个比较的字符就是最大公共前后缀的长度

            //求解最大公共前后缀长度的过程不是很好理解

            //光标位置
            int cursor = -1;
            //指针指向当前求next数组位置的前一位，如当前求next数组中第一位，指针指向0位（因为求next数组和当前指针位置无关，而是和前一位有关）
            int point = 0;
            //next数组的0号位一定赋值-1，代表0号位比较后一定是字串的-1位对准指针（箭头），之后一定是将字串右移一位（右移操作不在这个函数中实现）
            nextArr[point] = cursor;
            //next数组的第一个数字一定是-1，其他数字都根据前一位及之前位去求，所以每个point值进入循环后都实际上给nextArr数组中point+1下标位置赋值
            while (point < nextArr.Length - 1)
            {
                if (cursor == -1 || subString[point] == subString[cursor])
                {
                    cursor++;
                    point++;
                    nextArr[point] = cursor;
                }
                else
                {
                    cursor = nextArr[cursor];
                }
            }

            return nextArr;
        }