二阶贝塞尔曲线 (Bézier Curve)

Posted 2021-05-17 cancantrbl

最近在做签字笔的效果，最初用linerender直接几个点连成一条线的效果并不是很好，特别是当拐弯的时候会有缺口。想要拐弯处变得圆滑起来，决定采用Bezier curve。

定义：起始点、终止点（也称锚点）、控制点。通过调整控制点，贝塞尔曲线的形状会发生变化。

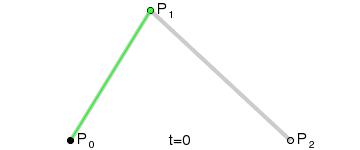
• 由 P0 至 P1 的连续点 Q0，描述一条线段
• 由 P1 至 P2 的连续点 Q1，描述一条线段
• 由 Q0 至 Q1 的连续点 B(t)，描述一条二次贝塞尔曲线

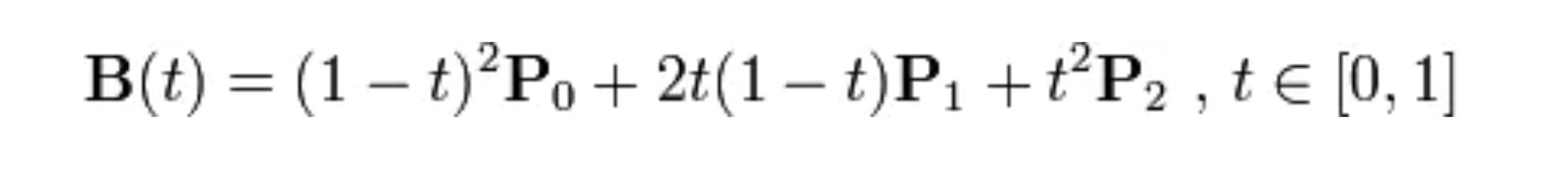
void GetPathPoints(Vector2 controlPoints)
    Vector2[] point = new List<Vector2>()/ /最终贝塞尔曲线上点的集合
    int pointNumber = 5 //贝塞尔曲线上点的数量
    Vector2[] temp_2
    Vector2[] temp_3
    for i = 0, pointNumber - 1 do
        temp_3 = temp_1;
        for j = temp_3.Length - 1, 0, -1 do
            temp_2 = new Vector2[j];
            for k = 0, j do
                temp_2[k] = Vector3.Lerp(temp_3[k], temp_3[k + 1], i / pointNumber)
            end
            temp_3 = temp_2;
        end
        Vector2 find = temp_3
        point.Add(find);
    end
end

 

Reference

1. https://blog.csdn.net/f_957995490/article/details/106571818
2. https://www.jianshu.com/p/afccc4642621