数据结构C语言版 —— 二叉树的顺序存储堆的实现
Posted 爱敲代码的三毛
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构C语言版 —— 二叉树的顺序存储堆的实现相关的知识,希望对你有一定的参考价值。
文章目录
二叉树顺序结构实现(堆)
1. 堆的概念
- 堆在物理上是一个一维数组,在逻辑上是一颗完全二叉树
- 满足父亲节点小于等于孩子节点的叫做小堆或者小根堆
- 满足父亲节点大于等于孩子节点的叫做大堆或者大根堆
堆的孩子和父亲的下标关系
-
已知父亲(parent)的下标
- 左孩子(left)下标等于 l e f t = 2 ∗ p a r e n t + 1 left = 2*parent+1 left=2∗parent+1
- 右孩子(right)下标等于 r i g h t = 2 ∗ p a r e n t + 2 right = 2 * parent + 2 right=2∗parent+2
-
已知左孩子或右孩子下标(child)
- 父亲节点下标等于 p a r e n t = ( c h i l d − 1 ) / 2 parent = (child-1)/2 parent=(child−1)/2

2. 堆的基本操作
堆的向下调整算法
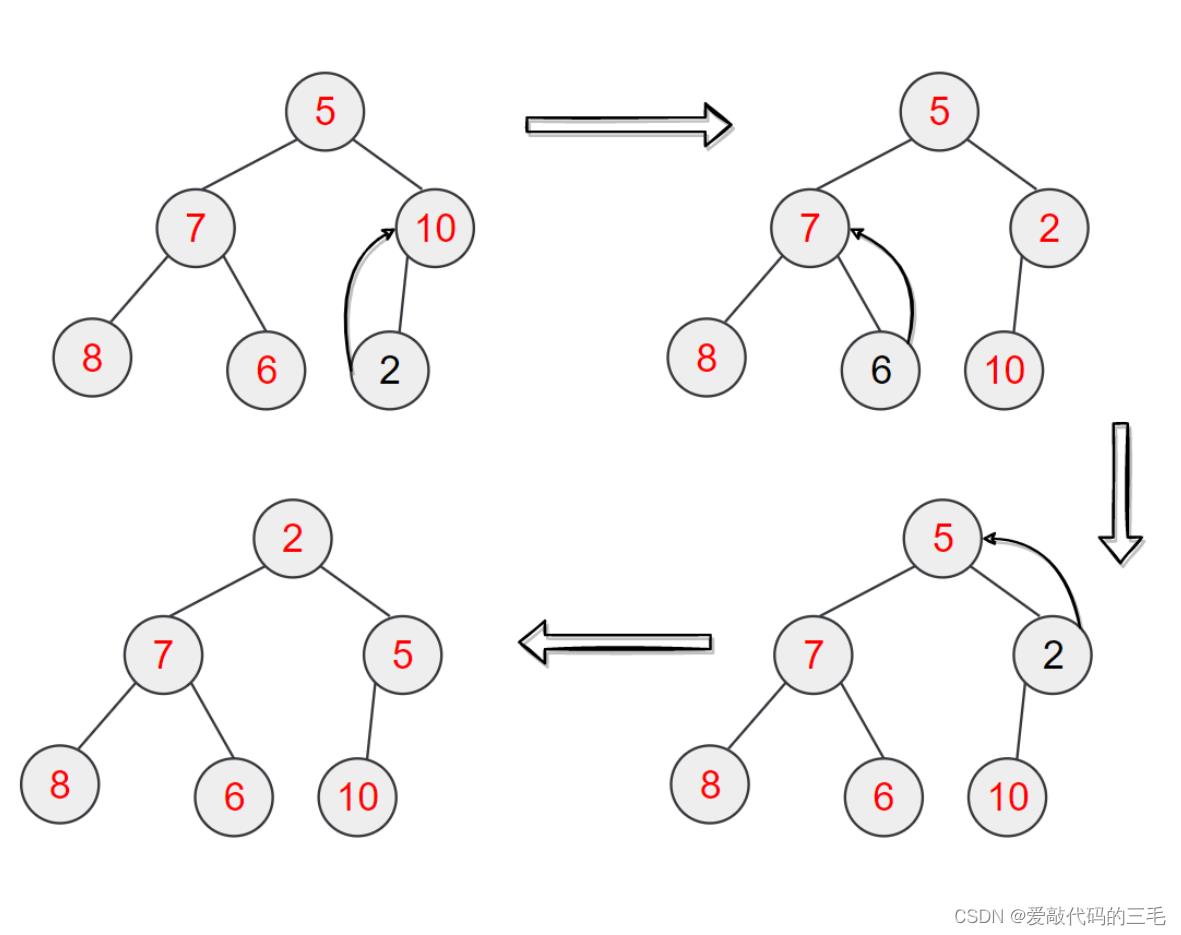
下面这个数组逻辑上可以看作是一棵完全二叉树,通过从根节点开的向下调整算法可以把它调整成一个堆(大堆或小堆),向下调整算法有以有一个前提:左右子树必须是一个堆,才能调整。我这里的是实现小堆的向下调整算法。
建小堆的向下调整的基本思路就是:从堆顶开始,拿自己和较小的一个孩子进行比较大小,如果小就进行交换然后把交换的位置当作父节点继续向下调整,如果两个孩子都比自己小就停止调整,否则一直调整到叶子节点。

// 向下调整(小堆)
void AdjustDown(HPDataType* arr, int n, int index)
int parent = index;
int child = 2 * parent+1;
while (parent < n)
//找出两个孩子里的较小的
if (child < n && child + 1 < n && arr[child] > arr[child + 1])
child++;
// 拿较小的孩子比较和父亲比价大小
if (child < n && arr[child] < arr[parent])
Swap(&arr[child], &arr[parent]);
parent = child;
child = 2 * parent + 1;
else
//说明无需调整
break;
堆的向下调整每次调整的一个节点,假设树的高度为 h h h最坏情况下调整的次数就是 h − 1 h-1 h−1,所以向下调整的时间复杂度就是树的深度 l o g 2 ( n − 1 ) log_2(n-1) log2(n−1),最后得出 l o g 2 n log_2n log2n
堆的创建
我们知道堆的向下调整算法必须满足左右子树都是一个堆,那有的时候是一个普通的数组,也就是一颗普通的完全二叉树,所以要通过建堆来让一个数组变成堆。
建堆的实现思路:从最后一个节点的父节点,也就是第一个非叶子节点的父亲开始不断向下调整,直到整课树都被调整成一个堆。
//向下调整建堆
int i = 0;
//从倒数第一个非叶子节点开始向下调整
for (i = (n - 2) / 2; i >= 0; --i)//n为数组元素个数
AdjustDown(arr,n ,i);
建堆的时间复杂度
我们知道时间复杂度就是计算最坏的时间复杂度,实际上就是计算一个满二叉树,这样每一棵树都会进行调整。
假设这一棵树的高度是 h h h
- 第一层的节点个数就是 2 0 2^0 20、第二层 2 1 2^1 21、第三层 2 2 2^2 22,第 n n n层就有 2 n − 1 2^n-1 2n−1个,那么最后一层就有 2 h − 1 2^h-1 2h−1个节点
- 每一层调整的高度:第一层 h − 1 h-1 h−1、第二层 h − 2 h-2 h−2、…、1
那么假设时间复杂度为 T n T_n Tn,时间复杂度就是从第一层到倒数第二层每个节点的调整次数之和
- 时间复杂度: T ( n ) = 2 0 ∗ ( h − 1 ) + 2 1 ∗ ( h − 2 ) + 2 2 ∗ ( h − 3 ) + 2 3 ∗ ( h − 4 ) + . . . + 2 h − 3 ∗ 2 + 2 h − 2 ∗ 1 T(n) = 2^0*(h-1)+2^1*(h-2)+2^2*(h-3)+2^3*(h-4)+...+2^h-3*2+2^h-2*1 T(n)=20∗(h−1)+21∗(h−2)+22∗(h−3)+23∗(h−4)+...+2h−3∗2+2h−2∗1
- 等式两边同时乘2: 2 ∗ T ( n ) = 2 1 ∗ ( h − 1 ) + 2 2 ∗ ( h − 2 ) + 2 3 ∗ ( h − 3 ) + 2 4 ∗ ( h − 4 ) + . . . + 2 h − 2 ∗ 2 + 2 h − 1 ∗ 1 2*T(n) = 2^1*(h-1)+2^2*(h-2)+2^3*(h-3)+2^4*(h-4)+...+2^h-2*2+2^h-1*1 2∗T(n)=21∗(h−1)+22∗(h−2)+23∗(h−3)+24∗(h−4)+...+2h−2∗2+2h−1∗1
- 使用错位相减法(将上面两个等式进行相减): T ( n ) = 2 1 + 2 2 + 2 3 + 2 4 + . . . + 2 h − 2 + 2 h − 1 − h + 1 T(n) = 2^1+2^2+2^3+2^4+...+2^h-2+2^h-1-h+1 T(n)=21+22+23+24+...+2h−2+2h−1−h+1
- 错位相减后得到一个等比数列: T ( n ) = 2 0 + 2 1 + 2 2 + 2 3 + 2 4 + . . . + 2 h − 2 + 2 h − 1 − h T(n) = 2^0+2^1+2^2+2^3+2^4+...+2^h-2+2^h-1-h T(n)=20+21+22+23+24+...+2h−2+2h−1−h
- 通过等比数列公式$S_n = \\fraca_1(1-q^n)1-q $
- 1 − 2 ( h − 1 ) ∗ 2 1 − 2 \\frac1-2^(h-1)*21-2 1−21−2(h−1)∗2
- T ( n ) = 2 h − 1 − h T(n) = 2^h-1-h T(n)=2