leecode 85 最大矩形 hard

Posted 2021-05-15 AI_Creator

给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。
示例 1：

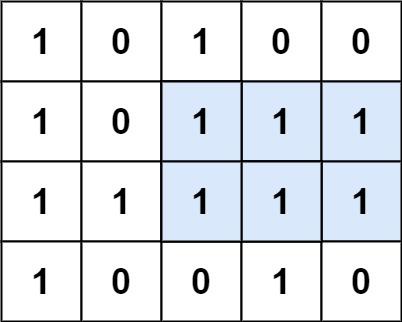
输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：6
解释：最大矩形如上图所示。
示例 2：

输入：matrix = []
输出：0
示例 3：

输入：matrix = [["0"]]
输出：0
示例 4：

输入：matrix = [["1"]]
输出：1
示例 5：

输入：matrix = [["0","0"]]
输出：0

提示：

rows == matrix.length
cols == matrix[0].length
0 <= row, cols <= 200
matrix[i][j] 为 \'0\' 或 \'1\'

暴力解法

暴力解法的思路参考
https://leetcode-cn.com/problems/maximal-rectangle/solution/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-by-1-8/

  public int maximalRectangle(char[][] matrix)
    {
        if(matrix.length==0) return 0;
        int maxArea=0;
        int[][] new_maxtrix= new int[matrix.length][matrix[0].length];
        for(int i=0;i<new_maxtrix.length;i++)
        {
            for(int j=0;j<new_maxtrix[0].length;j++)
            {
                if(matrix[i][j]==\'1\')
                {
                    if(j==0)
                    {
                     new_maxtrix[i][j]=1;
                    }else {
                        new_maxtrix[i][j] = new_maxtrix[i][j - 1] + 1;
                    }
                }else
                {
                    new_maxtrix[i][j]=0;
                }

                int minwidth=new_maxtrix[i][j];
                int height;
                for(int k=i;k>=0;k--)
                {
                    height=i-k+1;
                    minwidth=Math.min(minwidth,new_maxtrix[k][j]);
                    maxArea=Math.max(maxArea,minwidth*height);
                }
            }
        }
    return maxArea;
    }

单调栈

解题思路
https://www.cnblogs.com/AI-Creator/p/14767387.html

 public int compute(int[][] arr,int row)
    {
        int ans=0;
        LinkedList<Integer> stack= new LinkedList<>();
        //每一行单调递增栈
        int l,r;
        for(int i=0;i<arr[0].length;i++)
        {
            while (!stack.isEmpty()&&arr[row][i]<arr[row][stack.peek()])
            {
                int curr=stack.pop();
                l=stack.peek();
                r=i;
                ans= Math.max(ans,(r-l-1)*arr[row][curr]);
            }
            stack.push(i);
        }
        return ans;
    }


    public int maximalRectangle(char[][] matrix) {
        if(matrix.length==0) return 0;
        int[][] height_matrix = new int[matrix.length][matrix[0].length+2];
        //构造高度矩阵
        for(int i=1;i<height_matrix[0].length-1;i++)
        {
            height_matrix[0][i]=matrix[0][i-1]-\'0\';
        }

        for(int i=1;i<height_matrix.length;i++)
        {
            for(int j=1;j<height_matrix[0].length-1;j++)
            {
                if(matrix[i][j-1]==\'0\')continue;
                height_matrix[i][j]=height_matrix[i-1][j]+1;
            }
        }
        int max= 0;
        for(int i=0;i<height_matrix.length;i++)
        {
            max=Math.max(compute(height_matrix,i),max);
            int a=5;
        }

        return max;

    }

动态规划？