[计数dp] 整数划分(模板题+计数dp+完全背包变种题)
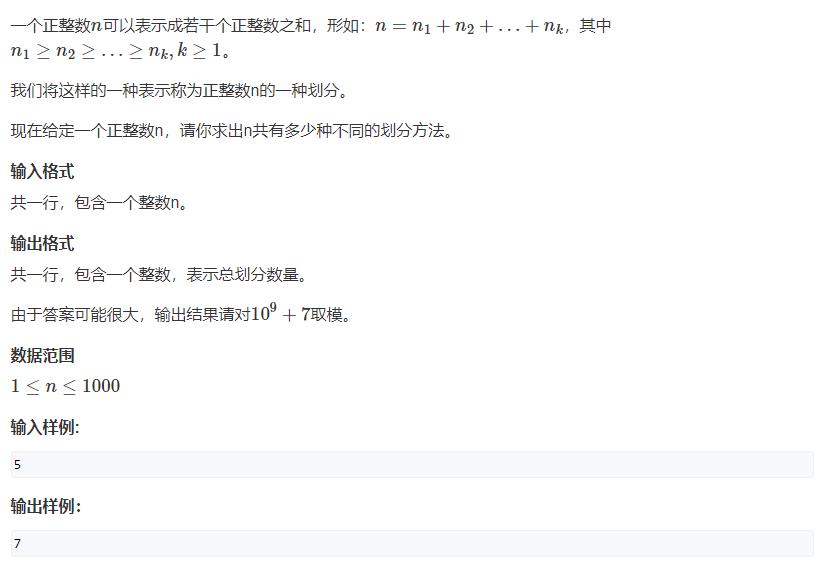
Posted tags: 篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了[计数dp] 整数划分(模板题+计数dp+完全背包变种题)相关的知识，希望对你有一定的参考价值。 计数类 dp 可分为 计数 dp 和数位统计 dp。大多是用来统计方案数什么的，特别强调 不重不漏，在此还是根据各个题的特点将计数 dp 和数位 dp 分开整理。其实数位 dp 的题目会相对多很多… AcWing 900.整数划分 重点： 计数 dp、完全背包问题抽象 首先模拟下样例便于理解本题： 故我们可以将问题抽象为一个容量为 n 的背包，有 n 个体积为 1 ~ n 的物品，求恰好将该背包的方案数。每种物品可以使用无限次，故该问题是一个完全背包问题。 思路： 完全背包代码： 除了完全背包的写法及状态定义外，也有一种其它的状态定义方式，状态转移方程不同但是却能得到相同的结果… 思路： 代码： 故可看出，同一个 dp 问题，不同的思考方式，不同的集合划分，不同的状态转移方程，只有思路是正确的，那么就是可行的。当然，在本题，划分方式不同导致了状态转移方程的不同，进而导致了求解答案时也不同。 以上是关于[计数dp] 整数划分(模板题+计数dp+完全背包变种题)的主要内容，如果未能解决你的问题，请参考以下文章 POJ 2229 sumset ( 完全背包 || 规律递推DP )计数dp 模板题
5 = 5
= 4 + 1
= 3 + 2
= 3 + 1 + 1
= 2 + 1 + 1 + 1
= 2 + 2 + 1
= 1 + 1 + 1 + 1 + 1
共七种划分方式
f[i][j]：从 1~i 中选，且总体积恰好为 j 的选法数量
f[i-1][j]f[i-1][j - i]f[i-1][j - 2*i]f[i-1][j - s*i]
f[i][j] = f[i-1][j]+f[i-1][j-1]+f[i-1][j-i*2]+...+f[i-1][j-i*s]f[i][j-i] = f[i-1][j-i]+f[i-1][j-i*2] +..+ f[i-1][j-i*s]f[i][j] = f[i-1][j] + f[i][j-i]f[i][j]=f[i-1][j]+f[i][j-i]const int mod = 1e9 + 7;
void solve() {
int n;
cin >> n;
int f[n + 1] = {1};
for (int i = 1; i <= n; ++i)
for (int j = i; j <= n; ++j)
f[j] = (f[j] + f[j - i]) % mod;
cout << f[n] << endl;
}
f[i][j] ：所有总和是 i，并且恰好表示成 j 个数的和的方案的数量
f[i-1][j-1]，等价于和是 i-1 数量是 j-1 的选法数量f[i][j] = f[i-1][j-1]+f[i-j][j]ans = f[n][1] + f[n][2] +...+f[n][n]f[0][0] = 1 代表总和是 0 的时候选 0 个的方案数是 1const int mod = 1e9 + 7;
const int N = 1e3 + 10;
int f[N][N];
void solve() {
int n;
cin >> n, f[0][0] = 1;
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= i; ++j)
f[i][j] = (f[i - 1][j - 1] + f[i - j][j]) % mod;
int ans = 0;
for (int i = 1; i <= n; ++i)ans = (ans + f[n][i]) % mod;
cout << ans << endl;
}
参考