树形选择排序(锦标赛排序)

Posted 2021-05-12 Acx7

介绍：

　　树形选择排序(Tree Selection Sort)，又称锦标赛排序(Tournament Sort)，是一种按锦标赛的思想进行选择排序的方法。简单选择排序花费的时间主要在比较上，每次都会进行很多重复的比较，造成浪费时间。锦标赛排序就是通过记录比较结果，减少比较次数，从而降低时间复杂度。

算法描述：

　　首先对n个记录的关键字进行两两比较，然后再对胜者进行两两比较，如此重复，直至选出最小关键字的记录为止。这个过程可用一棵有n个叶子结点的完全二叉树描述。

图片演示：

　　用锦标赛排序对下图序列排序。

　　　两两比较构造完全二叉树。

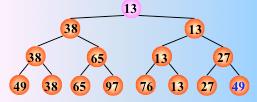
　　 选出最小值，并修改该叶节点关键字为∞。

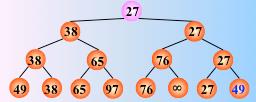
　　 重复上述过程，直至叶节点全为∞，排序完成。

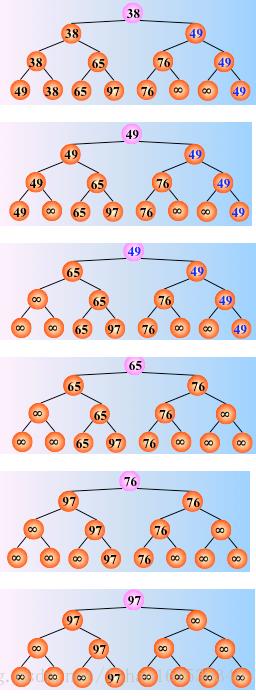
性能分析：

　　时间复杂度：O(NlogN)

　　空间复杂度：O(N)

　　稳定性：不稳定

　　缺点：辅助存储空间较多，和∞的比较多余。

　　为了弥补这些缺点，威洛姆斯(J·willioms)在1964年提出了另一种形式的选择排序——堆排序。

代码实现：

// Java代码
class TreeSelectionSort {
    public static void treeSelectionSort(int[] data) {
        //长度小于2，无需排序
        if(data.length<2){
            return;
        }
        
        int leafCount = 1;    //满二叉树的叶子节点数，非完全二叉树叶子节点数
        //计算出满二叉树的叶子节点数，节点数大于等于数据队列的长度
        while (leafCount < data.length) {
            leafCount *= 2;
        }

        int[] tree = new int[leafCount * 2];  //树，tree[0]不存储数据
        //data里面的值赋值到树叶子节点
        for (int i = 0; i < data.length; i++) {
            tree[tree.length - i - 1] = data[i];
        }
        //初始化还没有赋值的树叶子结点，赋值叶子节点最小值
        for (int i = data.length; i < leafCount; i++) {
            tree[tree.length - i - 1] = Integer.MIN_VALUE;
        }

        //初始化，构建整棵树
        for (int i = tree.length - 1; i > 1; i -= 2) {
            tree[i / 2] = Math.max(tree[i], tree[i - 1]);
        }
        data[data.length-1] = tree[1];   //将树根节点赋值于data
        
        int maxIndex;   //堆最大值所对应的叶子节点的下标
        //继续寻找剩下的最大值，逆向存储，升序排序
        for (int i = data.length-2; i >=0; i--) {
   
            maxIndex = tree.length - 1;  //默认堆最后一个位置
            //寻找树根值所在的叶子节点的位置
            while (tree[maxIndex] != tree[1]) {
                maxIndex--;
            }
            tree[maxIndex]=Integer.MIN_VALUE; //该叶子节点赋值最小值
            
            //调整树，根节点值最大
           while(maxIndex>1){
                //左叶子结点
                if (maxIndex % 2 == 0) {
                    tree[maxIndex / 2] = Math.max(tree[maxIndex] ,
                              tree[maxIndex + 1]);
                } else {
                    tree[maxIndex / 2] = Math.max(tree[maxIndex] ,
                              tree[maxIndex - 1]);
                }
                maxIndex/=2;//指向父节点
            }

            data[i] = tree[1];   //将树根节点赋值于data
        }
    }
}

算法优化：

　　上面代码一次遍历只是找出未排序序列中的最小值，其实我们可以在遍历过程中同时找出最小值和最大值，并把每次找出的最大值按顺序放到每次排列数据的末尾。时间复杂度还是 O(N^2) ，只相对前面的减少了一半遍历次数。