二叉排序树

Posted 2021-05-11 撑起一片阳光

二叉排序树

1.二叉排序树的介绍

二叉排序树：BTS（Binary Sort Tree）,对于二叉排序树的任何一个非叶子节点，要求左子节点的值小于当前节点的值，右子节点的值大于当前结点的值。如果有相同值，可以将该结点放到左边或右边。

比如：{7，3，10，12，5，1，9}

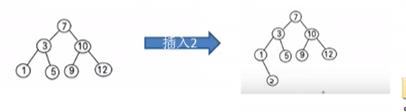
2.排序二叉树的新增
思路：若树为空，则直接插入。
比较插入结点值和当前结点的值大小，如果插入值小。
判断当前节点的左子节点是否为空，如果为空直接插入，不为空，向左递归。
如果插入值大，判断右子节点是否为空，如果为空直接插入，不为空，向右递归。

3.排序二叉树的删除有三种情况

1）删除叶子节点（比如：2，5，9，12）；

思路：①需要找到要删除的结点node,然后再找到node的父节点parentNode.

​ ②判断node时parentNode的左子节点还是右子节点，

​ 左子节点： parentNode.left = null;

​ 右子节点： parentNode.right = null;

2）删除只有一棵树的叶子节点；

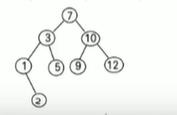
思路：①需要找到要删除的结点node,然后再找到node的父节点parentNode.

​ ② 判断node存在左子节还是右子节点

​ ③判断node是parentNode左子节点还是右子节点

​ 1.如果node有左子节点 .

​ 1.1 node是parentNode的左子节点

​ parentNode.left = node.left

​ 1.2 node是parentNode的左子节点

​ parentNode.right = node.left

​ 2.如果node有右子节点

​ 1.1 node是parentNode的左子节点

​ parentNode.left = node.right

​ 1.2 node是parentNode的左子节点

​ parentNode.right = node.right

3）删除只有两棵树的叶子节点；

思路：①需要找到要删除的结点node,然后再找到node的父节点parentNode.

​ ②从node的右子树找到最小的结点。

​ ③用临时变量将最小结点存储，然后删除最小节点。

​ ④然后将该值赋给要删除的结点。

package com.sratct.tree;

import java.util.LinkedList;
import java.util.logging.Level;

/**
 * 二叉排序树
 */
public class BinaryTreeDemo1 {
    public static void main(String[] args) {
        int[] arr = {7, 3, 10, 12, 5, 1, 9, 2};
        BNode bNode = new BNode(arr[0]);
        for (int i = 1; i < arr.length; i++) {
            add(bNode, new BNode(arr[i]));
        }
        delNode(bNode,7);
        zList(bNode);
    }

    // 添加结点
    public static void add(BNode root, BNode node) {
        if (node == null) {
            return;
        }
        if (root == null) {
            root = node;
            return;
        }
        // 判断插入结点的和当前结点的大小
        if (node.no < root.no) {
            // 小于，判断左子节点是否为空
            if (root.left == null) {
                root.left = node;
            } else {
                add(root.left, node);
            }
        } else {
            // 大于，判断右子节是否为空
            if (root.right == null) {
                root.right = node;
            } else {
                add(root.right, node);
            }
        }
    }

    // 层序遍历
    public static void zList(BNode root) {
        LinkedList<BNode> bNodes = new LinkedList<>();
        if (root == null) {
            return;
        }
        bNodes.offer(root);
        while (!bNodes.isEmpty()) {
            BNode poll = bNodes.poll();
            System.out.println(poll.no);
            if (poll.left != null) {
                bNodes.offer(poll.left);
            }
            if (poll.right != null) {
                bNodes.offer(poll.right);
            }
        }
    }

    // 删除结点
    public static void delNode(BNode root, int value) {
        if (root == null) { // 如果树为空，直接返回
            return;
        } else {
            // 查找要删除的结点
            BNode node = searchNode(root, value);
            if (node == null) { // 如果为空，则没找到要删除的结点
                return;
            }
            // 如果找到该节点，但是根节点的左右子节点都为空，则要删除的为根节点，且此树只有一个结点
            if (root.left == null && root.right == null) {
                root = null;
                return;
            }
            // 查找要删除结点的父节点
            BNode parentNode = searchParentNode(root, value);
            // 1. 删除的结点为叶子节点
            if (node.left == null && node.right == null) { // 为叶子节点
                // 判断该节点是父节点的左子节点还是右子节点
                if (parentNode.left != null && parentNode.left.no == value) {
                       // 为左子节点
                    parentNode.left = null;
                } else  {
                    parentNode.right = null;
                }
            } else if (node.left != null && node.right != null) { // 3.删除只有两棵树的叶子节点；
                int temp = minNode(node.right); //找到最小值
                node.no = temp;
            } else { // 2.删除只有一棵树的叶子节点；
                // 判断node是否存在左子节点
                if (node.left != null) {
                    // node存在左子节点，判断node是parentNode的左子节点还是右子节点
                    if (parentNode.left.no == value) {
                        //node是parentNode的左子节点
                        parentNode.left = node.left;
                    } else {
                        // node是parentNode的右子节点
                        parentNode.right = node.left;
                    }
                } else {
                    // node存在右子节点,判断node是parentNode的左子节点还是右子节点
                    if (parentNode.left.no == node.no) {
                        //node是parentNode的左子节点
                        parentNode.left = node.right;
                    } else {
                        parentNode.right = node.right;
                    }
                }
            }
        }
    }

    /**
     * 以node为根节点的二叉排序树
     * 找到node的左子树上最小结点返回且删除该节点
     * @param node
     * @return
     */
    public static int minNode(BNode node) {
        BNode temp = node;
        while (temp.left != null) {
            temp = temp.left; // 一直找到右子树上最小的那个结点
        }
        delNode(node, temp.no); // 并删除该节点
        return temp.no;
    }
    // 查找要删除的结点
    public static BNode searchNode(BNode root, int value) {
            if (value == root.no) { // 如果相等，则找到返回
                return root;
            } else if (value < root.no) {  // 如果小于当前结点的值，左递归
                if (root.left == null) {
                    return null;
                }
               return searchNode(root.left, value);
            } else {  // 如果大于当前结点的值，右递归
                if (root.right == null) {
                    return null;
                }
                return searchNode(root.right, value);
            }
    }

    // 查找要删除结点的父节点
    public static BNode searchParentNode(BNode root, int value) {
        // 如果当前节点的左子节点不为空，且左子节点的值等于要删除的值则当前节点为父节点
        //如果当前节点的右子节点不为空，且右子节点的值等于要删除的值则当前节点为父节点
        if ((root.left != null && root.left.no == value) || (root.right != null && root.right.no == value)) {
            return root;
        } else if (root.no > value && root.left != null) { // 如果当前结点的值大于要删除的结点 且 当前节点的左子节点不为空，左递归
            return searchParentNode(root.left, value);
        } else if (root.no < value && root.right != null) {// 如果当前结点的值小于要删除的结点 且 当前节点的右子节点不为空，右递归
            return searchParentNode(root.right, value);
        } else {
            return null;
        }
    }
}

class BNode {
    public int no;
    public BNode left;
    public BNode right;

    public BNode(int no) {
        this.no = no;
    }
}