leetcode-158周赛-5224-掷筛子模拟

Posted 2021-03-26 真不知道叫啥好

题目描述：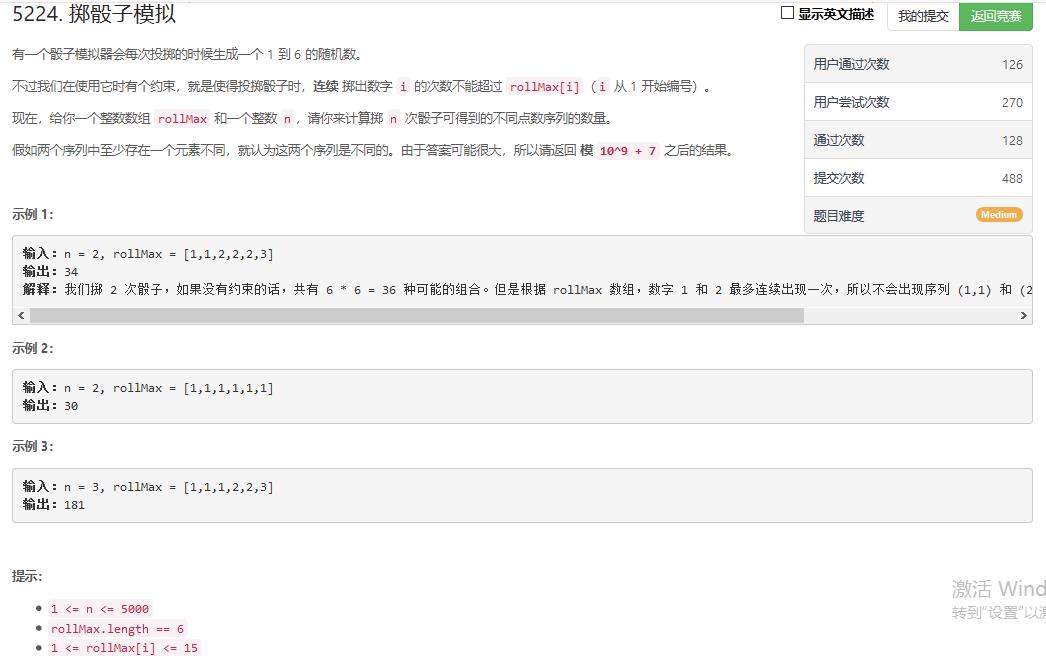

 

 方法：动态规划O(6∗6∗n∗15)

递归：

from functools import lru_cache
class Solution:
    def dieSimulator(self, n, rollMax):
        MOD = 10 ** 9 + 7
        @lru_cache(None)
        def dp(i, j, k):
            # i rolls, recently rolled j, k times
            if i == 0:
                return 1
            ans = 0
            for d in range(6):
                if d != j:
                    ans += dp(i-1, d, 1)
                elif k + 1 <= rollMax[d]:
                    ans += dp(i-1, d, k+1)
            ans %= MOD
            return ans
        return dp(n, -1, 0) % MOD

迭代：

class Solution(object):
    def dieSimulator(self, n, rollMax):
        M = 10**9+7
        data = [[1]+[0]*(rollMax[i]-1) for i in range(6)]
        for _ in range(n-1):
            sums = [sum(x) for x in data]
            s = sum(sums)
            for j in range(6):
                n = rollMax[j]
                for k in range(n-1,0,-1):
                    data[j][k] = data[j][k-1]
                data[j][0] = (s - sums[j]) % M
            #print (data)
        return sum([sum(x) for x in data]) % M

解析：

 

 

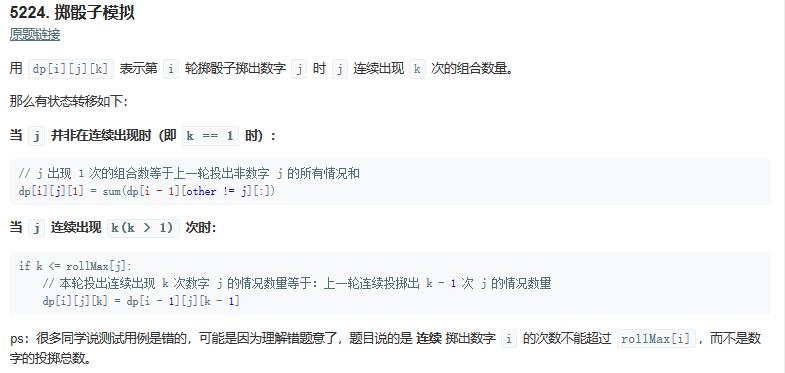
class Solution:
    def dieSimulator(self, n: int, rollMax: List[int]) -> int:
        dp = [[[0 for _ in range(16)] for _ in range(7)] for _ in range(n + 1)]
        mod = 10**9 + 7
                
        for i in range(1, n + 1):
            # 投掷的数
            for j in range(1, 7):
                # 第一次投掷
                if i == 1:
                    dp[i][j][1] = 1
                    continue
                
                # 数字 j 连续出现 k 次
                for k in range(2, rollMax[j - 1] + 1):
                    dp[i][j][k] = dp[i - 1][j][k - 1]
                    
                # 前一次投出的数不是 j
                s = 0
                for l in range(1, 7):
                    if l == j:
                        continue
                    for k in range(1, 16):
                        s += dp[i - 1][l][k]
                        s %= mod
                dp[i][j][1] = s
        
        res = 0
        for j in range(1, 7):
            for k in range(1, 16):
                # 求投掷 n 次时所有组合总和
                res += dp[n][j][k]
                res %= mod
                
        return res