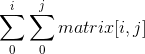Baozi Leetcode solution 1292. Maximum Side Length of a Square with Sum Less than or Equal to Th

Posted 2021-03-22 baozitraining

Problem Statement 

Given a m x n matrix mat and an integer threshold. Return the maximum side-length of a square with a sum less than or equal to threshold or return 0 if there is no such square.

 

Example 1:

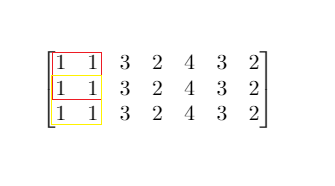
Input: mat = [[1,1,3,2,4,3,2],[1,1,3,2,4,3,2],[1,1,3,2,4,3,2]], threshold = 4
Output: 2
Explanation: The maximum side length of square with sum less than 4 is 2 as shown.

Example 2:

Input: mat = [[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2]], threshold = 1
Output: 0

Example 3:

Input: mat = [[1,1,1,1],[1,0,0,0],[1,0,0,0],[1,0,0,0]], threshold = 6
Output: 3

Example 4:

Input: mat = [[18,70],[61,1],[25,85],[14,40],[11,96],[97,96],[63,45]], threshold = 40184
Output: 2

 

Constraints:

• 1 <= m, n <= 300
• m == mat.length
• n == mat[i].length
• 0 <= mat[i][j] <= 10000
• 0 <= threshold <= 10^5

 Problem link

Video Tutorial

You can find the detailed video tutorial here

• Youtube
• B站

Thought Process

There is an absolute brute force way is to calculate the sum of each square in every iteration. There are previous similar problems that we can have a prefix sum matrix, similar to the rolling sum idea on one dimensional array.

 

A prefix sum matrix is a matrix that for each cell[i, j] represents the sum in original matrix from matrix[0, 0] to matrix [i, j] (inclusive)

 

The advantage is later we can get any rectangle sum simply performing below

 

sum from [i, j] to [i + len][j + len] = prefixSum[i + len][j + len] - prefixSum[i - 1][j + len] - prefixSum[i + len][j - 1] + prefixSum[i - 1][j - 1]

Two more optimizations we can do

• We can apply binary search instead of a linear one to find the max length
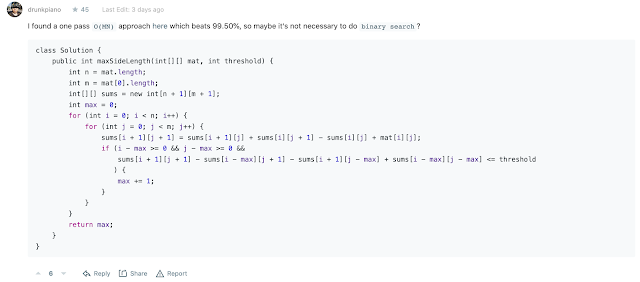
• We can also keep a record of the sum while building up the prefix sum matrix. The reason this works is if it has a square say 3x3 that meets the requirement, then it would definitely have a square 2x2 meet the requirement. So we can start from 1x1, 2x2 till we reach the max. Pretty smart! Kudos to @drunkpiano

 

 

• Reference is here: Leetcode discussion solution with binary search and smart solution

Solutions

 

 1 public int maxSideLength(int[][] mat, int threshold) {
 2     if (mat == null || mat.length == 0 || mat[0].length == 0) {
 3         return 0;
 4     }
 5     int row = mat.length;
 6     int col = mat[0].length;
 7     // easier to implement with the initial value on the boarder to be 0
 8     int[][] prefixSum = new int[row + 1][col + 1];  
 9 
10     // the idea of using a prefix sum matrix should be a common technique, each cell contains the sum of
11     // its top left sum, including itself
12     for (int i = 1; i <= row; i++) {
13         for (int j = 1; j <= col; j++) {
14             prefixSum[i][j] = prefixSum[i - 1][j] + prefixSum[i][j - 1] - prefixSum[i - 1][j - 1] + mat[i - 1][j - 1]; // needs to plus itself as well
15         }
16     }
17 
18     // brute force way to start from max length O(M*N*min(M, N))= O(N^3)
19     // could use binary search to find the first element
20     // https://leetcode.com/problems/maximum-side-length-of-a-square-with-sum-less-than-or-equal-to-threshold/discuss/451871/Java-sum%2Bbinary-O(m*n*log(min(mn)))-or-sum%2Bsliding-window-O(m*n)
21     for (int len = Math.min(row, col); len >= 1; len--) {
22         for (int i = 1; i + len <= row; i++) {
23             for (int j = 1; j + len <= col; j++) {
24                 if (prefixSum[i + len][j + len] - prefixSum[i - 1][j + len] - prefixSum[i + len][j - 1] + prefixSum[i - 1][j - 1] <= threshold) {
25                     return len + 1;
26                 }
27             }
28         }
29     }
30 
31     return 0;
32 }

 

Prefix sum implementation

Time Complexity: O(M*N*min(M,N)) where M is row N is col, essentially O(N^3)

Space Complexity: O(M*N) since we need

 

References

• Leetcode discussion solution with binary search and smart solution
• Leetcode discussion normal