第五节：卷积变体

Posted 2023-02-22 快乐江湖

• 相关pdf下载（密码7281）
  

  文章目录

  • 一：空洞卷积
  • 二：分组卷积
  • 三：转置卷积（反卷积）
  • 四：点卷积
  • 五：深度可分离卷积
  • 六：Pytorch实现

一：空洞卷积

空洞卷积（dilated convolution）：又叫做膨胀卷积，在参数不变的情况下，通过添加空洞来扩大感受野

如下图，原本3×3的的卷积核相同参数量和计算量的前提下，通过添加空洞（dilated rate=2）可以使其感受野扩大为5×5

• 普通卷积操作可以认为其dilated rate=1
• 相较于传统卷积操作，以3层3×3卷积为例，如果stride为1，那么最后它只能有7×7的感受野，也就是和层数呈线性关系，但是碰撞卷积的感受野呈现的指数级别的增长

使用空洞卷积时很容易产生“gridding effect”问题。如下，对于layer1来说，当我们连续使用3个膨胀系数为2的空洞卷积时，layer4上的一个pixel利用到layer1上的数据并不是连续的，使得每个非零元素之间存在一定间隔

而如果我们使用的是不同的膨胀系数，就会避免这个问题，例如[1, 2, 3]，此时感受野是连续的

二：分组卷积

分组卷积：分组卷积起源于2012年的AlexNet-（《ImageNet Classification with Deep Convolutional Neural Networks》）。由于当时硬件资源限制，因此作何将特征图分配给多个GPU处理，最后把结果融合

对于普通卷积来说，如果输入特征为（H×W×C），然后应用C^丶个卷积核（每个卷积核大小为h×w×），则输入层会被转化为H^丶×W^丶×C^`的输出特征

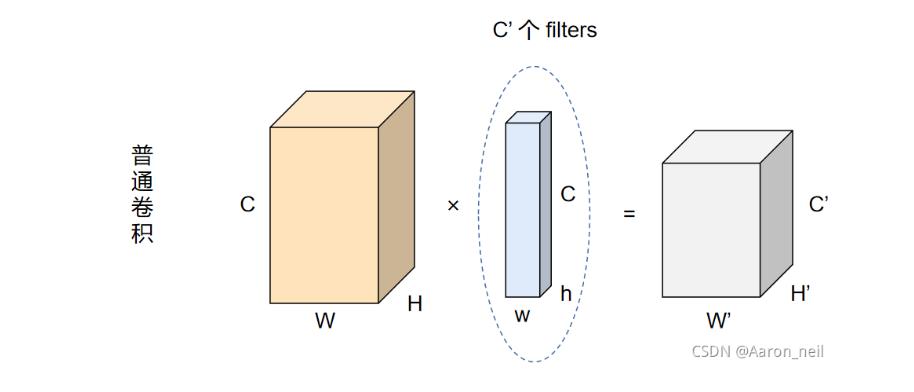
对于分组卷积来说，假设被拆分为两个分组，那么对于没和卷积核组，就包含C^丶/2数量的卷积核，每个卷积核组作用于原来的W×H×C对应通道数一般，也即W×H×C/2，最终每个卷积核组对应输出C^丶/2通道的特征，然后将通道进行堆叠就实现了和普通卷积一样的效果

参数计算

• 对于普通卷积：卷积核为，10×10×3，输出通道为30，即10×10×30
  • 10×10×3×30+30 = 9030parameters
• 对于分组卷积，卷积核为，10×10×3，拆分为3组，则每组为10个10×10×1
  • 10×10×1×10+10=1010parameters，总共3×1010=3030parameters

三：转置卷积（反卷积）

转置卷积直觉感受如下

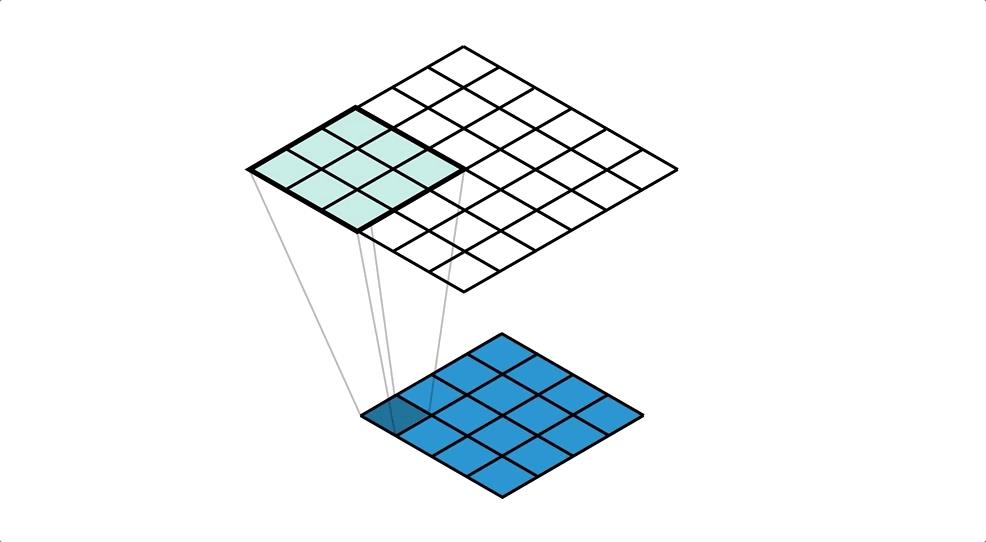
举个例子，将一个4×4的输入通过3×3的卷积核进行普通卷积后，会得到2×2的输出，而转置卷积或反卷积会将一个2×2的输入通过同样3×3的卷积核进行卷积后，得到一个4×4的输出。这听起来像是普通卷积的逆过程，也即反卷积，但事实上这两者没有任何关系。反卷积只能恢复尺寸并不能恢复数值

如下图，在进行反卷积时，将“55”沿着绿色线投影回去，会得到[55, 110, 55]、[110, 55, 110]、[55, 55, 110]，剩余是三个数字亦是如此

我们将得到的四张特征图叠加（对应位置数字相加）后，就得到了反卷积的结果

什么反卷积又被称为转置卷积呢？这是因为反卷积就是将卷积操作中的卷积核进行了转置。如下，之前我们说过卷积操作在框架中是通过矩阵相乘实现的（第四章第三节：卷积层详解2），接着前面的叙述。我们4×16的卷积核进行转置后形成16×4的卷积核，然后与4×1的特征图相乘，分别会形成4个16×1的向量，然后对应位置相加后再reshape即可

反卷积有什么作用呢？具体来说

• 当我们用神经网络生成图片的时候，经常需要将一些低分辨率的图片转换为高分辨率的图片
• 在语义分割中，会使用卷积层在编码器中进行特征提取，然后在解码层中进行恢复为原先的尺寸，这样才可以对原来图像的每个像素都进行分类。这个过程同样需要用到转置卷积

四：点卷积

点卷积：点卷积是一类特殊的卷积运算，其卷积核大小为1×1，主要作用有

• 实现跨通道信息的融合：加入当前层的特征矩阵为224x224x100，而下一层想要得到224x224x50，可以通过1x1的卷积核进行跨通道信息融合，当然这时也可以通过3x3或5x5的卷积核构建出符合下一层224x224x50的特征矩阵，但是使用1x1卷积核，起到了减少参数的目的。
• 实现通道数的升维与降维：本来的通道数为100,而下一层的通道数为50，这时就起到了降维的作用。同理假如下一层的通道数为200，这时就是升维。
• 增加网络的非线性：假如网络本来的通道数为100，而下一层的通道数也是100，这时加入1x1的卷积核并非没有作用，通过1x1卷积核可以增强网络的非线性能力，也可以简单的理解为网络变深了

五：深度可分离卷积

深度可分离卷积等于分组卷积+点卷积，具体来说它会在每个通道上进行点卷积

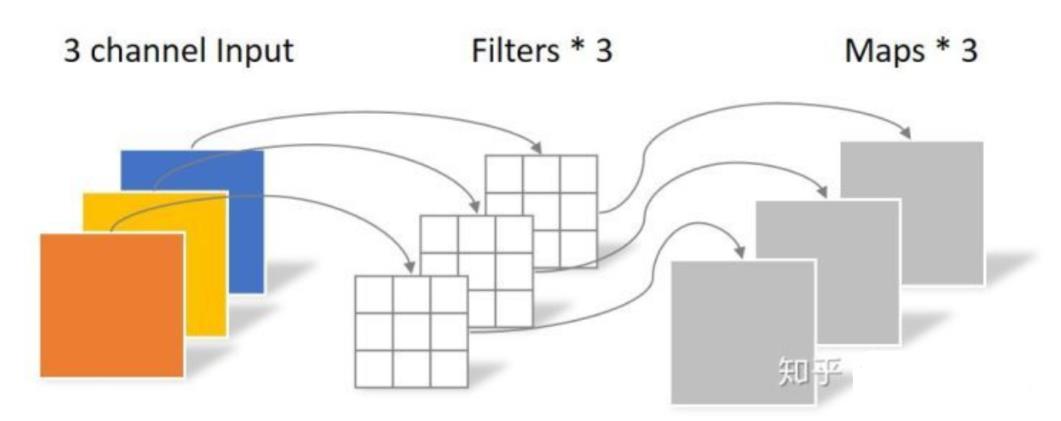
六：Pytorch实现

import torch

# 计算模型所需参数量
def model_para_calc(model):
    sum = 0
    for para in model.parameters():
        # 如果要求梯度追踪
        if para.requires_grad:
            sum += para.numel()
    return sum

# 全连接层
"""
前层：10×10×3 = 300
后层：10×10×30 = 3000
偏置：3000
总和：30×3000+3000 = 903000
"""

model_fc = torch.nn.Linear(in_features=10*10*3, out_features=10*10*30)
print("全连接层所需参数", model_para_calc(model_fc))

# 基本卷积层
"""
(kernel_size_high * kernel_size_width * 通道数 + 1) * 卷积核个数
(10 × 10 * 3 + 1) * 30 = 9030
"""
model_basic_conv2d = torch.nn.Conv2d(in_channels=3, out_channels=30, kernel_size=10, bias=True)
print("卷积层所需参数", model_para_calc(model_basic_conv2d))

# 空洞卷积
"""
设置dilation = (2, 2)，感受野增大，但参数没变
"""
model_dilated_conv2d = torch.nn.Conv2d(in_channels=3, out_channels=30, kernel_size=10, bias=True, dilation=2)
print("空洞卷积所需参数", model_para_calc(model_dilated_conv2d))

# 分组卷积
"""
注意分组数必须设置为in_channels和out_chanels的公约数
(10 × 10 * 1 + 1) * 30 = 3030
"""
model_groups_conv2d = torch.nn.Conv2d(in_channels=3, out_channels=30, kernel_size=10, bias=True, groups=3)
print("分组卷积所需参数", model_para_calc(model_groups_conv2d))

# 点卷积
"""
(1 × 1 × 3 + 1) × 30 = 120
"""
model_pointwise_conv2d = torch.nn.Conv2d(in_channels=3, out_channels=30, kernel_size=1, bias=True)
print("点卷积所需参数", model_para_calc(model_pointwise_conv2d))

# 深度可分离卷积
"""
先分组，然后在每个通道上进行点卷积
(10 × 10 × 1 + 1) × 3 = 303
(1 × 1 × 3 + 1) × 30 = 120
总共120 + 303 = 423
"""

depth_conv2d = torch.nn.Conv2d(in_channels=3, out_channels=3, kernel_size=10, groups=3)
point_conv2d = torch.nn.Conv2d(in_channels=3, out_channels=30, kernel_size=1)
print("深度可分离卷积所需参数", model_para_calc(depth_conv2d) + model_para_calc(point_conv2d) )

结果

全连接层所需参数 903000
卷积层所需参数 9030
空洞卷积所需参数 9030
分组卷积所需参数 3030
分组卷积所需参数 120
深度可分离卷积所需参数 423