力扣leetcode1190. 反转每对括号间的子串

Posted 2021-03-11 Pyrokine

看到已有的题解几乎都是栈操作，但是考虑到leetcode的数据量一直都不大，所以跑一般oj10w长度的字符串很难说栈操作会不会超时，因此尝试生成了10w长度的数据，结果果然效率不够高，因此打算来记录一下笔者的解法

以给的范例"(ed(et(oc))el)"为例，从左到右开始计算，e从1到8，d从2到7，e从3到6再到3……以此类推，发现规律，当存在一层括号时，反转，而反转的目标位置，就是括号首位位置相加然后减去字母所在位置，以第三个字母e为例，(1 + 8) - 3为6，(3 + 6) - 6为3，如果写到一个式子里就是(3 + 6) - [(1 + 8)  - 3]，如果后续再出现括号，以第五个字母o为例，(5 + 6) - {(3 + 6) - [(1 + 8)  - 5]}为6，如果一直在括号内移动，那么只需要改变算式中最后一位数即可，因此可以发现规律，将前面所有式子缓存下来作为基，然后每次加或减最后一位（当前位置的序数），即可得到目标位置

然后考虑如何记录所有括号，使用栈操作和一遍遍历的方式，遇到左括号入栈，遇到右括号出栈，如果长度为0则不记录，同时记录括号的左右位置，然后确定一个定理，最小括号内不会存在更小的括号，证明：该括号是最小括号x1，长度为a1，内部存在括号（反括号），则该括号（反括号）与最小括号x1的反括号（括号）形成括号x2，长度为a2，小于a1，因为括号越小，长度越短，矛盾，因此该括号不是最小括号。因此包含中的最小括号是长度最短的括号，笔者使用list记录括号数量，考虑到后续出栈的效率问题，因此对左括号位置进行一次降序排序，左括号越往前，排在越后面，可以直接出栈，然后在左括号位置相同时，对长度进行升序排列，即先运算外层括号

然后考虑右括号的问题，上面已证明和保证，最后入栈的肯定是最小的且最内层的括号，因此，在计算时，查询当前位置是否有反括号，有则直接出栈，同时根据当前运算符号从基中去除掉

大致运算流程如下图所示

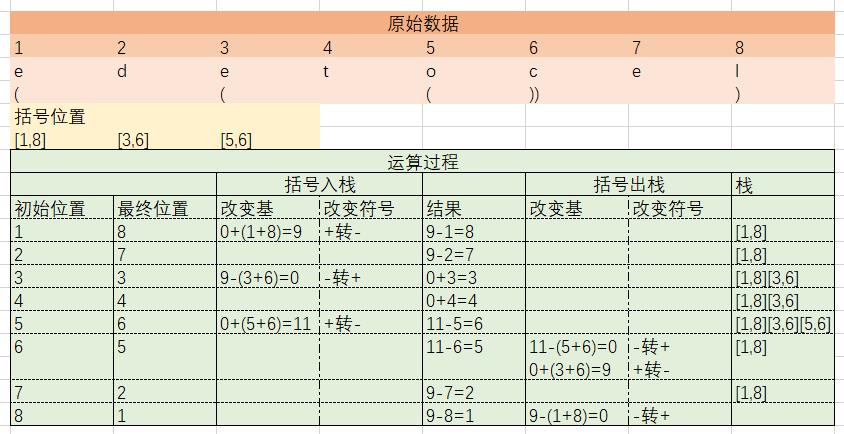
 时间复杂度：两遍遍历，第一遍找到所有括号组合然后排序（sorted是归并排序），第二遍是逐个计算，对比和出栈的时间非常短，因此可以近似为O(n)，实践检验也确实是，以下为三组测试结果，分别对应笔者的算法、标准的栈操作反转和python自带函数[::-1]反转耗时，单位为s

100w字符长度，1w个括号（5k组）

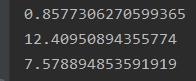
 100w字符长度，10w个括号(5w组)

 

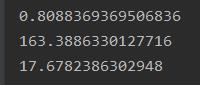
1000w字符长度，10w个括号(5w组)

 

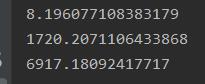
代码如下：

 1 def reverseParentheses(s):
 2     string_list = []
 3     cnt_list = 1
 4     bracket_left = []
 5     bracket_list = []
 6     bracket_list_now = []
 7 
 8     for i in range(0, len(s)):
 9         if \'(\' == s[i]:
10             bracket_left.append(cnt_list)
11         elif \')\' == s[i]:
12             loc_left = bracket_left.pop()
13             loc_right = cnt_list - 1
14             if loc_left < loc_right:
15                 bracket_list.append([loc_left, loc_right, loc_right - loc_left])
16         else:
17             string_list.append(s[i])
18             cnt_list += 1
19     bracket_list = sorted(bracket_list, key=lambda x: (-x[0], x[2]))
20     len_bracket_list = len(bracket_list)
21     calc_base = 0
22     # print(bracket_list)
23     # print(string_list)
24 
25     positive = 1
26     ans = [0 for i in range(len(string_list))]
27 
28     for i in range(0, len(string_list)):
29         if bracket_list:
30             while True:
31                 if bracket_list and i + 1 == bracket_list[len_bracket_list - 1][0]:
32                     if positive:
33                         calc_base += bracket_list[len_bracket_list - 1][0] + bracket_list[len_bracket_list - 1][1]
34                         positive = 1 - positive
35                     else:
36                         calc_base -= bracket_list[len_bracket_list - 1][0] + bracket_list[len_bracket_list - 1][1]
37                         positive = 1 - positive
38                     bracket_list_now.append(bracket_list[len_bracket_list - 1])
39                     bracket_list.pop()
40                     len_bracket_list -= 1
41                 else:
42                     break
43 
44         if positive:
45             ans[calc_base + (i + 1) - 1] = string_list[i]
46         else:
47             ans[calc_base - (i + 1) - 1] = string_list[i]
48 
49         if bracket_list_now:
50             len_bracket_list_now = len(bracket_list_now)
51             j = len_bracket_list_now - 1
52             while j >= 0:
53                 if i + 1 == bracket_list_now[j][1]:
54                     temp = bracket_list_now.pop(j)
55                     if positive:
56                         calc_base += temp[0] + temp[1]
57                         positive = 1 - positive
58                     else:
59                         calc_base -= temp[0] + temp[1]
60                         positive = 1 - positive
61                     len_bracket_list_now -= 1
62                     j -= 1
63                 else:
64                     break
65     # return ans
66     return "".join(ans)
67 
68 
69 def reverseParentheses2(s):
70     while \'(\' in s:
71         s = re.sub(r\'\\(([^()]*)\\)\', lambda x: x.group(1)[::-1], s)
72     return s
73 
74 
75 def reverseParentheses3(s):
76     ans = [\'\']
77     for c in s:
78         if c == \'(\':
79             ans += [\'\']
80         elif c == \')\':
81             ans[-2] += ans[-1][:: -1]
82             ans.pop()
83         else:
84             ans[-1] += c
85     return ans[0]

如有错误，欢迎指正！