CF 999E Reachability from the Capital

Posted 2021-03-06 chinesepikaync

题意：

题目描述

在 Berland 有 (n) 座城市和 (m) 条道路，每条道路连接着一对城市。

Berland 的道路都是单向的

为了能让首都能够到达所有的城市，最少需要新修建多少新道路？

新道路也是单向的

输入格式

输入的第一行包含三个整数 (n,m) 和 (s) ((1le n le 5000,0le m le 5000 , 1le s le n)) ——城市数，道路数和首都所在城市的标号。 城市的标号为 (1) ~ (n)
接下来 (m) 行每行包含一条道路连接着一对城市 (u_i,v_i) ((1le u_i,v_ile n,u_i e v_i))

对于每对城市 (u,v)，从 (u) 到 (v) 最多只能有一条道路。 允许在一对城市之间建造相反方向的道路（即从 (u) 到 (v) 和从 (v) 到 (u) ）。

输出格式

输出一个整数——使从首都可以到达所有城市所需的最少新修建道路数。如果从 (s) 已经可以到达所有城市，则输出 (0)。

说明/提示

样例 1：

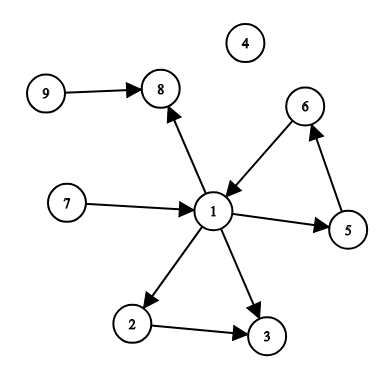
例如，您可以添加道路 ( 6, 4 ) , ( 7 , 9 ) , ( 1 , 7 )，以使从 (s = 1) 可到达所有城市。
样例 2：

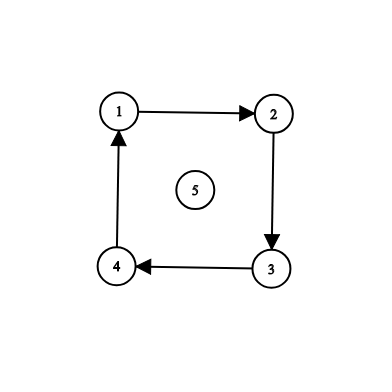
在此样例中，您可以添加道路（5 , 1），（5 , 2），（5 , 3），（5 , 4）中的任何一条，以使可从 (s = 5) 到达所有城市。

---

如果一个强连通分量内的一个点能被 (s) 到达，那么强连通分量里所有点都被 (s) 到达，所以先缩点

缩完点建完新图，我们看到的基本上就只有这么三种情况的连通块

A -> B -> D       E -> F -> G        H -> I -> J
     ^                                    |
     |                                    V
     C                                    K

我们假设这三种情况都不能被 (s) 到达

第一种多个入度为0的点，必须要从 (s) 往 (A) 和 (C) 各连一条边才行

第二种一条链，(s) 往 (E) 连边就行

第三种只有一个入度为 0 的点，那么 (s) 往 (H) 连边就行

那么这里就发现了规律了，对于一个不能被 (s) 所到达的连通块，其所要新加边的数量为其中入度为 0 点的数量

那么就在新图中先从 (s) 所在新图中的点开始 dfs 一遍标记掉能到达的点

然后答案就是新图中没被标记过并且入度为 0 的点数

// This code writed by chtholly_micromaker(MicroMaker)
#include <bits/stdc++.h>
#define reg register
using namespace std;
const int MaxN=5050;
struct Edge
{
    int nxt,to;
}E[MaxN<<2],nE[MaxN<<2];
template <class t> inline void read(t &s)
{
    s=0;
    reg int f=1;
    reg char c=getchar();
    while(!isdigit(c))
    {
        if(c=='-')
            f=-1;
        c=getchar();
    }
    while(isdigit(c))
        s=(s<<3)+(s<<1)+(c^48),c=getchar();
    s*=f;
    return;
}
int hd[MaxN],nhd[MaxN],en,nen,n,m;
int dfn[MaxN],low[MaxN],dep;
int col[MaxN],scc;
int sta[MaxN],top;
bool instack[MaxN];
bool vis[MaxN];
int deg[MaxN];
inline void adde(int u,int v)
{
    ++en;
    E[en]=(Edge){hd[u],v};
    hd[u]=en;
    return;
}
inline void nadde(int u,int v)
{
    ++nen;
    nE[nen]=(Edge){nhd[u],v};
    nhd[u]=nen;
    return;
}
inline void tarjan(int u)
{
    dfn[u]=low[u]=++dep;
    sta[top++]=u;
    instack[u]=true;
    for(int i=hd[u];~i;i=E[i].nxt)
    {
        reg int v=E[i].to;
        if(!dfn[v])
        {
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }
        else if(instack[v])
            low[u]=min(low[u],dfn[v]);
    }
    if(dfn[u]==low[u])
    {
        ++scc;
        do
        {
            --top;
            instack[sta[top]]=false;
            col[sta[top]]=scc;
        }while(sta[top]!=u);
    }
    return;
}
inline void dfs(int u,int fa)
{
    vis[u]=true;
    for(int i=nhd[u];~i;i=nE[i].nxt)
    {
        reg int v=nE[i].to;
        if(v==fa||vis[v])
            continue;
        dfs(v,u);
    }
    return;
}
signed main(void)
{
    memset(hd,-1,sizeof hd);
    memset(nhd,-1,sizeof nhd);
    int s;
    reg int u,v;
    cin>>n>>m>>s;
    for(int i=1;i<=m;++i)
    {
        read(u);read(v);
        adde(u,v);
    }
    for(int i=1;i<=n;++i)
        if(!dfn[i])
            tarjan(i);
    for(int u=1;u<=n;++u)
        for(int i=hd[u];~i;i=E[i].nxt)
        {
            reg int v=E[i].to;
            if(col[u]==col[v])
                continue;
            nadde(col[u],col[v]);
            ++deg[col[v]];
        }
    dfs(col[s],0);
    reg int ans=0;
    for(int i=1;i<=scc;++i)
        if(!vis[i]&&!deg[i])
            ++ans;
    cout<<ans<<endl;
    return 0;
}