给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
- 所有数字(包括 target)都是正整数。
- 解集不能包含重复的组合。
示例 1:
输入: candidates = [2,3,6,7], target = 7,
所求解集为:
[
[7],
[2,2,3]
]
这一题乍一看还是挺简单的,但是还是需要注意一些细节
去掉重复元素
一个比较重要的问题就是怎么去掉重复的元素,我们拿这样一张图理解一下,图中画的是candidates=[2,3,6,7]时它的组合树的第二、三层
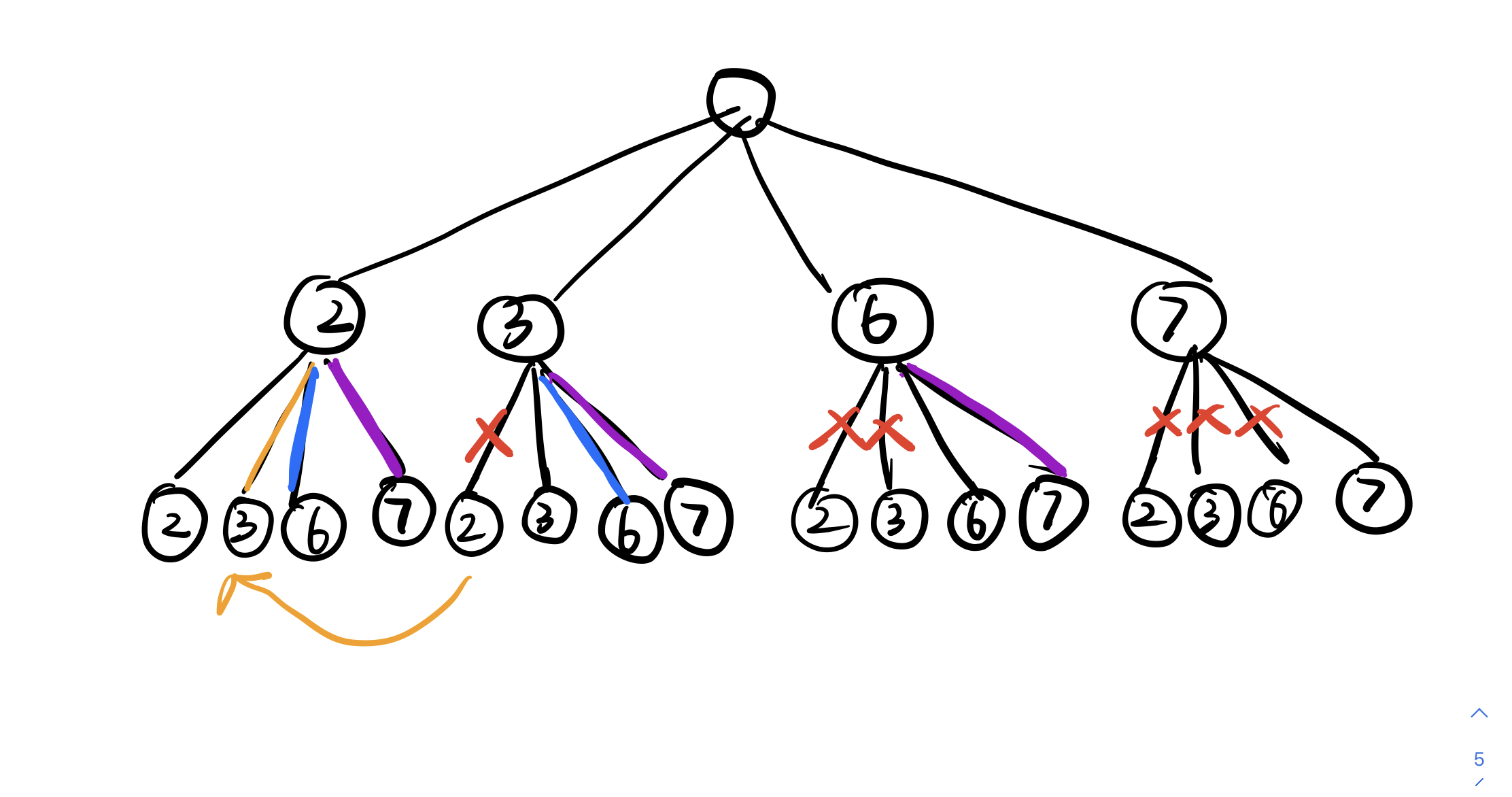
我们可以发现,其实有一些节点是不必要的,正如其中被红色叉去掉的边。举个例子,对于第二层的节点3来说,它的儿子节点2是不必要的,为什么呢,它和它的儿子2组合得到的结果是[3,2],但是[3,2]这个组合,不考虑顺序的话其实已经在第二层节点2中出现过了,这就有点像我们考虑顺序的排列组合A几几和不考虑顺序的排列组合C几几的区别,不考虑顺序的话实际只有n!个结果。
再拿一个简单例子来说,假如有数字集合{1,2,3},我们需要不考虑顺序的两两组合,问有哪些情况,我们如果从前向后推,就会推得组合{1,2},{1,3},{2,3},为什么我们不会去再继续下去选择{2,1}就是这样的道理(听起来有点牵强)。
总之我们就得到了在排列组合的过程中,下一层的节点只需要从这一层的索引开始遍历即可,即对于3,索引是1,索引即索引之后就是3,6,7。
其他一些细节
同时在提交结果的时候,我还发现了细微了一些不同。
我的其中一次代码如下
class Solution {
private:
vector<int> temp;
public:
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
vector<vector<int>> result;
sort(candidates.begin(), candidates.end());
// this->target = target;
searchNums(target, candidates, result, 0);
return result;
}
void searchNums(int target, vector<int> & candidates, vector<vector<int>>& result, int start){
if(target < 0){ //注意!
return;
}
if(target == 0){
result.push_back(temp);
return;
}
for(int i = start; i < candidates.size(); i++){
temp.push_back(candidates[i]);
searchNums(target-candidates[i], candidates, result, i);
temp.pop_back();
}
}
};
执行结果:12ms 7.7MB
但当我稍作修改,改为如下代码
class Solution {
private:
vector<int> temp;
public:
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
vector<vector<int>> result;
sort(candidates.begin(), candidates.end());
searchNums(target, candidates, result, 0);
return result;
}
void searchNums(int target, vector<int> & candidates, vector<vector<int>>& result, int start){
if(target == 0){
result.push_back(temp);
return;
}
for(int i = start; i < candidates.size() && target-candidates[i] >= 0; i++){ //注意!
temp.push_back(candidates[i]);
searchNums(target-candidates[i], candidates, result, i);
temp.pop_back();
}
}
};
执行结果: 4ms 7.6MB
其实这两个情况就只有终止的判断不同,一个是在新一次的递归开始之时,一个是在新一次递归开始之前
if(target < 0){ //注意!
return;
}
target-candidates[i] >= 0;
当你仔细分析一下,就会发现其实在新的一次递归开始判断是没有意义且浪费空间的,因为在开始一次新的调用的时候需要进行相关的准备,包括保持旧的调用的状态以供返回现场,还要为新的栈开辟空间,结果刚开始新的一轮调用就结束了。这就好像父母辛辛苦苦准备了一桌大餐,结果你说,这个菜我不喜欢吃(条件不满足),就不吃了,这不是明摆着浪费么······
所以说,在做题训练的时候也千万不要忘记细节啊qwq