LeetCode编程训练 - 回溯(Backtracking)

Posted 2021-02-16 bangerlee

回溯基础

先看一个使用回溯方法求集合子集的例子(78. Subsets)，以下代码基本说明了回溯使用的基本框架：

//78. Subsets
class Solution {
private:
    void backtrack(vector<vector<int>>& res,vector<int>& tmp,vector<int>& nums,int start){
        res.push_back(tmp);    //满足一定条件下将当前数据加入结果集
        for(int i=start;i<nums.size();i++){
            tmp.push_back(nums[i]);    //选择一条路径
            backtrack(res,tmp,nums,i+1);    //DFS朝当前路径行进
            tmp.pop_back();    //回退路径
        }
    }
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        vector<vector<int>> res;
        vector<int> tmp;
        backtrack(res,tmp,nums,0);
        return res;
    }
};

 

即回溯方法主要有以下四个步骤：

1. 满足一定条件下将当前数据加入结果集
    (或检查到不满足要求当即返回)
2. 选择一条路径
3. DFS向前进行
4. 回退路径

一些情况下需要对数据进行预先处理，或在第2步直接检查以决定是否抛弃当前路径，以避免过多地递归、带来时间损耗。换而言之，不满足条件的路径越早抛弃越好。

 

理解回溯

回溯方法用到递归，涉及到递归让我们理解起来就不那么直观。下图直观展示了以上Subsets求解代码的执行过程，第5步开始出现路径回退：

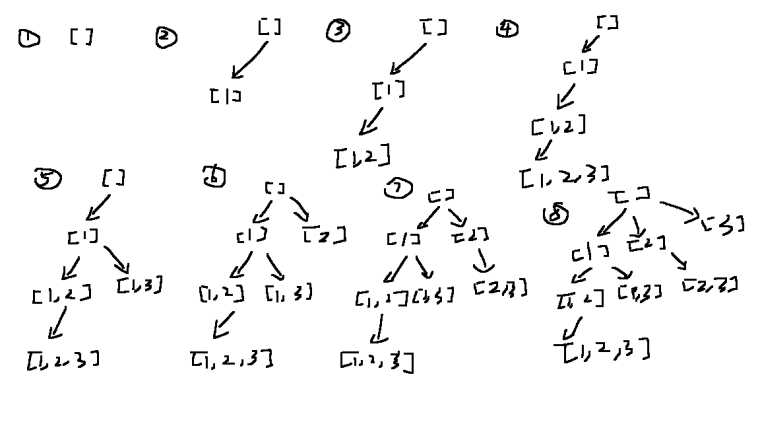
可以把回溯的执行理解为一颗树从根到叶、从左到右的展开过程。图片来源 这里

 

回溯时间复杂度

同样因为用到递归，时间复杂度亦不能够直观地计算，以上Subsets问题比较容易地能看出来为O(2^n)。如果对递归过程计算时间复杂度，详见 这里

 

相关LeetCode题：

78. Subsets  题解 

90. Subsets II  题解

22. Generate Parentheses  题解

46. Permutations  题解

47. Permutations II  题解

79. Word Search  题解

39. Combination Sum  题解

40. Combination Sum II  题解

37. Sudoku Solver  题解

51. N-Queens  题解  可视化